Solving 3 Equations for 3 Unknowns Using a Matrix in Row Echelon Form

Dr. Pierce's Physics & Math

8 Jun 202110:17

EducationalLearning

32 Likes 10 Comments

TLDRThe video script presents a step-by-step guide on solving a system of three linear equations with three unknowns using the method of reducing a matrix to row echelon form. The process involves manipulating the coefficients of the variables to create a matrix, performing row operations to achieve zeros at the bottom, and then back-substituting to find the values of the variables. The example provided leads to the solution x = -1, y = -2, and z = 1, demonstrating a clear and methodical approach to solving such algebraic problems.

Takeaways

📝 The script explains an algorithm for solving a system of three linear equations with three unknowns (x, y, z).
🔢 The process involves creating a matrix with coefficients of the variables and constants from the equations.
🌟 The algorithm simplifies the matrix through a series of row operations, including scalar multiplication and addition of rows.
🎯 The goal of row operations is to get zeros in the bottom row of the matrix, which simplifies the equations for easier variable resolution.
🔄 The first row operation is to eliminate the first variable (x) from the second and third equations.
🔄 The second operation is to eliminate the second variable (y) from the third equation.
🔄 Further row operations are performed to isolate the remaining variables and solve for their values.
📌 The script demonstrates that by solving the simplified equations, the values of z, y, and x can be determined in sequence.
👉 The final solution to the example given is x = -1, y = -2, and z = 1.
📚 The method used is known as reducing the matrix to row echelon form, which is a key technique in linear algebra for solving systems of equations.

Q & A

What is the main topic of the transcript?
-The main topic of the transcript is solving a system of three linear equations with three unknowns using an algorithm.
What are the three variables in the equations discussed in the transcript?
-The three variables in the equations are x, y, and z.
How does the algorithm begin to simplify the system of equations?
-The algorithm begins by peeling off the coefficients of the variables, creating a shorthand for multiplying a matrix by the variables x, y, and z.
What are the operations allowed on the rows of the matrix according to the transcript?
-The operations allowed on the rows of the matrix include multiplying a row by a scalar, adding any two rows together, and multiplying a row by a constant.
What is the goal of performing these operations on the matrix?
-The goal is to get the three numbers in the bottom corner of the matrix to be zeros, which makes it easier to solve for the variables.
How does the process of getting zeros in the bottom corner help in finding the values of the variables?
-Once the matrix is in reduced row echelon form with zeros in the bottom corner, the equations become simpler, allowing for direct calculation of the variable values by substitution and elimination.
What is the value of z determined from the bottom equation of the simplified matrix?
-The value of z is determined to be 1 from the bottom equation of the simplified matrix.
How is the value of y found after finding the value of z?
-The value of y is found by substituting the value of z into the equation above it, which simplifies to -6y - 1 = 11, resulting in y being -2.
What is the final value of x after determining the values of y and z?
-After substituting the values of y and z into the top equation, x is found to be -1.
What is the solution to the original system of equations as discussed in the transcript?
-The solution to the original system of equations is x = -1, y = -2, and z = 1.
Why is the reduced row echelon form useful in solving systems of linear equations?
-The reduced row echelon form is useful because it simplifies the system of equations, making it easier to identify the relationships between the variables and thus find their values more efficiently.

Outlines

00:00

📚 Introduction to Solving a System of Three Equations

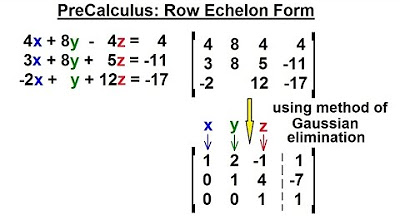
This paragraph introduces the观众 to the process of solving a system of three linear equations with three unknowns, x, y, and z. The speaker explains an algorithm that involves manipulating the coefficients of the variables to form a matrix, which is then used to represent the system in a shorthand form. The goal is to simplify the matrix into a form where the bottom row contains zeros, which makes it easier to solve for the variables. The speaker demonstrates the initial steps of this process, including multiplying and adding equations to manipulate the coefficients.

05:01

🔍 Matrix Manipulation for Zeroing Variables

In this paragraph, the speaker continues the process of matrix manipulation by focusing on getting zeros for the variables in the bottom row of the matrix. The speaker uses scalar multiplication and addition of equations to achieve this. The process involves a series of steps, including multiplying the first equation by -2 and adding it to the second, and multiplying the third equation by -3 and adding it to the first, to eliminate the unwanted coefficients. This leads to a matrix in reduced row echelon form, which simplifies the process of solving for the variables.

10:01

🎓 Solving for x, y, and z

The final paragraph focuses on solving for the variables x, y, and z using the simplified matrix from the previous steps. The speaker explains that the bottom row of the matrix, which now contains a single non-zero value, directly gives the value of z as 1. Using this information, the speaker back-substitutes into the other equations to find the values of y and x. The process involves solving the second equation to find y = -2 and the first equation to find x = -1. The paragraph concludes with the solution to the original system of equations, which is x = -1, y = -2, and z = 1.

Mindmap

Keywords

💡Algorithm

An algorithm is a step-by-step procedure for solving a specific problem, often in mathematics or computer science. In the context of the video, the algorithm refers to a method for solving a system of three linear equations with three unknowns, which is crucial for understanding how to find the values of the variables x, y, and z.

💡Independent Equations

Independent equations are mathematical statements where each one provides unique information, rather than being a repetition or consequence of the others. In the video, the three given equations for the variables x, y, and z are independent, meaning they are necessary to find a unique solution for each variable.

💡Coefficients

Coefficients are numerical factors that multiply variables in an equation or function. They determine the magnitude or degree to which the variable affects the outcome. In the video, the coefficients are the numbers before the variables x, y, and z in each equation.

💡Matrix

A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. In mathematics and computer science, matrices are used to represent data and to perform operations on them, such as multiplication and addition. In the video, the concept of a matrix is used to represent the system of equations in a shorthand form.

💡Scalar

A scalar is a quantity that has magnitude but no direction. In the context of the video, multiplying an equation by a scalar means multiplying every term in the equation by the same non-zero number to maintain the equality. This operation is one of the steps in the algorithm for solving the system of equations.

💡Reduce Row Echelon Form

Reduce Row Echelon Form (RREF) is a specific way of writing a system of linear equations that makes it easier to find the solution. It involves transforming the matrix into a form where the bottom rows contain only zeros, and the nonzero rows have a leading coefficient (the first non-zero number from the left, called the leading entry) of 1.

💡Variables

Variables are symbols, often letters like x, y, and z, that represent unknown quantities in a mathematical equation or expression. In the video, the variables x, y, and z are the unknowns that the algorithm aims to solve for.

💡Linear Equations

Linear equations are mathematical equations in which the highest power of the variables is one. They represent straight lines when graphed and are fundamental in algebra. The video's main theme involves solving a system of three linear equations with three unknown variables.

💡Shorthand

Shorthand is a way of writing or representing something in a more concise form, often used to save time or space. In the video, shorthand is used to represent the system of equations in a more compact form, making it easier to manipulate and solve.

💡Solving Equations

Solving equations refers to the process of finding the values of the variables that make the equation true. In the video, the focus is on solving a system of three linear equations to find the values of x, y, and z that satisfy all three equations simultaneously.

💡Leading Entry

The leading entry in a matrix, particularly in the context of row echelon form, is the first non-zero entry from the left in a row. Ensuring that each row has a leading entry of 1 is part of the process of reducing the matrix to solve the system of linear equations.

Highlights

The introduction of an algorithm for solving a system of three equations with three unknowns. (Start time: beginning)

The concept of independent equations and variables x, y, and z. (Start time: 3 seconds)

Peeling off coefficients to simplify the equations. (Start time: 7 seconds)

The use of matrix multiplication as a shorthand for the equations. (Start time: 10 seconds)

The explanation of how to manipulate the rows of the matrix. (Start time: 15 seconds)

The goal of reducing the bottom three numbers to zeros. (Start time: 20 seconds)

The process of making the bottom corner zeros by multiplying and adding rows. (Start time: 25 seconds)

The explanation of how to get the value of z from the third equation. (Start time: 30 seconds)

The method for finding the value of y using the second equation. (Start time: 35 seconds)

The process of solving for x using the first equation and the known values of y and z. (Start time: 40 seconds)

The final solution for the system of equations: x = -1, y = -2, and z = 1. (Start time: 45 seconds)

The explanation of the reduce row echelon form and its significance. (Start time: 50 seconds)

The practical application of the algorithm in solving real-world problems. (Start time: 55 seconds)

The use of scalar multiplication and addition of equations as a method for solving the system. (Start time: 1 minute)

The step-by-step breakdown of the algorithm, making it accessible for learners. (Start time: 1 minute 5 seconds)

The importance of understanding the variables and coefficients in the context of the equations. (Start time: 1 minute 10 seconds)

The demonstration of how to use the reduced form to quickly identify the values of the variables. (Start time: 1 minute 15 seconds)

The emphasis on the role of the algorithm in simplifying complex mathematical problems. (Start time: 1 minute 20 seconds)

Transcripts

Browse More Related Video

PreCalculus - Matrices & Matrix Applications (5 of 33) Method of Gaussian Elimination: Example

Gaussian Elimination With 4 Variables Using Elementary Row Operations With Matrices

PreCalculus - Matrices & Matrix Applications (10 of 33) Gaussian Elimination: Example of Solving 3x3

Matrices: Reduced row echelon form 2 | Vectors and spaces | Linear Algebra | Khan Academy

PreCalculus - Matrices & Matrix Applications (3 of 33) Row Echelon Form

Gauss Jordan Elimination & Reduced Row Echelon Form

Solving 3 Equations for 3 Unknowns Using a Matrix in Row Echelon Form

Takeaways

Q & A

What is the main topic of the transcript?

What are the three variables in the equations discussed in the transcript?

How does the algorithm begin to simplify the system of equations?

What are the operations allowed on the rows of the matrix according to the transcript?

What is the goal of performing these operations on the matrix?

How does the process of getting zeros in the bottom corner help in finding the values of the variables?

What is the value of z determined from the bottom equation of the simplified matrix?

How is the value of y found after finding the value of z?

What is the final value of x after determining the values of y and z?

What is the solution to the original system of equations as discussed in the transcript?

Why is the reduced row echelon form useful in solving systems of linear equations?