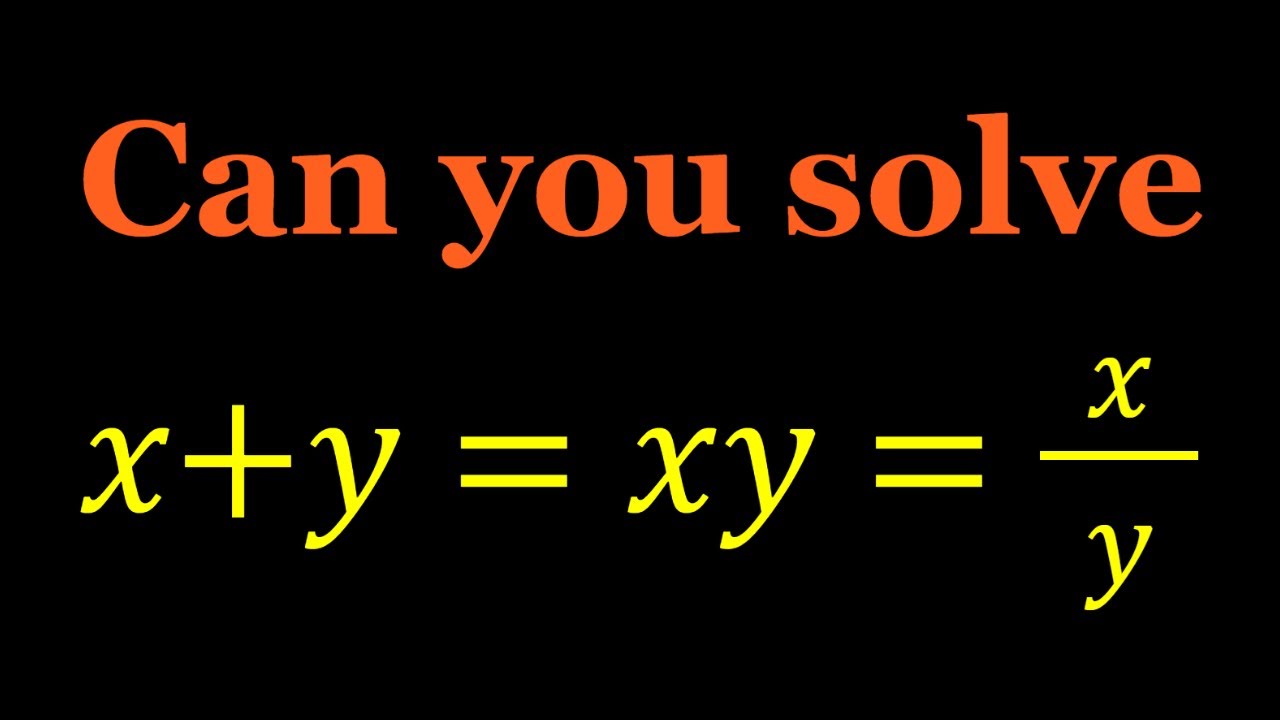Radical equation | Radical simplification | math tricks |Math Olympiad | unique math tricks

Ordy loves math
11 Mar 202408:33
EducationalLearning
32 Likes 10 Comments

TLDRIn this engaging video, the presenter tackles the challenge of solving a complex equation involving rational numbers and radicals. By squaring both sides of the equation and carefully manipulating the terms, the video demonstrates the process of isolating variables and forming a system of equations. The presenter arrives at two potential solutions, (x, y) = (32/2, 1/2) and (1/2, 32), but only the first pair satisfies the original inequality, making it the correct solution. The video is an excellent example of mathematical problem-solving and encourages viewers to subscribe for more content.

Takeaways
  • 📌 The video begins with a call to action for viewers to support the channel by subscribing.
  • 🔢 The main goal is to find a pair of rational numbers X and Y that satisfy a given equation involving square roots.
  • 💡 The strategy involves squaring both sides of the equation to eliminate the radicals.
  • 📈 After squaring, the equation is transformed into a system of two quadratic equations: x < tk3 + y < tk3 and x + y = 2.
  • 🤔 The video emphasizes that since X and Y are rational, their sum must also be rational, leading to x + y = 2.
  • 🧩 The equation is rearranged to isolate terms and simplify the system: 2 - <TK3 * <TK3 = x + y - 2 root.
  • 🔍 The video demonstrates the process of solving a quadratic equation using the quadratic formula: x = (-b ± √(b² - 4ac)) / (2a).
  • 📊 Two solutions for X are found: x = 3/2 and x = -1/2, which correspond to two possible pairs of (X, Y).
  • 🔎 The video concludes by checking the solutions against the original equation to ensure they are valid.
  • 🎉 The final valid solution provided is X = 3/2 and Y = -1/2, satisfying the original equation.
  • 🙏 The video ends with a reminder for viewers to subscribe to the channel for more content.
Q & A

  • What is the main objective of the video?

    -The main objective of the video is to solve for the pair of rational numbers X and Y that satisfy a given equation involving square roots.

  • How does the video start the process of solving the equation?

    -The video begins by squaring both sides of the equation to eliminate the square root, resulting in a quadratic equation.

  • What is the initial equation the video is trying to solve?

    -The initial equation is √(2) < √(k3 - 3) on the left side and √(X) < √(k3) - √(Y) on the right side.

  • What is the significance of squaring both sides of the equation?

    -Squaring both sides is a common algebraic technique used to eliminate square roots and simplify the equation.

  • What are the two equations that form the system after squaring and rearranging?

    -The two equations are x + y = 2 and √(3) * √(x) = √(y).

  • How does the video solve for X and Y?

    -The video sets up a system of two equations, then solves for Y in terms of X using one equation, and substitutes this into the other to solve for X.

  • What is the quadratic equation derived from the system?

    -The quadratic equation derived is 4x^2 - x + 3 = 0.

  • What are the two solutions for X found in the video?

    -The two solutions for X are x = 3/2 and x = -3/2.

  • What are the corresponding values for Y when X is 3/2 and -3/2?

    -When X is 3/2, Y is -1/2, and when X is -3/2, Y is 5/2.

  • Which pair of (X, Y) is the correct solution according to the video?

    -The correct solution is (X, Y) = (3/2, -1/2) or (3/2, 1/2).

  • How does the video verify the solution?

    -The video verifies the solution by substituting the values back into the original equation and showing that they satisfy the inequality.

Outlines
00:00
📚 Introduction and Problem Statement

The speaker begins by welcoming the audience back to their channel and introduces the topic of solving a mathematical problem involving rational numbers and radicals. They request support in the form of subscriptions and express gratitude to existing subscribers. The problem at hand is to find a pair of rational numbers (X, Y) that satisfy a given equation. The speaker then proceeds to explain their approach, which involves squaring both sides of the equation to eliminate the radical. The process is detailed, including the algebraic manipulations and the resulting equations.

05:03
🧠 Solving the Quadratic Equation

In this segment, the speaker continues to work through the problem, focusing on solving the quadratic equation derived from the previous steps. They apply the quadratic formula to find the values of x, and then use these to determine the corresponding values of y. The speaker presents two potential solutions for the pair (x, y), which are rational numbers as required by the problem's conditions. They conclude by verifying these solutions against the original equation and encourage viewers to subscribe to their channel for more content.

Mindmap
Keywords
💡Rational Numbers
Rational numbers are a category of numbers that can be expressed as the quotient or fraction of two integers, where the denominator is not zero. In the context of the video, the host is seeking a pair of rational numbers (X and Y) that satisfy a given equation, emphasizing that both X and Y must be rational for their sum and product to also be rational.
💡Square Roots
Square roots are the mathematical operation that finds the value which, when multiplied by itself, gives the original number. In the video, the host uses the concept of square roots to simplify the equation by eliminating radicals and later to solve for the variables X and Y.
💡Squaring
Squaring is the process of multiplying a number by itself. In the video, squaring is used as a technique to eliminate square roots from the equation, which simplifies the process of finding the rational numbers that satisfy the given equation.
💡Equations
Equations are mathematical statements that assert the equality of two expressions. In the video, the equation involves square roots and the goal is to find values for X and Y that make the equation true.
💡Subscription
A subscription, in the context of the video, refers to the viewer's support for the content creator by signing up to receive ongoing content, typically on platforms like YouTube. The host asks viewers to subscribe to their channel as a form of encouragement and support for their work.
💡Channel
In the context of online content platforms, a channel is a user's personal page or profile where they can upload and share their content, such as videos. The host mentions their channel in relation to seeking support through subscriptions.
💡Radicals
Radicals, in mathematics, often refer to the root symbols used in algebraic expressions, such as the square root symbol (√). In the video, the host aims to eliminate radicals from the equation by squaring both sides.
💡Factoring
Factoring is the process of breaking down a mathematical expression into its simplest components, often by finding common factors. In the video, the host factors out a common term from both sides of the equation to simplify the process of solving for X and Y.
💡Quadratic Equation
A quadratic equation is a polynomial equation of degree two, typically in the form ax² + bx + c = 0. In the video, the host ends up with a quadratic equation in one variable after simplifying the original equation involving X and Y.
💡Solving Equations
Solving equations involves finding the values of the variables that make the equation true. The video demonstrates a step-by-step process of solving a system of equations involving rational numbers and square roots.
💡Systems of Equations
A system of equations is a set of two or more equations that are solved simultaneously. In the video, the host starts with a single equation and through algebraic manipulation, ends up with a system of two equations involving X and Y.
Highlights

The video begins with an introduction to solving a radical equation involving rational numbers X and Y.

The goal is to find a pair of rational numbers (X, Y) that satisfy a given equation.

The channel owner asks for support by encouraging viewers to subscribe to the channel.

The method starts by squaring both sides of the equation to eliminate the radical.

After squaring, the equation is transformed into a quadratic equation involving X and Y.

The video demonstrates the process of simplifying the equation by factoring out terms.

The video identifies that X + Y must be a rational number equal to 2 based on the equation.

A system of two equations is formed, which is then solved for Y in terms of X.

The video shows the process of solving a quadratic equation using the quadratic formula.

Two potential solutions for X are found, which are then used to find corresponding Y values.

The video concludes with two pairs of (X, Y) that satisfy the original equation.

The first pair identified is (X, Y) = (32, 1/2) and the second pair is (X, Y) = (1, 12).

The video emphasizes the importance of X being greater than Y based on the original equation.

The final solution is confirmed to be X * Y = 32 1/2, which is a rational number pair.

The video ends with a call to action for viewers to subscribe and a teaser for the next video.

Transcripts

Browse More Related Video

Solving a System Equations | #Algebra

Solving Quadratic Equations With Exponents

Let's Solve An Interesting Differential Equation

Word Problem in Maths.

Separable First Order Differential Equations - Basic Introduction

Logarithmic Equations

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Radical EquationsMathematics TutorialRational NumbersStep-by-Step SolutionEducational ContentMath ChannelSubscription RequestEngaging HostQuadratic EquationsMathematics Enthusiasts