Solving Systems of Equations By Graphing

The Organic Chemistry Tutor
18 Jan 201805:14
EducationalLearning
32 Likes 10 Comments

TLDRThis video lesson demonstrates how to solve a system of linear equations by graphing. The instructor begins by presenting two equations: y = 2x - 3 and y = -2/3x + 5. The process involves graphing both equations on a large coordinate plane to clearly identify the point of intersection, which represents the solution to the system. The first equation is graphed using its slope of 2 and y-intercept of -3, while the second is graphed with a slope of -2/3 and y-intercept of 5. The intersection point, (3,3), is found and verified by substituting the values back into the original equations. The lesson emphasizes the importance of a clear, large graph for accurate solutions and concludes with a substitution method to confirm the graphical solution.

Takeaways
  • 📚 The lesson is about solving a system of linear equations by graphing.
  • 📈 The first equation is in slope-intercept form: \( y = 2x - 3 \).
  • 📊 The second equation is also in slope-intercept form: \( y = -\frac{2}{3}x + 5 \).
  • 📍 The solution to the system is the point of intersection of the two graphs.
  • 🔍 A large graph is recommended for clarity in identifying the solution.
  • 📐 The slope of the first equation is 2, and the y-intercept is -3.
  • 📏 For the second equation, the slope is \( -\frac{2}{3} \), and the y-intercept is 5.
  • 📝 Graphing involves plotting points using the slope and y-intercept for each equation.
  • 🔢 The point of intersection is found to be (3, 3) by graphing.
  • 🔄 The solution is verified by substituting \( y = 2x - 3 \) into the second equation.
  • 🧮 The substitution method leads to solving for \( x \) and then \( y \), confirming the solution (3, 3).
Q & A

  • What is the method used in this lesson to solve a system of equations?

    -The method used to solve the system of equations in this lesson is graphing.

  • What are the two equations given in the lesson?

    -The two equations given are y = 2x - 3 and y = -2/(3x) + 5.

  • What is the advantage of drawing a large graph when solving equations by graphing?

    -The advantage of drawing a large graph is that it makes it easier to clearly see where the solution is going to be. If the graph has marks closely spaced, it might be difficult to see the answer.

  • What is the slope and y-intercept of the first equation?

    -The slope of the first equation is 2, and the y-intercept is -3.

  • How do you find the next point on the graph for the first equation?

    -To find the next point, use the slope which is rise over run. Go up two units and travel one unit to the right from the y-intercept.

  • What is the y-intercept of the second equation?

    -The y-intercept of the second equation is 5.

  • What is the slope of the second equation and how does it affect the graphing process?

    -The slope of the second equation is -2/3. This means for every three units you travel to the right, you go down two units on the graph.

  • How do you determine the point of intersection between the two graphs?

    -The point of intersection is found by graphing both equations and identifying the point where the lines cross on the graph. In this case, it is the point (3,3).

  • What is the solution to the system of equations as found by graphing?

    -The solution to the system of equations, as found by graphing, is the point (3,3).

  • How is the solution verified using substitution?

    -The solution is verified by substituting y with 2x - 3 in the second equation and solving for x. After finding x = 3, substitute it back into one of the original equations to find y, which also equals 3, confirming the solution (3,3).

  • What is the purpose of multiplying through by 3 in the substitution method to eliminate the fraction?

    -Multiplying through by 3 is done to eliminate the fraction in the equation, making it easier to solve for x by clearing the denominator.

Outlines
00:00
📚 Solving Systems of Equations by Graphing

This paragraph introduces a lesson on solving systems of equations using the graphing method. The instructor presents two equations: the first is linear (y = 2x - 3) and the second is rational (y = -2/(3x) + 5). The objective is to graph both equations and find their point of intersection, which represents the solution to the system. The instructor emphasizes the importance of drawing a large graph for clarity and begins by marking the y-axis at 5 and similarly for the x-axis. The process involves identifying the slope and y-intercept for each equation and plotting points accordingly. For the first equation, the slope is 2, and the y-intercept is -3. Points are plotted using the 'rise over run' method, resulting in a line that intersects the y-axis at -3 and other points such as (1, -1), (2, 1), and (3, 3). The second equation has a y-intercept of 5 and a slope of -2/3, leading to a different set of plotted points. The intersection point, (3, 3), is identified as the solution to the system.

05:01
🔍 Verifying the Solution by Substitution

The second paragraph demonstrates the verification of the solution obtained through graphing by using the substitution method. The instructor substitutes the expression for y from the first equation (2x - 3) into the second equation, resulting in an equation without y. The goal is to solve for x. To eliminate the fraction, the equation is multiplied by 3, leading to a linear equation in terms of x. The instructor simplifies the equation step by step, combining like terms and solving for x, which results in x = 3. This value is then substituted back into the equation to find the corresponding y value, which is also 3. The solution (3, 3) is confirmed to be correct, matching the point of intersection found through graphing. This step ensures the accuracy of the graphical solution and reinforces the understanding of solving systems of equations.

Mindmap
Keywords
💡System of Equations
A system of equations refers to a collection of multiple equations that need to be solved simultaneously. In the context of this video, the system consists of two linear equations. The main theme revolves around finding the point of intersection of these equations, which represents the solution to the system. The script describes the process of solving a system of equations by graphing, which involves plotting both equations on the same graph and identifying where their lines intersect.
💡Graphing
Graphing is a method used to visually represent mathematical equations on a coordinate plane. It is central to the video's narrative as the instructor demonstrates how to graph two equations to find their point of intersection. The script explains the importance of drawing a large graph to clearly see the solution and provides step-by-step instructions on how to plot points based on the equations' slopes and intercepts.
💡Slope-Intercept Form
The slope-intercept form of a linear equation is written as y = mx + b, where 'm' is the slope and 'b' is the y-intercept. This form is crucial in the video because it allows for easy identification of the slope and y-intercept, which are then used to plot the line on the graph. The script mentions that both equations are in slope-intercept form, making it straightforward to graph the first equation with a slope of 2 and a y-intercept of -3.
💡Slope
Slope is a measure of the steepness of a line, indicating how much the y-value changes with respect to the x-value. In the video, the slope is used to determine the direction and steepness of the lines when graphing the equations. The first equation has a slope of 2, meaning for every one unit increase in x, y increases by two units, while the second equation has a slope of -2/3, indicating a downward slope.
💡Y-Intercept
The y-intercept is the point where a line crosses the y-axis on a graph. It is represented as 'b' in the slope-intercept form of a line. In the video, the y-intercepts are used as starting points for graphing the lines. The first equation has a y-intercept of -3, and the second equation has a y-intercept of 5, which are the initial points from which the lines are drawn.
💡Point of Intersection
The point of intersection is the coordinate where two lines on a graph meet. It is the solution to the system of equations being graphed. The video's main goal is to find this point by plotting both equations and determining where they intersect. The script describes the process of graphing and concludes that the point of intersection is (3, 3).
💡Substitution
Substitution is a method used to solve systems of equations algebraically by expressing one variable in terms of another and then substituting it into the other equation. In the video, after graphing, the instructor uses substitution to verify the graphical solution. The script shows the algebraic process of substituting y with 2x - 3 into the second equation and solving for x.
💡Rise Over Run
Rise over run is a phrase used to describe the slope of a line in the context of graphing. It refers to the vertical change (rise) and the horizontal change (run) between two points on the line. The script uses this concept to explain how to find additional points on the graph by moving up by the rise and over by the run, based on the slope of the line.
💡Fraction
A fraction represents a part of a whole, expressed as a ratio of two integers. In the video, the term is used in the context of the second equation's slope, which is -2/3. The script explains how to eliminate the fraction by multiplying through by the denominator to simplify the equation, which is a common algebraic technique.
💡Algebraic Solution
An algebraic solution is a method of finding the values of variables in an equation or system of equations using algebraic manipulation. The video demonstrates both graphical and algebraic methods to solve the system. After graphing, the instructor provides an algebraic solution by multiplying through by 3 to clear the fraction and solving for x, which confirms the graphical solution of x = 3 and y = 3.
Highlights

Lesson focuses on solving a system of equations by graphing.

First equation is y = 2x - 3.

Second equation is -2/3x + 5.

Objective is to graph both equations and find the point of intersection.

Advantage of a large graph for clarity in finding the solution.

Equations are in slope-intercept form.

First equation has a slope (m) of 2 and y-intercept of -3.

Demonstration of finding points for the first equation using slope.

Second equation has a y-intercept of 5 and slope of -2/3.

Graphing the second equation with points derived from its slope.

Point of intersection identified as (3, 3).

Verification of the solution by substitution method.

Elimination of fractions by multiplying through by 3.

Solving for x gives the value of 3.

Substituting x back into an equation to solve for y.

Final solution confirmed as (3, 3), matching the graphed intersection.

Transcripts

Browse More Related Video

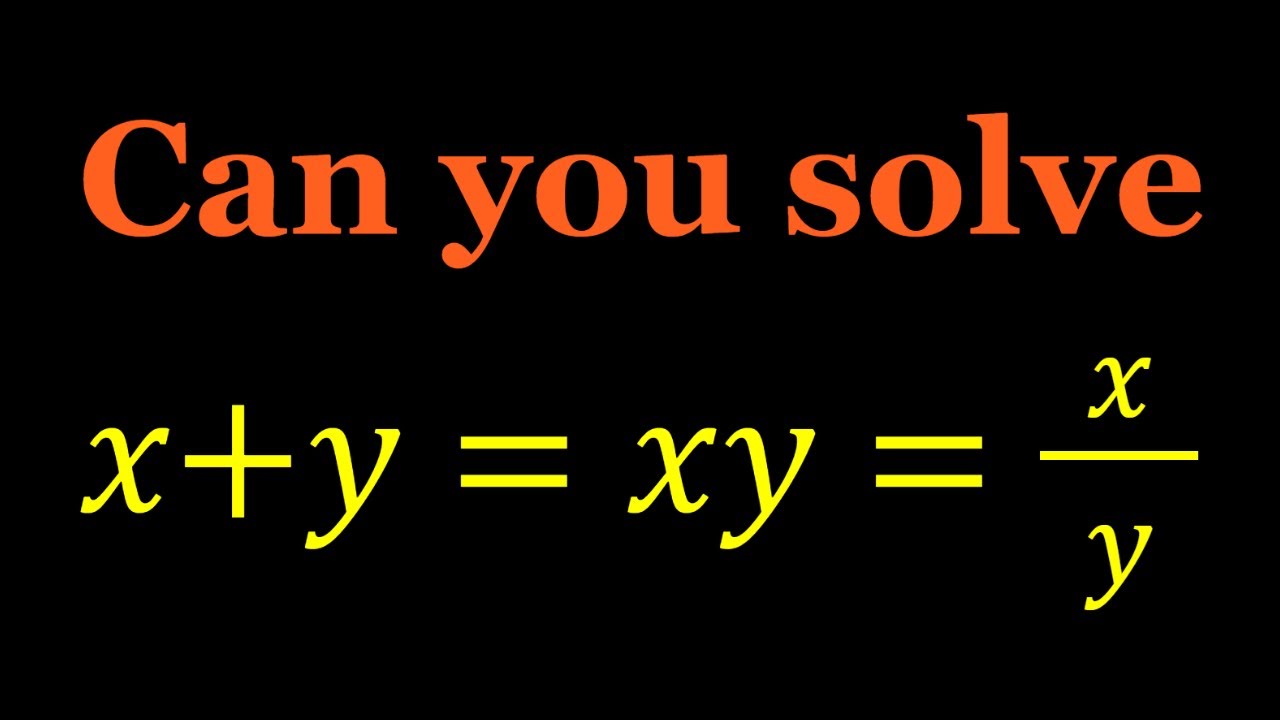
Solving a System Equations | #Algebra

4 Steps to Graphing Slope-Intercept Form | 8.EE.B.6 💗

SOLVING SYSYEM OF NONLINEAR EQUATIONS || PRECALCULUS

Solving Exponential Equations Using Logarithms & The Quadratic Formula

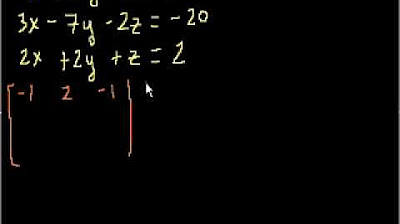
Solving 3 Equations with 3 Unknowns

Ex: Solve a Polynomial Equation Using a Graphing Calculator (Approximate Solutions)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AlgebraGraphingSolving EquationsEducationalMath TutorialSlope-InterceptSubstitution MethodMathematicsLearning ResourceProblem Solving