Angular Momentum and Cross Product | Physics with Professor Matt Anderson | M12-15
TLDRIn this educational transcript, Professor Anderson delves into the concept of angular momentum, a fundamental principle in physics related to rotational motion. He begins by contrasting angular momentum (denoted as 'L') with linear momentum ('p'), which is simply the product of mass and velocity (m*v). Angular momentum is described by the cross product of the radius vector (r), representing the distance from the axis of rotation to the object, and the linear momentum (p) of the object. The cross product, symbolized by the 'x', results in a vector quantity, distinct from the scalar outcome of the dot product. Professor Anderson emphasizes the importance of understanding the cross product, which is calculated as the product of the magnitudes of the two vectors and the sine of the angle (phi) between them. To determine the direction of the cross product, he introduces the right-hand rule, a technique that uses the right hand to visualize the direction of the resulting vector. The professor illustrates this with an example involving two vectors at a right angle, demonstrating how the right-hand rule leads to the determination of the direction of the cross product. The summary concludes with an encouragement for students to practice the right-hand rule at home to solidify their understanding of angular momentum.
Takeaways
- 📚 Angular momentum is related to rotational motion and is distinct from linear momentum.
- 📐 The formula for angular momentum (L) is L = r × p, where r is the distance from the axis of rotation to the object, and p is the linear momentum of the object.
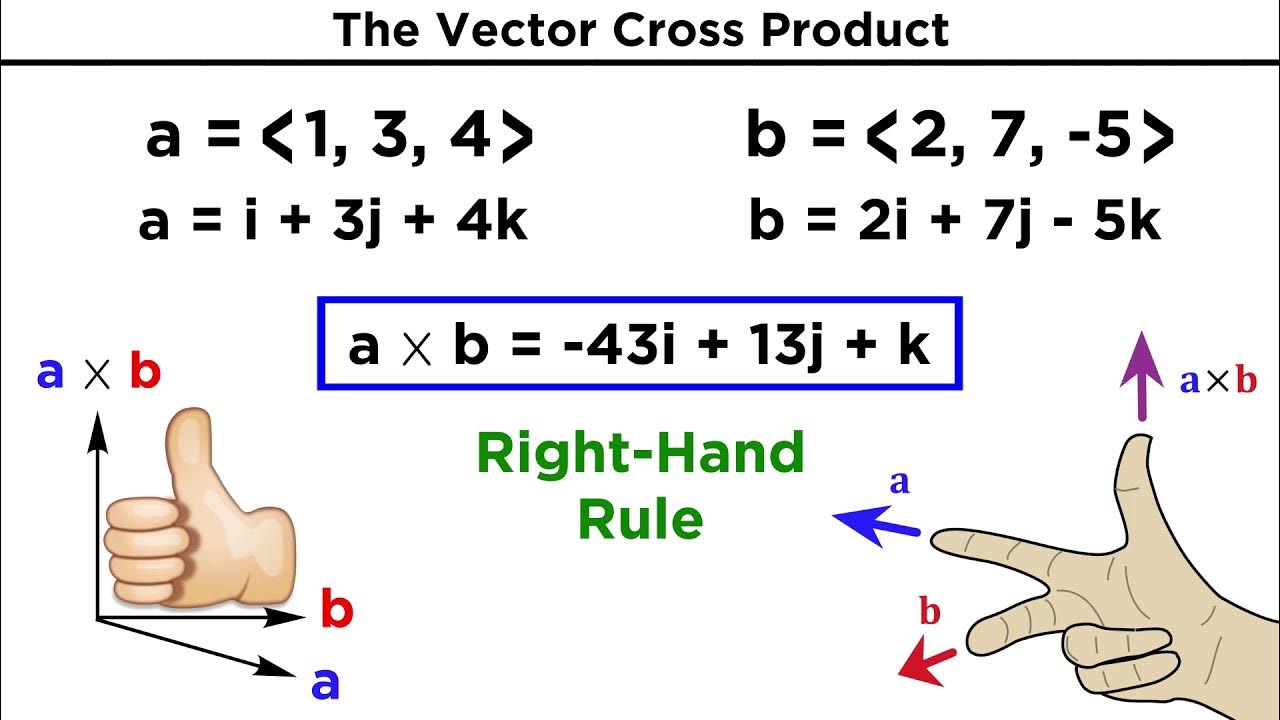
- ✖️ The cross product (×) is a mathematical operation that combines two vectors to produce a third vector, unlike the dot product which results in a scalar.
- 📏 The magnitude of the cross product between two vectors a and b is given by |a| * |b| * sin(φ), where φ is the angle between the vectors.
- 🧭 The direction of the cross product is determined by the right-hand rule, which is a method to find the direction of the resultant vector.
- ✋ The right-hand rule states that if you point the fingers of your right hand in the direction of vector a, and then curl them towards vector b, your thumb will point in the direction of the cross product.
- 🕹️ When vectors a and b are perpendicular (90 degrees), the magnitude of the cross product simplifies to |a| * |b| because sin(90°) is 1.
- 🖐 The direction of the cross product is perpendicular to the plane formed by the original vectors a and b.
- 🔄 Angular momentum is a vector quantity, which is why it is represented with a vector symbol (L) on top of the equation.
- 🤔 Understanding the cross product is crucial for solving problems involving angular momentum.
- 📈 The cross product is a fundamental concept in physics, particularly in the study of three-dimensional motion and forces.
Q & A
What is the primary topic of discussion in the provided transcript?
-The primary topic of discussion is angular momentum and its relationship to linear momentum and rotational motion.
How is angular momentum mathematically represented?
-Angular momentum is represented by the symbol 'L' and is mathematically expressed as L = r × p, where 'r' is the distance from the axis of rotation to the object, and 'p' is the linear momentum of the object.
What is the cross product in the context of angular momentum?
-The cross product is a mathematical operation that combines two vectors to yield another vector. In the context of angular momentum, it is used to calculate the vector product of the position vector 'r' and the linear momentum vector 'p'.
Why is the cross product important in calculating angular momentum?
-The cross product is important because it maintains the vector quantity of angular momentum, which is essential for describing the rotational motion of an object.
What is the magnitude of the cross product between two vectors?
-The magnitude of the cross product between two vectors A and B is given by |A| * |B| * sin(φ), where |A| and |B| are the magnitudes of vectors A and B, respectively, and φ is the angle between them.
How is the direction of the cross product determined?
-The direction of the cross product is determined using the right-hand rule, which states that if you point the fingers of your right hand in the direction of vector A and then curl them towards vector B, your thumb will point in the direction of the cross product.
What is the right-hand rule, and how does it apply to the cross product?
-The right-hand rule is a mnemonic tool used to determine the direction of the cross product. It states that if you align your right hand such that your fingers point in the direction of the first vector, and then curl your fingers towards the second vector, your thumb will point in the direction of the resulting cross product.
What is the significance of the sine function in the magnitude of the cross product?
-The sine function in the magnitude of the cross product accounts for the angle between the two vectors being multiplied. It ensures that the cross product is non-zero only when the vectors are not parallel, which is consistent with the geometric interpretation of the cross product as an area vector.
How does the angle between two vectors affect the magnitude of their cross product?
-The angle between two vectors directly affects the magnitude of their cross product through the sine of the angle. When the angle is 90 degrees (perpendicular), the sine function reaches its maximum value of 1, resulting in the maximum magnitude for the cross product.
What happens if the two vectors are parallel or antiparallel?
-If the two vectors are parallel or antiparallel, the angle between them is either 0 or 180 degrees. In both cases, the sine of the angle is 0, which means the magnitude of their cross product is also 0.
Can you provide an example of how to apply the right-hand rule to find the direction of the cross product?
-Certainly. If vector A is pointing to the right and vector B is pointing upwards, you would point your fingers straight in the direction of A (to the right), then curl them towards B (upwards). Your thumb will then point outwards, away from the screen, which is the direction of the cross product C in this case.
What is the role of linear momentum in the calculation of angular momentum?
-Linear momentum, represented by 'p', is a vector quantity that, when combined with the position vector 'r' through the cross product, gives the angular momentum 'L'. It is the momentum of an object in linear motion that contributes to the rotational motion when considering angular momentum.
Outlines
📚 Understanding Angular Momentum and Cross Product
Professor Anderson introduces the concept of angular momentum in relation to rotational motion. He explains that angular momentum (denoted as L) is the rotational analog to linear momentum (P), and is given by the cross product of the radius vector (r) and the linear momentum (p). The radius vector represents the distance from the axis of rotation to the object, while the cross product is a mathematical operation that combines two vectors to yield another vector. The professor emphasizes the importance of the right-hand rule for determining the direction of the resultant vector from the cross product, which is crucial for solving angular momentum problems.
🤔 Applying the Right-Hand Rule to Cross Product
The second paragraph delves into the specifics of the right-hand rule, which is used to determine the direction of the cross product between two vectors. The professor uses a simple example with vector a pointing to the right and vector b pointing upwards to illustrate how the right-hand rule works. He explains that when the fingers of the right hand are pointed in the direction of vector a and then curled towards vector b, the thumb points in the direction of the cross product (vector c). This demonstration clarifies that for vectors a and b at a right angle, the magnitude of the cross product is simply the product of the magnitudes of a and b, and the direction is perpendicular to the plane formed by a and b, following the right-hand rule.
Mindmap
Keywords
💡Angular Momentum
💡Linear Momentum
💡Cross Product
💡Right-Hand Rule
💡Vector
💡Dot Product
💡Radius Vector
💡Rotational Motion
💡Sine of the Angle
💡Scalar Quantity
💡Vector Magnitude
Highlights
Angular momentum is related to rotational motion and is different from linear momentum.
Angular momentum (L) is represented as the cross product of the radius vector (r) and the linear momentum (p), written as L = r × p.
The radius vector (r) is the distance from the axis of rotation to the object.
Linear momentum (p) is the product of an object's mass (m) and its velocity (v).
The cross product results in a vector quantity, unlike the dot product which results in a scalar.
The magnitude of the cross product between two vectors a and b is given by |a| * |b| * sin(φ), where φ is the angle between the vectors.
The direction of the cross product is determined by the right-hand rule.
The right-hand rule states that if you point the fingers of your right hand in the direction of vector a, curl them towards vector b, your thumb will point in the direction of the cross product.
When vectors a and b are perpendicular, the sine of the angle between them is 1, simplifying the cross product magnitude to simply |a| * |b|.
For the example given, with vector a pointing to the right and vector b pointing up, the cross product direction is out of the screen.
The cross product is a fundamental concept for understanding angular momentum in physics.
Understanding the cross product is essential for solving various angular momentum problems.
The professor emphasizes the importance of mastering the right-hand rule for determining the direction of the cross product.
The lecture provides a practical demonstration of the right-hand rule using the example of vectors a and b.
Students are encouraged to practice the right-hand rule at home to solidify their understanding of the cross product.
The lecture concludes with an invitation for students to seek additional help during office hours if they struggle with the right-hand rule.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: