How to Calculate the Vector Cross Product
TLDRThis engineering mechanics lesson dives deep into the concept of the cross product, a fundamental operation in vector mathematics with broad applications across physics, engineering, and beyond. The instructor begins by contrasting the cross product with the dot product, emphasizing that the cross product results in a vector, not a scalar, and depends on the sine of the angle between two vectors. The lesson then explores the magnitude and direction of the cross product, introducing the right-hand rule to determine direction. The importance of the 90-degree angle for maximum cross product magnitude is highlighted, tying into the concept of moments in mechanics. The distinction between the directions of cross products ( \u0027mathbf{A} \u0027times \u0027mathbf{B}\u0027 ) and ( \u0027mathbf{B} \u0027times \u0027mathbf{A}\u0027 ) is clarified, noting that order matters due to the directional nature of the cross product. The instructor presents a methodical approach to calculating the cross product, starting with the manual expansion of component-wise multiplication and leading up to the elegant use of determinants for a more streamlined calculation. The script concludes with practical examples that reinforce the cross product's utility in calculating moments in three-dimensional space, preparing learners for more complex applications in their studies.
Takeaways
- 📚 The cross product of two vectors results in a third vector, which has both magnitude and direction, unlike the dot product which results in a scalar.
- ✋ The magnitude of the cross product is given by the formula |A| * |B| * sin(θ), where |A| and |B| are the magnitudes of the vectors and θ is the angle between them.
- ➡️ The direction of the cross product follows the right-hand rule, which determines the direction of the resulting vector based on the orientation of the initial vectors.
- 🚫 The cross product is non-commutative, meaning A cross B does not equal B cross A, due to the directional nature of the cross product.
- 📈 The cross product reaches its maximum magnitude when the angle between the two vectors is 90 degrees, resulting in a vector perpendicular to the plane formed by the two vectors.
- 📉 If the angle between the two vectors is 0 or 180 degrees, the cross product is zero, as the vectors are collinear.
- 🧮 Calculating the cross product of unit vectors (i, j, k) can be done using a simple table or by visualizing the vectors and applying the right-hand rule.
- 🎯 The cross product is a fundamental concept in various fields such as physics, engineering, and mathematics, and is used to calculate moments and forces in three dimensions.
- 📏 A practical method for calculating the cross product is by using the determinant of a matrix, which simplifies the process and reduces the likelihood of errors.
- 📐 The matrix method involves writing the unit vectors (i, j, k) as the first row, the components of vector A as the second row, and the components of vector B as the third row, then calculating the determinant.
- 🔍 The determinant method is efficient and visual, allowing for quick calculation of the cross product without memorizing complex formulas.
Q & A
What is the cross product of two vectors?
-The cross product of two vectors is a vector that results from the vector multiplication of two vectors in three-dimensional space. It is denoted by the symbol '×' and has both a magnitude and a direction, unlike the dot product which results in a scalar.
How is the magnitude of the cross product of two vectors calculated?
-The magnitude of the cross product, |C|, is calculated as the product of the magnitudes of the two vectors, |A| and |B|, and the sine of the angle between them, θ, i.e., |C| = |A| * |B| * sin(θ).
What is the role of the right-hand rule in determining the direction of the cross product?
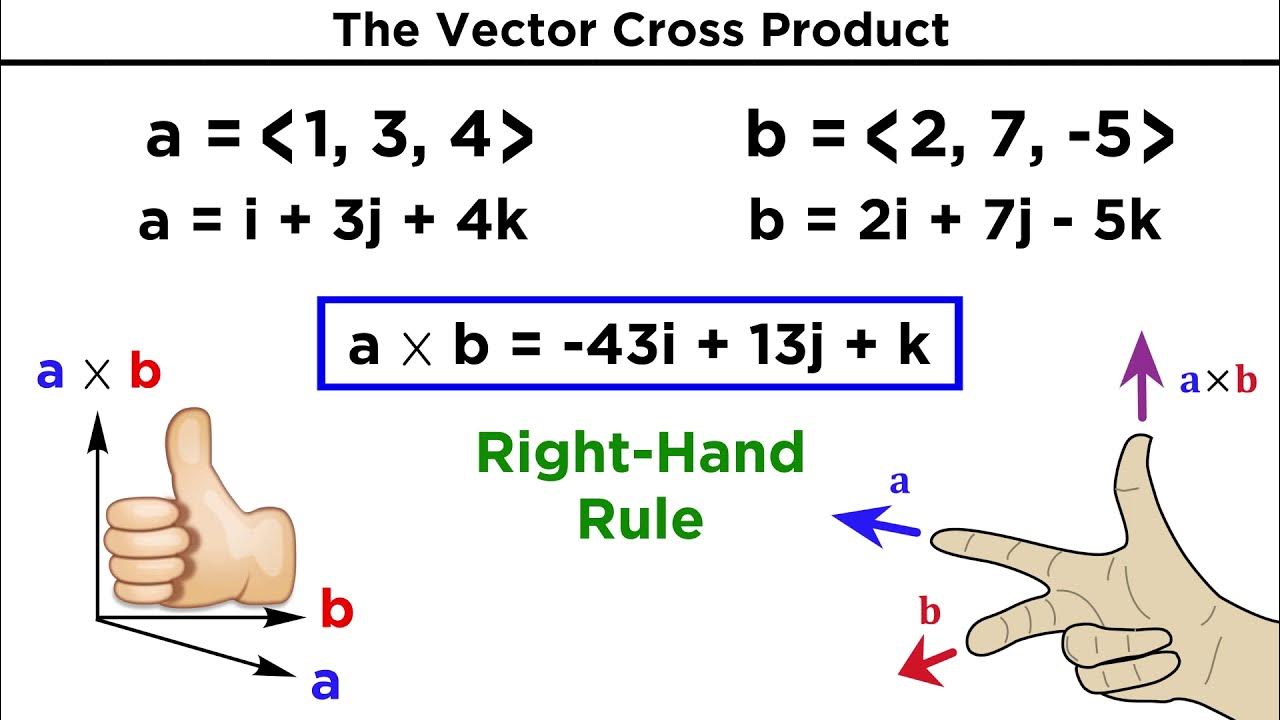
-The right-hand rule is used to determine the direction of the cross product. If you point your right hand such that your fingers point in the direction of the first vector and then curl them towards the second vector, your thumb will point in the direction of the resulting cross product.
What happens to the cross product when the angle between two vectors is 90 degrees?
-When the angle between two vectors is 90 degrees, the sine of the angle is 1, which means the cross product is at its maximum magnitude, which is the product of the magnitudes of the two vectors.
What is the relationship between the cross product and the dot product in terms of their magnitudes?
-The magnitude of the cross product of two vectors is similar to the dot product in that both involve the magnitudes of the vectors and the angle between them. However, the cross product uses the sine of the angle, while the dot product uses the cosine of the angle.
Why is it important to consider the order of the vectors when calculating the cross product?
-The order of the vectors is important because the cross product is not commutative. This means that the cross product of vector A with vector B is not the same as the cross product of vector B with vector A; the direction of the resulting vector will be different.
How can you calculate the cross product of two unit vectors?
-The cross product of two unit vectors, which are perpendicular to each other, can be calculated using the right-hand rule. For example, the cross product of unit vector I with unit vector J results in unit vector K, which is perpendicular to both I and J.
What is the determinant method for calculating the cross product?
-The determinant method involves writing the cross product as the determinant of a 3x3 matrix. The first row of the matrix consists of the unit vectors i, j, and k, the second row consists of the components of vector A, and the third row consists of the components of vector B. The determinant of this matrix gives the result of the cross product.
What is the significance of the determinant method in calculating the cross product?
-The determinant method simplifies the process of calculating the cross product by reducing the need to remember complex formulas. It provides a systematic way to find the components of the resulting vector by calculating the determinant of specific sub-matrices.
How does the determinant method help in remembering the cross product calculation?
-The determinant method provides a visual representation of the cross product calculation. By focusing on one component at a time and using the criss-cross multiplication pattern, it becomes easier to remember and apply the calculation without having to memorize the entire formula.
What is the practical application of the cross product in engineering and physics?
-The cross product is widely used in engineering and physics for various applications such as calculating moments in mechanics, determining areas and volumes, and in the study of electricity and magnetism. It is a fundamental operation in vector algebra and has practical implications in numerous fields.
Outlines
📚 Introduction to Cross Product in Engineering Mechanics
The first paragraph introduces the topic of the cross product in the context of engineering mechanics. It emphasizes the mathematical definition and distinguishes the cross product from the dot product. The speaker previews the application of cross products in three dimensions, noting the increased complexity compared to two-dimensional calculations. The lesson aims to build confidence in understanding and calculating vector cross products, with a promise that the effort will be rewarded with a deeper comprehension by the end of the lesson.
🔍 Exploring the Magnitude and Direction of Cross Products
This paragraph delves into the specifics of the cross product's magnitude and direction. It contrasts the cross product with the dot product, highlighting that the cross product results in a vector, not a scalar. The magnitude of the cross product is detailed as the product of the magnitudes of the two vectors and the sine of the angle between them. The direction is determined by the right-hand rule, which is a concept that will be revisited when discussing moments, which are essentially cross products of force and moment arms.
🤔 Understanding the Cross Product with Unit Vectors
The third paragraph focuses on the concept of crossing unit vectors to better understand the cross product. It explains that unit vectors, despite their simplicity, can be crossed just like any other vector. The paragraph outlines the results of crossing the unit vectors i, j, and k with one another, using the right-hand rule to determine the direction of the resulting vectors. This section provides a foundation for visualizing the cross product in three-dimensional space.
📝 Calculating the Cross Product of Arbitrary Vectors
The fourth paragraph demonstrates how to calculate the cross product of non-unit vectors. It presents a detailed, step-by-step process that involves expanding the cross product into its components and then simplifying. The paragraph also contrasts this method with a more straightforward approach using determinants, which is introduced as a more efficient way to calculate the cross product, especially for larger vectors.
🧮 Cross Product Formula and Its Components
This paragraph presents the general formula for the cross product, which can appear daunting due to its complexity. The formula is broken down into its components, relating to the x, y, and z components of the vectors being multiplied. The explanation shows how each component of the cross product is calculated, providing a clear connection to the earlier discussion on the magnitude and direction of the cross product.
🎓 Mastering Cross Products with Determinants
The sixth paragraph introduces an alternative method for calculating the cross product using determinants. This approach simplifies the process by utilizing a 3x3 matrix filled with unit vectors and the components of the vectors being multiplied. The determinant of this matrix yields the cross product, making it easier to remember and apply. The paragraph demonstrates how this method streamlines the calculation and emphasizes its utility in various engineering and physics contexts.
📐 Practical Application of Cross Product Determinants
The seventh paragraph reinforces the practical use of cross product determinants with an example. It walks through the process of setting up the matrix and calculating the determinant for two given vectors. The explanation underscores the ease of use and the visual nature of the determinant method, which helps in avoiding common errors associated with the traditional cross product formula.
🌟 The Significance of Cross Product Determinants in Education
In the final paragraph, the speaker reiterates the importance of mastering the cross product determinant method. It is highlighted as a valuable skill for future studies and applications in various fields. The paragraph summarizes the evolution of the cross product calculation methods covered in the lesson, from the basic understanding to the more complex formula, and finally to the determinant method, which is positioned as the preferred approach for its clarity and efficiency.
Mindmap
Keywords
💡Cross Product
💡Dot Product
💡Magnitude
💡Direction
💡Right-Hand Rule
💡Unit Vectors
💡Determinant
💡Vector Components
💡Sine and Cosine
💡Perpendicular
💡Engineering Mechanics
Highlights
The cross product of two vectors is a vector that has both magnitude and direction, differing from the dot product which results in a scalar.
The magnitude of the cross product is given by the formula |A|*|B|*sin(θ), where |A| and |B| are the magnitudes of vectors A and B, and θ is the angle between them.
The direction of the cross product is determined by the right-hand rule, which states that if you point the fingers of your right hand in the direction of the first vector and curl them towards the second vector, your thumb will point in the direction of the cross product.
The cross product is maximized when the angle between the two vectors is 90 degrees, resulting in a vector perpendicular to the plane containing the original vectors.
When the angle between the two vectors is 0 or 180 degrees, the cross product is zero, indicating that the vectors are collinear.
The cross product is anti-commutative, meaning that A cross B is not equal to B cross A, due to the directionality of the resulting vector.
Crossing unit vectors (i, j, k) is a key method to understand the cross product, as they are perpendicular to each other and have a magnitude of one.
A mnemonic table or chart can be used to remember the results of crossing unit vectors, which helps in visualizing the direction of the cross product.
The cross product of two non-unit vectors A and B involves multiplying each component of one vector by each component of the other vector and then applying the cross product rules.
There's a standard formula for the cross product in terms of the components of vectors A and B, which can be complex but is systematic.
The cross product has practical applications in various fields such as mechanics, electricity, magnetism, thermodynamics, and physics.
A more intuitive and less cumbersome method for calculating the cross product is using the determinant of a matrix, which simplifies the process.
The determinant method involves placing the unit vectors i, j, k at the top of a matrix, the components of vector A in the middle, and the components of vector B at the bottom.
Calculating the determinant of the matrix for the cross product involves a crisscross pattern of multiplication and subtraction, yielding the i, j, and k components of the resulting vector.
The determinant method is a visual representation of the cross product calculation, making it easier to remember and apply.
The determinant method is particularly useful for quick calculations and for those who need to calculate cross products frequently in their work or studies.
The lesson emphasizes the importance of understanding the cross product for students of engineering and physics, and provides a solid foundation for future studies.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: