Angular momentum and cross product
TLDRIn this engaging lecture, Anderson introduces the concept of angular momentum, a fundamental principle in physics that pertains to rotational motion. He begins by contrasting angular momentum (denoted as L) with linear momentum (P), which is simply the product of mass (M) and velocity (V). Anderson then explains that angular momentum is given by the cross product of the radius vector (R), which represents the distance from the axis of rotation to the object, and the linear momentum (P) of the object. The cross product, symbolized by the 'X', is a mathematical operation that combines two vectors to yield another vector, as opposed to the dot product, which results in a scalar. Anderson delves into the specifics of the cross product, illustrating how it is calculated using the magnitudes of the two vectors and the sine of the angle between them. He emphasizes the importance of the right-hand rule for determining the direction of the cross product, which is crucial for understanding angular momentum. Anderson provides a practical example using vectors pointing in the right and up directions to demonstrate the calculation and direction of the cross product. The lecture is concluded with an invitation for students to practice the right-hand rule and seek clarification during office hours if needed.
Takeaways
- 📐 Angular momentum (L) is related to rotational motion and is different from linear momentum (P).
- 🔵 Angular momentum is represented by the symbol L and is calculated as the cross product of the radius vector (R) and the linear momentum (P), written as L = R × P.
- 📏 The radius vector (R) is the distance from the axis of rotation to the object.
- 🚀 The linear momentum (P) is the product of the object's mass (M) and its velocity (V), expressed as P = M × V.
- ✖️ The cross product is a mathematical operation that combines two vectors to produce a third vector, distinct from the dot product which yields a scalar.
- 📏 The magnitude of the cross product between two vectors A and B is given by |A| × |B| × sin(θ), where θ is the angle between the vectors.
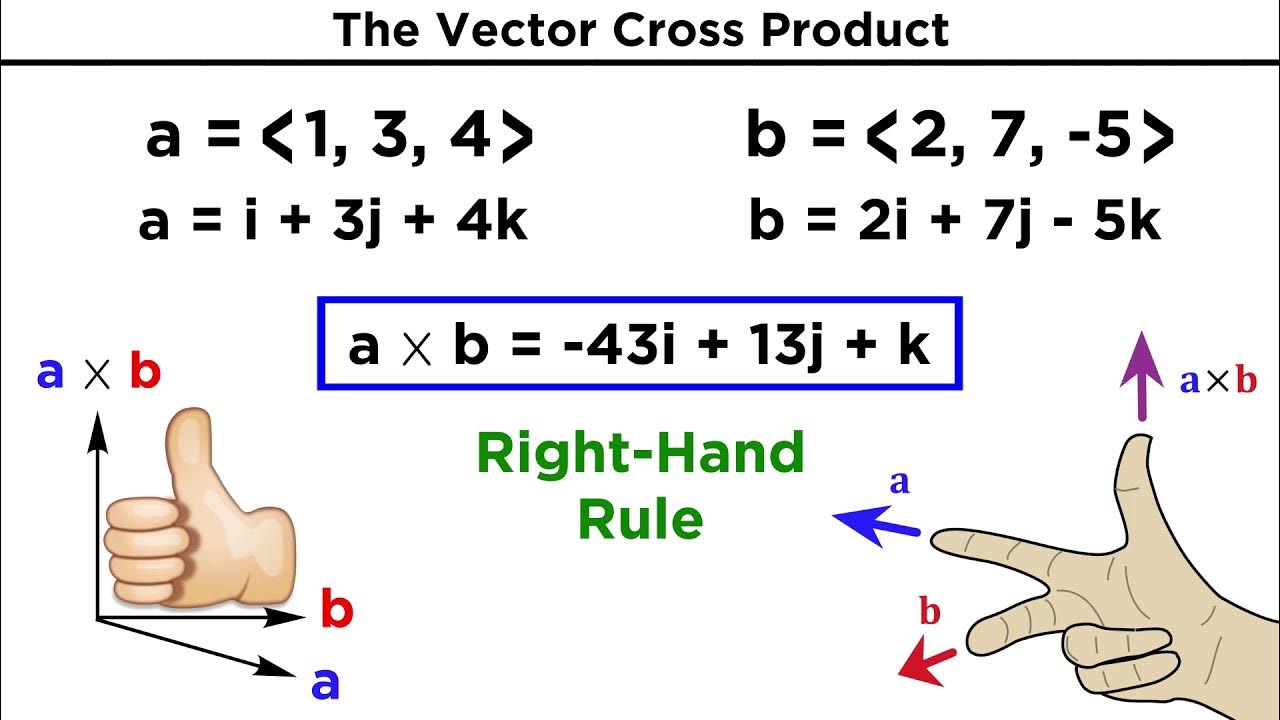
- 🧭 The direction of the cross product is determined by the right-hand rule, which dictates that the direction is perpendicular to both original vectors.
- ✋ The right-hand rule is applied by pointing the fingers of the right hand in the direction of vector A, then curling them towards vector B, with the thumb pointing in the direction of the resulting vector C.
- 🤚 A common demonstration of the right-hand rule involves pointing the fingers straight in the direction of vector A (right), then curling them towards vector B (up), resulting in the thumb pointing out of the screen (direction of vector C).
- 🔁 The cross product is anticommutative, meaning that A × B is equal to - (B × A), which is a key property when considering the direction of the resulting vector.
- 📚 Understanding the cross product is crucial for solving problems involving angular momentum, as it helps to determine the direction of the rotational motion vector.
Q & A
What is angular momentum?
-Angular momentum, denoted by L, is a measure of an object's rotational motion. It is the product of the radius vector (R), which is the distance from the axis of rotation to the object, and the linear momentum (P) of the object, represented by the cross product R cross P.
What is the cross product and how does it relate to angular momentum?
-The cross product is a mathematical operation that combines two vectors to produce a third vector. It is used to calculate angular momentum because it maintains a vector quantity. The cross product of the radius vector (R) and the linear momentum (P) gives the angular momentum (L).
How is the magnitude of the cross product calculated?
-The magnitude of the cross product between two vectors A and B is calculated as the product of the magnitudes of A and B, and the sine of the angle (V) between them, which is given by |A cross B| = |A| * |B| * sin(V).
What is the right-hand rule and how is it used to determine the direction of the cross product?
-The right-hand rule is a mnemonic used to determine the direction of the cross product. To apply it, one points the fingers of the right hand in the direction of vector A and then curls them towards vector B. The direction that the thumb points is the direction of the cross product vector C.
Why is the sine function used in the calculation of the cross product?
-The sine function is used in the calculation of the cross product because it relates the magnitudes of the two vectors and the angle between them. It ensures that the resulting cross product is a vector that is perpendicular to both original vectors.
What is the difference between the dot product and the cross product of two vectors?
-The dot product of two vectors results in a scalar quantity, which is the product of the magnitudes of the vectors and the cosine of the angle between them. In contrast, the cross product results in a vector quantity that is perpendicular to both original vectors and is calculated using the sine of the angle between them.
What happens if the angle between two vectors is a right angle in the calculation of the cross product?
-If the angle between two vectors is a right angle (90 degrees), the sine of the angle is 1. Therefore, the magnitude of the cross product is equal to the product of the magnitudes of the two vectors, as sin(90 degrees) = 1.
How can one visualize the direction of the cross product using the right-hand rule?
-To visualize the direction of the cross product, one can extend the index finger in the direction of vector A and then curl it towards vector B. The direction that the thumb points represents the direction of the cross product vector C.
What is the physical significance of angular momentum?
-The physical significance of angular momentum is that it is a measure of how much an object is rotating. It is a conserved quantity, meaning it remains constant if no external torques are applied to the system.
Can angular momentum be negative?
-Angular momentum can be negative, which indicates the direction of rotation. If the rotation is counterclockwise when viewed from the end of the radius vector (R), the angular momentum is considered positive. If it is clockwise, it is negative.
How does the linear momentum of an object contribute to its angular momentum?
-The linear momentum of an object contributes to its angular momentum through the cross product with the radius vector. The greater the linear momentum or the further the object is from the axis of rotation, the larger the angular momentum will be.
What is the role of the axis of rotation in angular momentum?
-The axis of rotation is the reference point about which the object is rotating. The radius vector (R) extends from the axis of rotation to the object, and its length and orientation with respect to the linear momentum vector (P) determine the magnitude and direction of the angular momentum.
Outlines
📚 Introduction to Angular Momentum
In this paragraph, Anderson introduces the concept of angular momentum, which is related to rotational motion. He contrasts it with linear momentum, denoted as P, which is the product of mass (M) and velocity (V). Angular momentum is symbolized by L and is defined as the cross product of the radius vector (R), which represents the distance from the axis of rotation to the object, and the linear momentum (P). Anderson explains the cross product as a mathematical operation that combines two vectors while maintaining a vector quantity, as opposed to the dot product, which results in a scalar. The cross product is further characterized by its magnitude, which is the product of the magnitudes of the two vectors and the sine of the angle between them, and its direction, which is determined by the right-hand rule.
🤔 Understanding the Cross Product and the Right-Hand Rule
This paragraph delves into the specifics of the cross product and the right-hand rule. Anderson explains that the cross product between two vectors, A and B, is a vector quantity that requires both magnitude and direction. The magnitude is calculated as the product of the magnitudes of the two vectors and the sine of the angle between them. To determine the direction of the cross product, Anderson describes using the right-hand rule. He demonstrates this with an example where vector A points to the right and vector B points up, resulting in a cross product that is perpendicular to both A and B and comes out of the screen, as determined by the right-hand rule. Anderson encourages students to practice this at home and offers help during office hours for those who find it challenging.
Mindmap
Keywords
💡Angular Momentum
💡Linear Momentum
💡Cross Product
💡Vector
💡Right-Hand Rule
💡Radius Vector
💡Dot Product
💡Scalar
💡Sine of the Angle
💡Direction
💡Office Hours
Highlights
Angular momentum is introduced as a concept related to rotational motion.
Angular momentum is denoted by the symbol L and is defined as the cross product of the radius vector and the linear momentum vector.
The radius vector (R) represents the distance from the axis of rotation to the object.
Linear momentum (P) is the product of mass (M) and velocity (V) of an object.
The cross product is a mathematical operation that combines two vectors to produce a third vector.
The cross product results in a vector quantity, as opposed to the dot product which results in a scalar.
The magnitude of the cross product is given by the product of the magnitudes of the two vectors and the sine of the angle between them.
The direction of the cross product is determined using the right-hand rule.
The right-hand rule involves extending the fingers of the right hand in the direction of the first vector, curling them towards the second vector, with the thumb pointing in the direction of the resulting vector.
When two vectors are perpendicular, the sine of the angle between them is 1, simplifying the cross product calculation.
An example is given where vector A points to the right and vector B points up, resulting in a cross product that points out of the screen.
The cross product is visualized by using the right hand to determine the direction of the resulting vector.
The lecturer suggests practicing the right-hand rule at home to better understand the direction of the cross product.
Office hours are offered for students who are having difficulty with the right-hand rule or the concept of angular momentum.
The lecture emphasizes the importance of understanding both the magnitude and direction of the cross product in the context of angular momentum.
The cross product is a fundamental tool for solving various angular momentum problems in physics.
The lecture concludes with an encouragement to apply the concepts learned to further explore angular momentum.
Transcripts
Browse More Related Video

Angular Momentum and Cross Product | Physics with Professor Matt Anderson | M12-15

What Is Angular Momentum?

Angular Momentum of a Spinning Wheel | Physics with Professor Matt Anderson | M12-16

Cross Product and Dot Product: Visual explanation
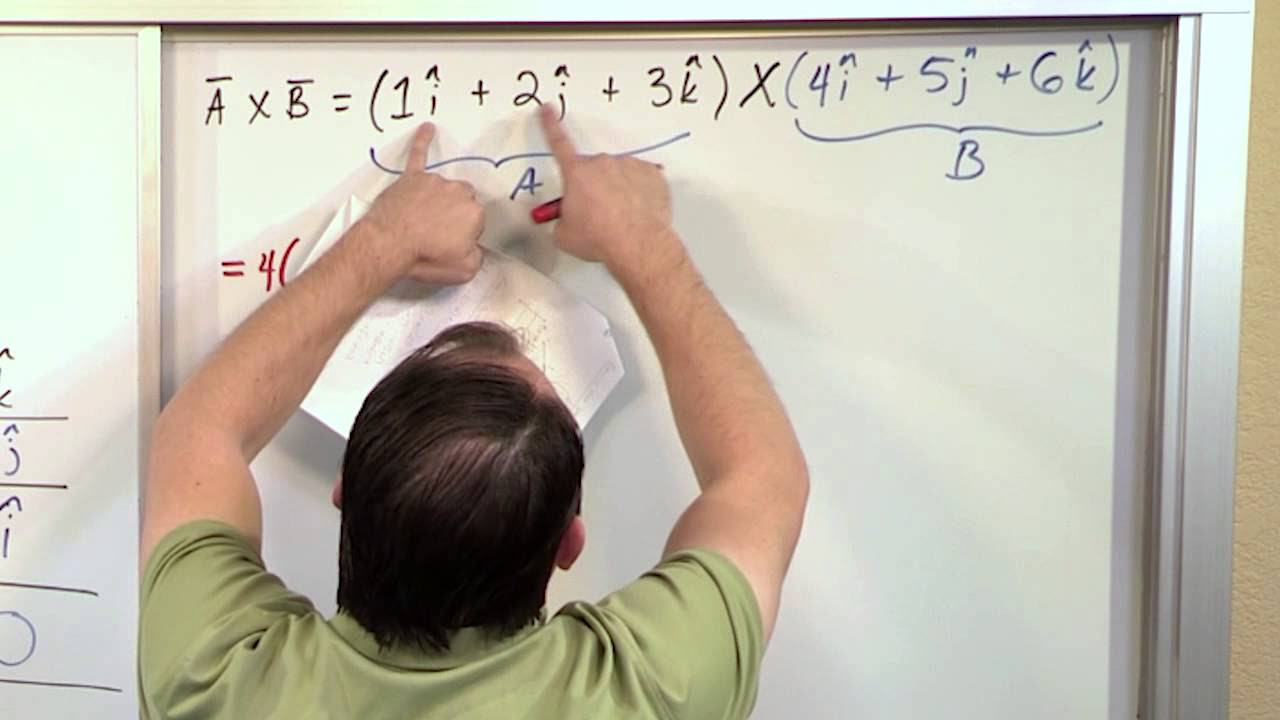
How to Calculate the Vector Cross Product
The Vector Cross Product
5.0 / 5 (0 votes)
Thanks for rating: