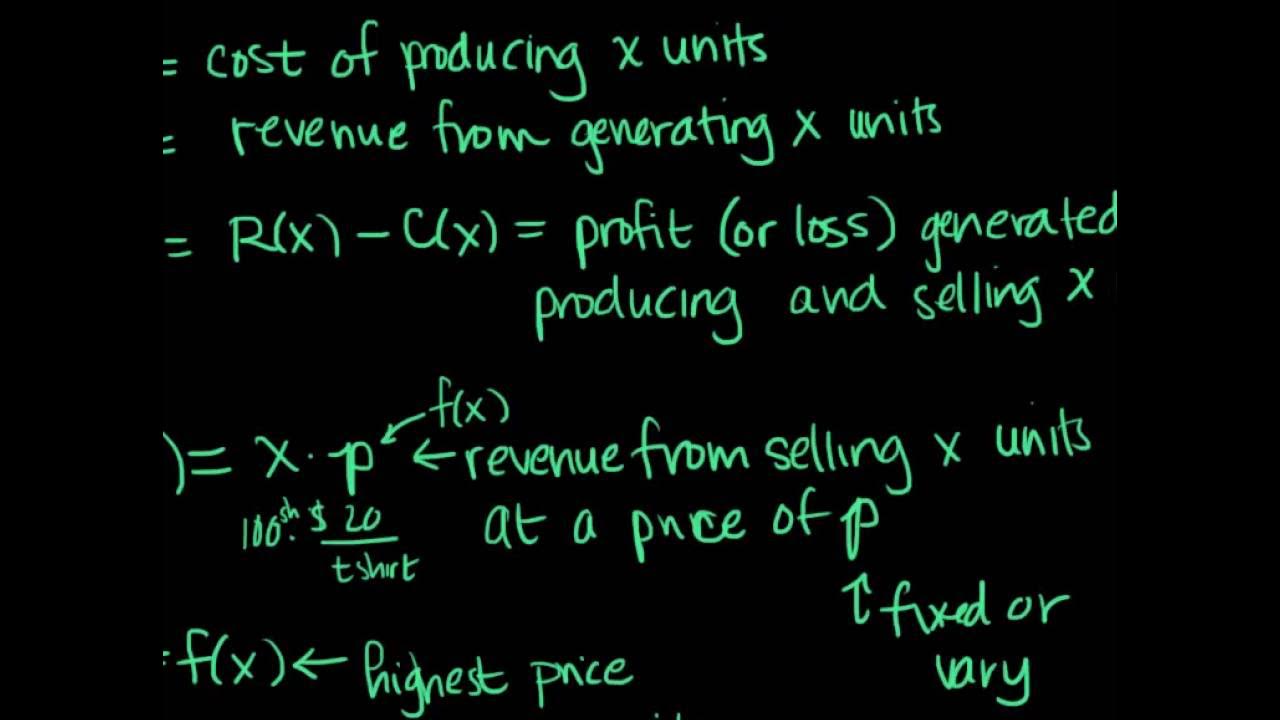Math1325 Lecture 10 3 - Optimization
TLDRThe video script is a comprehensive lecture on optimization in the context of business and economics, specifically tailored for a math course. It begins by defining optimization as the process of making something as effective as possible, which can range from improving study habits to enhancing car performance. The lecture then delves into how businesses and social services utilize optimization to maximize revenue and minimize costs, thereby increasing profits. Using mathematical procedures and derivatives, the course illustrates how to find optimum values. It also discusses the concept of absolute extrema in functions and how it applies to optimization, with examples involving different scenarios such as a hospital, police department, and a travel agency. The lecture includes practical problems, such as calculating the number of units that maximize revenue for a firm or the group size that maximizes revenue for a travel agency. It concludes with a problem on maximizing daily profit by determining the optimal number of units to sell and the corresponding selling price.
Takeaways
- 📈 **Optimization Definition**: Optimization is the process of making something better, more functional, or effective, which can be applied to various aspects like study habits or car performance.
- 💡 **Business Application**: Businesses aim to optimize revenue streams by maximizing revenue and minimizing costs to ultimately maximize profits.
- 🏥 **Healthcare Perspective**: Hospitals may optimize various factors such as minimizing post-surgery stays, infection rates, and legal issues like lawsuits.
- 👮 **Public Service Optimization**: Police departments might optimize community presence, crime rates, and officer recognition to improve their service.
- 🔍 **Absolute Extrema**: In mathematics, absolute extrema refer to the largest or smallest values of a function over its entire domain, which can be found using derivatives.
- 📉 **Domain Importance**: The domain of a function significantly impacts the absolute maximum and minimum values, which can change based on the specified range of X.
- 🔢 **Derivatives and Critical Values**: To find absolute extrema, one must consider both endpoint values and critical values where the derivative equals zero.
- 🧮 **Revenue Maximization**: For a business with a limited number of units sold per day, revenue maximization involves finding the number of units that yield the highest revenue.
- 💬 **Group Pricing Strategy**: A travel agency can maximize revenue by determining the optimal group size where the price per person decreases with each additional person over a base number.
- 📊 **Profit Maximization**: Profit is maximized when the number of units sold daily is the value that sets the derivative of the profit function to zero, indicating an optimal production level.
- 💰 **Optimal Selling Price**: The selling price at the optimal level of production can be determined by substituting the optimal number of units back into the price equation.
Q & A
What is optimization in the context of business and economics?
-Optimization is the process of making something better, more perfect, functional, or effective as possible. In business and economics, it often involves maximizing revenue and minimizing costs to increase profits.
How can optimization be applied in a hospital setting?
-In a hospital, optimization can involve minimizing the length of patient stays, reducing recovery times, lowering infection rates, and decreasing the number of lawsuits. It can also focus on the effectiveness of surgeries or therapies.
What is the difference between relative extrema and absolute extrema?
-Relative extrema are the highest or lowest points within a certain neighborhood of a function, whereas absolute extrema are the highest or lowest points over the entire domain of the function.
Why is it important to consider the domain when looking for absolute extrema?
-The domain limits the range of values that the function can take. Different domains can result in different absolute maxima and minima, as the function's behavior can change depending on the interval considered.
How does a business maximize revenue given a limited domain, such as a maximum number of units sold per day?
-The business would find the derivative of the revenue function, set it equal to zero to find critical points, and then compare these with the endpoints of the domain to determine where the revenue is maximized.
What is the revenue function for a travel agency that offers group tours with a price reduction for larger groups?
-The revenue function is derived from the price per person, which decreases as the group size increases beyond 25 people, multiplied by the number of people in the group. The function is R(x) = (25 + x)(300 - 10x), where x is the number of people above 25.
How does a company determine the number of units to sell to maximize profit, given a price function and a cost function?
-The company calculates the profit function by subtracting the total cost from the total revenue. It then takes the derivative of the profit function, sets it to zero to find the critical points, and uses the second derivative test to confirm that these points correspond to a maximum profit.
What is the second derivative test, and how is it used to determine if a critical point is a maximum?
-The second derivative test involves taking the derivative of the first derivative (the second derivative) of a function. If the second derivative at a critical point is negative, it indicates that the function is concave down at that point, which means the critical point is a local maximum.
How does the concept of optimization apply to a police department?
-A police department might optimize various aspects such as minimizing crime rates, maximizing community presence, or enhancing the effectiveness of community policing initiatives by assigning officers to specific areas.
What is the strategy for examining a function with a limited domain to find the absolute extrema?
-The strategy involves comparing both endpoint values and critical values (where the first derivative equals zero) within the specified domain to determine the absolute maximum and minimum values of the function.
How can the concept of optimization be used to improve study habits or car performance?
-Optimization can be applied to study habits by identifying the most effective study methods, times, and environments to maximize knowledge retention and grades. For car performance, it could involve optimizing the car's maintenance schedule or driving habits to maximize fuel efficiency and performance.
Outlines
📈 Introduction to Optimization in Business and Economics
The lecture begins by introducing optimization as a process that aims to improve various aspects of a system, such as study habits or car performance, to achieve better results. The focus then shifts to how businesses and social services apply optimization to maximize revenue and minimize costs, thereby increasing profits. The mathematical approach to finding optimal values using derivatives is also discussed, emphasizing the importance of understanding the concept of absolute extrema, which are the highest or lowest values of a function over its entire domain.
📉 Absolute Extrema and Their Significance in Optimization
The concept of absolute extrema is explored in detail, explaining that these are the highest or lowest values of a function across its entire domain. The lecture uses graphs to illustrate how absolute maxima and minima can be identified, and how the domain of a function can affect these values. It is emphasized that when evaluating a function with a limited domain, one must compare both endpoint values and critical values to determine the absolute extrema.
🔍 Identifying Critical Points and Endpoints for Optimization
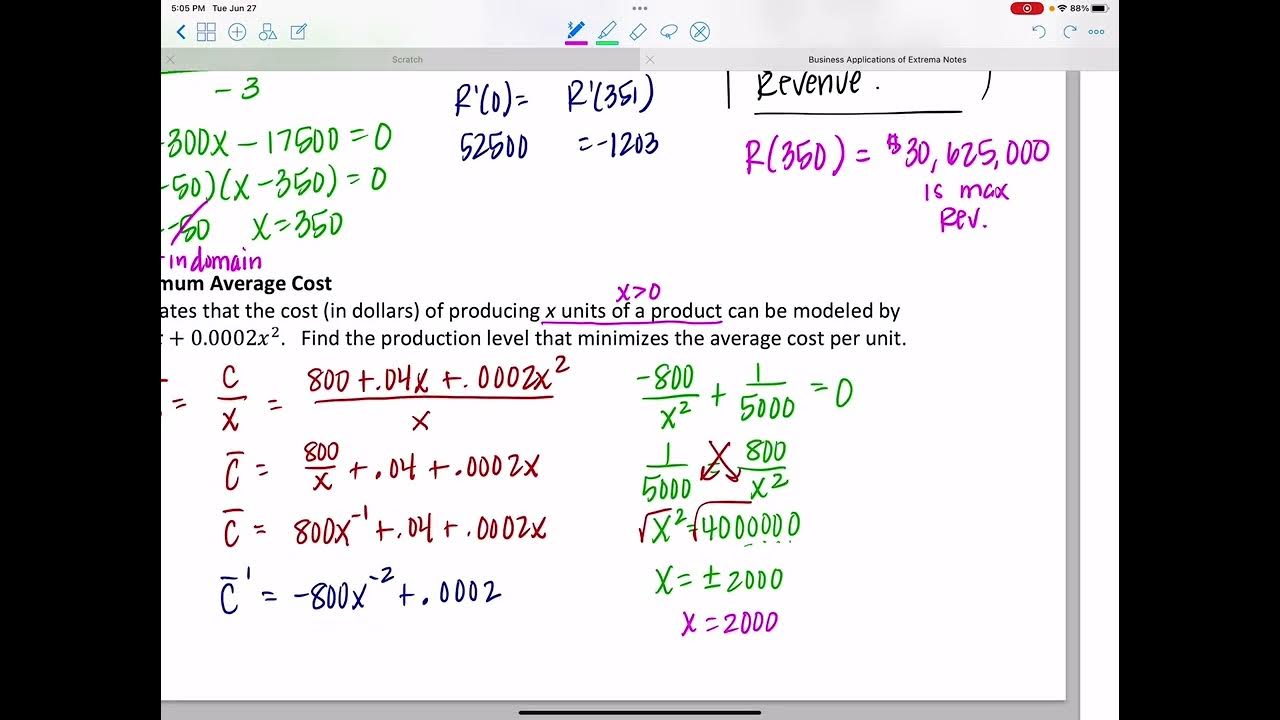
The process of identifying critical points, where the first derivative equals zero, and endpoints is explained as a method for finding the absolute extrema of a function. The importance of comparing these values to determine the maximum and minimum values of the function within a specified domain is highlighted. A step-by-step example is provided to demonstrate how to find the number of units that will maximize revenue for a firm, given a specific revenue function and domain constraints.
🧮 Maximizing Revenue: A Practical Example
A practical example involving a travel agency is used to illustrate the process of maximizing revenue. The agency's pricing structure is described, where the price per person decreases as the group size increases beyond 25 people. The goal is to find the group size that will produce the largest revenue for the agency. The lecture outlines the steps to create a revenue function based on the given pricing structure and then uses this function to determine the optimal group size.
📊 Revenue Function and Derivatives in Optimization
The construction of a revenue function based on the number of people in a group and the price per person is detailed. The lecture explains how to derive the revenue function and use it to find the critical values that maximize revenue. The process involves setting the derivative of the revenue function to zero and solving for the number of additional people (X), which leads to the optimal group size for maximizing revenue.
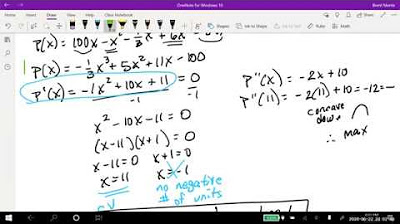
📉 Profit Maximization: Calculating Optimal Production Levels
The final paragraph focuses on maximizing profit by determining the optimal number of units to sell daily. The relationship between the price of a product and the number of units demanded is given, along with the average daily cost. The profit function is derived, and the process of finding the number of units that maximize profit is explained. The lecture concludes with the calculation of the selling price at the optimal level of production and the maximum possible daily profit.
Mindmap
Keywords
💡Optimization
💡Derivatives
💡Revenue
💡Costs
💡Profits
💡Absolute Extrema
💡Domain
💡Critical Values
💡Quadratic Equation
💡Second Derivative Test
💡Price Elasticity
Highlights
Optimization is an intuitive process used to make something better, more functional, or effective.
Businesses aim to optimize revenue streams by maximizing revenue and minimizing costs to increase profits.
Hospitals may optimize various factors, such as minimizing hospital stays, enhancing surgery effectiveness, and reducing infection rates.
Police departments can optimize community presence and face recognition to lower crime rates.
Absolute extrema are the largest or smallest function values over the entire domain of a function.
To find absolute extrema, one must compare both endpoint values and critical values where the derivative equals zero.
The domain of a function can significantly affect the absolute maximum and minimum values.
Derivatives are used to find critical values for optimization, indicating where the function's rate of change is zero.
The revenue function R(x) is used to determine the number of units that will maximize revenue, given a limited domain of sales.
For a travel agency, revenue maximization depends on the size of the group, with a price reduction for each additional person above twenty-five.
The profit function is derived from the revenue minus the average daily cost, aiming to find the quantity that maximizes profit.
The second derivative test is used to confirm whether an optimum value from the first derivative equals zero is a maximum or minimum.
The optimal selling price and the number of units to maximize profit are found by substituting the value back into the original equations.
The maximum possible daily profit is calculated by plugging the optimal number of units back into the profit equation.
It's important to pay attention to the specific question being asked, such as maximizing revenue versus finding the revenue amount.
The process of optimization involves identifying patterns and creating a general formula to apply to various scenarios.
In optimization problems, it's crucial to consider the practicality and constraints of the scenario, such as not being able to sell half units.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: