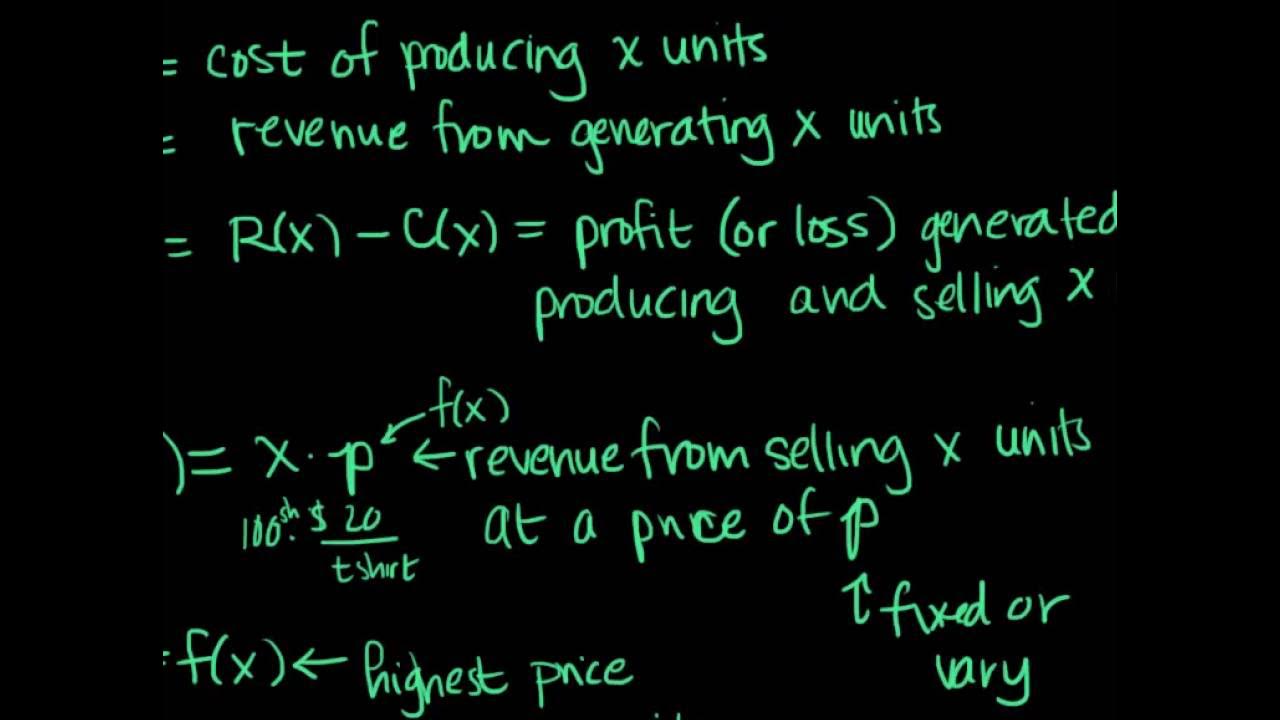Business Applications of Extrema
TLDRThis lesson delves into the business applications of finding extrema, focusing on maximizing or minimizing variables such as cost, revenue, and profit. The process involves using the first derivative test to identify critical points where the first derivative is zero or undefined. Key business functions like demand, cost, revenue, and profit are defined in terms of the number of units (x). The lesson covers calculating average cost, revenue, and profit by dividing the respective function by x. Examples illustrate how to find production levels that maximize revenue and minimize average cost using derivatives and critical point analysis. It also demonstrates deriving price functions from given data points and using them to maximize monthly revenue and profit. The summary emphasizes the importance of understanding the question, deriving the correct function, and providing the specific answer requested, whether it's the number of units, price, or another variable.
Takeaways
- 📈 Maximizing or minimizing business variables like cost, revenue, or profit involves finding extrema (maximum or minimum values).
- 🔍 The first derivative test is used to find critical points where the derivative is zero or undefined, indicating potential extrema.
- 📚 Functions such as demand, cost, revenue, and profit are essential in business applications and are expressed in terms of the number of units (x).
- 💰 Revenue is calculated as the price per unit times the number of units, and profit is the revenue minus the cost.
- 📊 To find averages like average cost, revenue, or profit, the respective function is divided by x, the number of units.
- 🔧 The process of finding extrema in business applications involves differentiating the relevant function and analyzing critical points.
- 🧮 For problems not directly providing a function, additional equations may need to be formulated using given data points.
- 📌 It's crucial to understand whether the question asks for the extremum value (like the number of units for max revenue) or the variable that produces that extremum (like the price for max profit).
- 🤔 Always consider the domain of the problem, for instance, the number of units produced and sold cannot be negative.
- 📝 After finding the critical point (x-value), plug it back into the original function to find the actual extremum value (like maximum revenue or profit).
- ⚖️ When given a scenario with multiple variables, such as price and quantity, use the information provided to express one variable in terms of another to create a function for differentiation.
Q & A
What is the primary goal when finding extrema in a business context?
-The primary goal is to find the maximum or minimum values of business-related metrics such as cost, revenue, or profit.
How is the first derivative test used to find extrema?
-The first derivative test involves finding critical numbers where the first derivative is either zero or undefined, which often correspond to local maxima or minima.
What are the different business functions discussed in the script?
-The script discusses demand function, cost function, revenue function, and profit function.
How is revenue calculated in the context of the script?
-Revenue is calculated as the price per unit multiplied by the number of units sold.
What is the formula for profit?
-Profit is calculated as revenue minus cost.
How can one find the average cost, revenue, or profit?
-To find the average, you take the respective function (cost, revenue, or profit) and divide it by the number of units X.
What is the significance of critical numbers in the context of finding maximum revenue?
-Critical numbers are the values of X where the derivative of the revenue function is zero or undefined. These points are potential candidates for maximum or minimum revenue.
How does the quadratic formula help in finding production levels for maximum revenue?
-The quadratic formula can be used to solve for X when the derivative of the revenue function (a quadratic equation) is set to zero, helping to find the production levels that yield maximum revenue.
What is the process to minimize the average cost of production?
-To minimize the average cost, you first find the derivative of the average cost function with respect to X, then solve for critical numbers where this derivative is zero.
In the context of the given script, how does a company maximize its monthly revenue by adjusting the price of its product?
-The company can maximize its monthly revenue by finding the price per unit that results in the maximum revenue function, which is derived from the relationship between price reduction and the increase in the number of units sold.
What is the final step after finding the extremum value of X in a business application problem?
-The final step is to plug the X value back into the original function (whether it's revenue, cost, or profit) to find the actual maximum or minimum value of the business metric.
Outlines
📈 Introduction to Business Applications of Extrema
The video begins with an introduction to the business applications of finding extrema, which are the maximum and minimum values of a function. The presenter explains the use of the first derivative test to identify these values in a business context, such as maximizing profit or minimizing cost. Key business functions like demand, cost, revenue, and profit are defined in relation to the number of units (X). The concept of average cost, revenue, and profit is also introduced, explaining how they are calculated by dividing the respective total function by X. An example of a cubic revenue function is provided to illustrate the process of finding the production level that yields maximum revenue.
🔍 Maximizing Revenue with a Given Production Level
The presenter discusses how to find the production level that maximizes revenue using the first derivative test. By differentiating the revenue function with respect to the number of items produced and sold (X), critical numbers are identified. The video demonstrates solving a quadratic equation to find the critical points and using the first derivative test to confirm that the critical point corresponds to a maximum revenue. The example provided involves a company with a cubic revenue function, and the process of finding the maximum revenue and the corresponding production level is shown step by step.
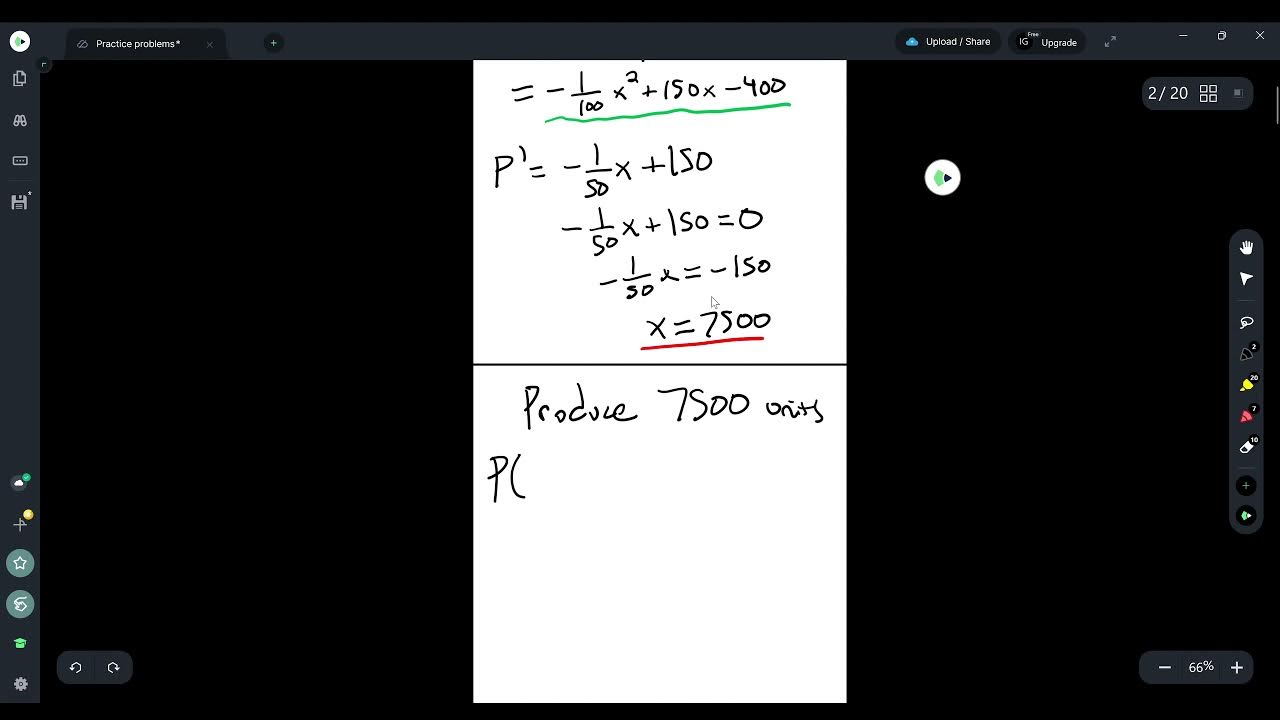
📉 Minimizing Average Cost with a Quadratic Cost Function
The focus shifts to finding the production level that minimizes the average cost of producing units. The presenter outlines the process of deriving the average cost function by dividing the total cost function by X and then differentiating it to find the minimum. The example given involves a quadratic cost function, and the presenter shows how to rewrite the average cost function, take its derivative, and solve for critical numbers to find the production level that minimizes the average cost. The domain of the problem is considered to ensure that the solution is applicable to the business context.
💹 Maximizing Monthly Revenue with Price and Demand Elasticity
The video tackles a more complex problem where the presenter must create equations based on given information to maximize monthly revenue. The business scenario involves a fixed number of units sold per month at a certain price, with the potential to sell more units with a price reduction. Using two points (price and quantity combinations), a price function is derived, which is then used to express revenue as a function of X. The presenter differentiates the revenue function to find the critical points and uses these to identify the price that maximizes monthly revenue. The process involves careful consideration of the relationship between price, quantity, and revenue.
📊 Maximizing Profit with a Given Demand and Cost Function
The final example is about maximizing profit, which requires creating a profit function from the given demand and cost functions. The presenter explains that profit is the difference between revenue (price times quantity) and cost. After expressing the profit function in terms of X, the derivative is taken to find the critical points that represent the maximum profit. The presenter shows how to solve for the critical points by setting the derivative equal to zero and using algebraic manipulation. The example involves a demand function that relates price to the square root of quantity and a linear cost function, leading to the determination of the price that yields maximum profit.
🎯 Conclusion and Assignment Advice
The presenter concludes by emphasizing the importance of understanding what is being maximized or minimized and focusing on the correct function to derive. They highlight that sometimes the answer involves plugging the critical value back into the original function to find the actual maximum or minimum value. The presenter offers help for further questions and encourages viewers to apply the concepts learned to their assignments, ensuring they read the questions carefully to provide the correct answer.
Mindmap
Keywords
💡Extrema
💡First Derivative Test
💡Demand Function
💡Cost Function
💡Revenue Function
💡Profit Function
💡Average Cost, Revenue, and Profit
💡Quadratic Formula
💡Critical Numbers
💡Maximizing and Minimizing
💡Price Function
Highlights
The lesson focuses on applying the process of finding extrema (maximum and minimum values) to business applications.
The first derivative test is used to find critical numbers for extrema in business-related functions such as cost, revenue, and profit.
Business applications involve maximizing or minimizing cost, revenue, profit, and understanding their relationships.
Functions such as demand, cost, revenue, and profit are defined in terms of the number of units (x) sold or produced.
Revenue is calculated as the price per unit multiplied by the number of units, and profit is revenue minus cost.
Average cost, revenue, or profit is found by dividing the respective function by the number of units (x).
The concept of average cost per item is illustrated using an example of spending on different items.
A cubic function is used to model total revenue, aiming to find the production level for maximum revenue.
The process involves differentiating the revenue function, finding critical numbers, and testing for maxima or minima.
The quadratic formula is applied to find the critical numbers where the derivative equals zero.
The domain of the problem is considered to ensure the solutions are applicable to the business context.
A company's cost function is used to find the production level that minimizes the average cost.
The derivative of the average cost function is taken and critical numbers are found to determine the minimum.
A business scenario is presented where the price per unit affects the number of units sold, and a price function is derived from given data points.
The revenue function is formulated based on the price function and the number of units sold, aiming to maximize monthly revenue.
A demand function is given, and the cost function is used to find the price that yields maximum profit.
Profit is maximized by finding the derivative of the profit function and solving for critical numbers.
The importance of carefully reading the question to ensure the correct answer is provided, whether it's the x-value or the calculated revenue/profit.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: