Math 1325 Lecture 9 9 - Applications
TLDRThis lecture explores the application of derivatives in understanding marginals in a business context. It defines marginals as incremental changes, such as marginal cost, revenue, and profit, which are critical for business decision-making. The lecture demonstrates how to calculate these marginals using derivatives of total cost, revenue, and profit functions. An example involves finding the marginal revenue from a monopoly market's demand function. The concept of optimization is introduced, where setting the derivative to zero helps find optimal production levels for maximizing profit. The lecture also discusses how to interpret the results in a practical context, emphasizing the importance of understanding the relationship between revenue, cost, and profit functions. It concludes with a practice problem on calculating marginal profit and analyzing profit changes at different production levels, highlighting the significance of the slope of revenue and cost functions in determining profit trends.
Takeaways
- 📈 Marginals represent small changes or increments such as marginal cost, revenue, and profit, which are crucial for businesses when considering the impact of producing or selling one more item.
- 💡 Marginal cost, revenue, and profit are found by taking the derivative of their respective total functions, as derivatives represent the instantaneous change in these functions.
- 📊 To find the marginal revenue at a specific quantity, you can use the derivative of the revenue function and evaluate it at that quantity.
- 🔍 The actual increase in revenue from selling one more item can be calculated by finding the revenue for one quantity and subtracting the revenue for one less quantity.
- 📌 The marginal revenue at a point is an estimate, and it helps businesses understand how the sale of an additional item affects revenue.
- 🔢 The concept of marginals is essential for decision-making and optimizing systems, such as maximizing profits or minimizing costs.
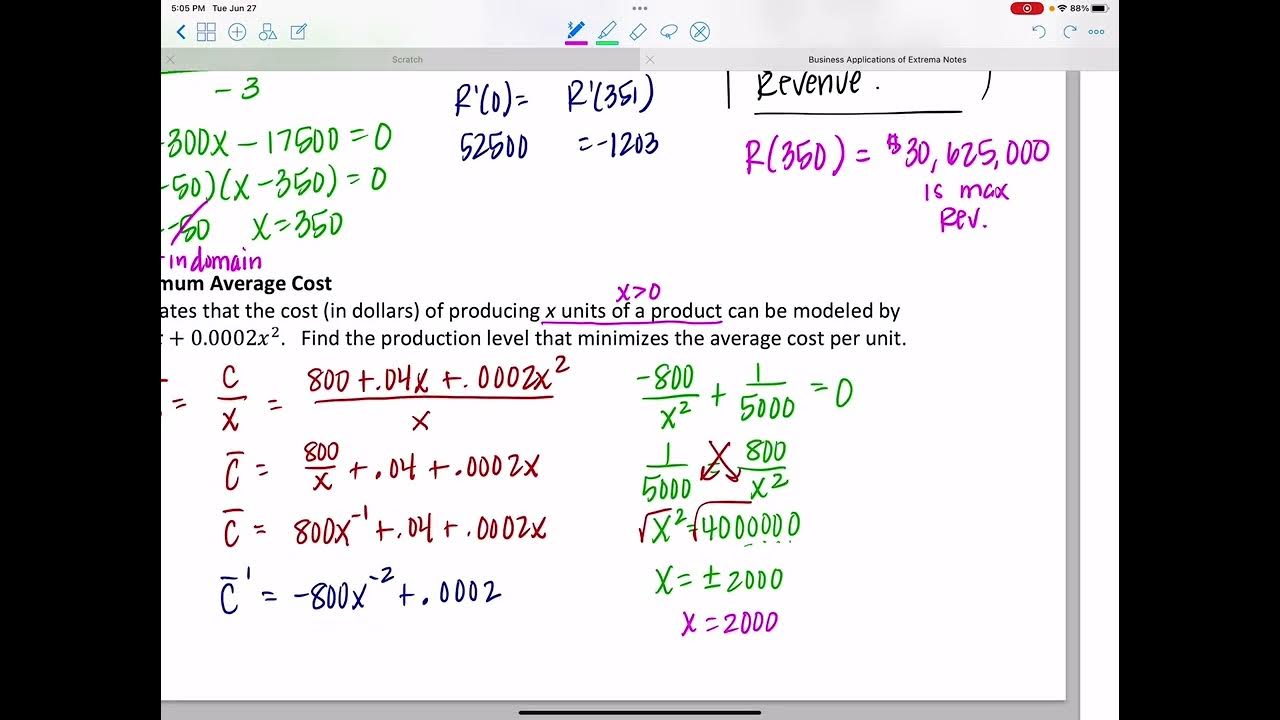
- 📉 The marginal revenue can help identify the optimal production level by looking at where the derivative (slope of the tangent line) is zero, which corresponds to the peak of the revenue function.
- 🤔 To determine if the next item will increase or decrease profit, compare the slopes of the revenue and cost functions; if the revenue slope is steeper, profits increase.
- 📚 Understanding the relationship between revenue, cost, and profit functions is vital for deriving the marginal profit function.
- 📉 A positive marginal profit indicates an increase in profit from selling an additional unit, even if the overall profit is still negative (i.e., a decrease in loss).
- 📈 The rate of change of profits can be increasing or decreasing, which can be determined by analyzing the slopes of the revenue and cost functions at different production levels.
Q & A
What is the definition of marginals in the context of business?
-Marginals in business refer to the cost, revenue, or profit associated with producing or selling one additional unit of a product. Specifically, marginal cost is the cost to produce one more item, marginal revenue is the revenue generated from selling one more item, and marginal profit is the profit generated from selling and making one more item.
How are marginals related to derivatives in mathematics?
-Marginals represent an incremental change in a specific function, such as cost, revenue, or profit. To find marginals, one calculates the derivative of the respective total function (e.g., total cost, revenue, or profit). The derivative represents the instantaneous change or rate of change, which in business terms translates to the marginal value.
What is the formula for total revenue given the demand function P = 16 - 0.02X?
-The total revenue is calculated as the product of the price (P) and the number of units (X) sold. Given the demand function P = 16 - 0.02X, the total revenue function R(X) is R(X) = P * X = (16 - 0.02X) * X = 16X - 0.02X^2.
How do you find the marginal revenue at X equals 40 for the given demand function?
-To find the marginal revenue at X equals 40, you first calculate the derivative of the total revenue function, which gives you the marginal revenue function. Then, you evaluate this function at X = 40. For the given function, the marginal revenue at X = 40 is calculated as 16 - 0.04 * 40 = $14.40.
What is the difference between the marginal revenue estimate and the actual increase in revenue when selling one more item?
-The marginal revenue estimate provides an approximation of the increase in revenue from selling one more item. The actual increase in revenue is found by calculating the revenue from selling X + 1 items and subtracting the revenue from selling X items. In the script's example, the marginal revenue estimate at X = 40 was $14.40, while the actual increase in revenue was $14.38, showing that the estimate was very close.
How does the concept of marginal revenue help in optimizing a system?
-Marginal revenue, as a derivative, represents the slope of the tangent line to the revenue function, which indicates the rate of change of revenue. By setting the derivative (marginal revenue) to zero and solving for the input value, one can find the point where the revenue is maximized or minimized, which is crucial for optimizing the system, such as maximizing profits or minimizing costs.
What is the marginal profit at a production level of 15 units given the total profit function P(X) = 20 * sqrt(X + 1) - 2X - 22?
-To find the marginal profit at X = 15, you take the derivative of the total profit function with respect to X, and then evaluate it at X = 15. The derivative of the given profit function is dP/dX = 20 * (1/2) * (X + 1)^(-1/2) - 2. Evaluating this at X = 15 gives a marginal profit of 10 / sqrt(16) - 2 = 1/2, which means an additional half-thousand dollars or $500 is earned from the 16th unit produced.
How is the marginal profit function derived from the revenue and cost functions?
-The marginal profit function is derived by first finding the revenue function (price times quantity) and the cost function (cost per unit times quantity). The profit function is then the difference between the revenue and cost functions. Taking the derivative of the profit function yields the marginal profit function, which represents the additional profit generated from selling one more unit.
What does the marginal profit function indicate about the change in profit when producing and selling an additional unit?
-The marginal profit function indicates whether the profit increases or decreases with the production and sale of an additional unit. If the marginal profit is positive, the profit increases with each additional unit sold. If it is negative, the profit decreases. A marginal profit of zero indicates that the profit does not change with the sale of an additional unit.
How can you determine whether the next item sold will increase or decrease the profit?
-To determine whether the next item sold will increase or decrease the profit, you compare the marginal revenue (the derivative of the revenue function) with the marginal cost (the derivative of the cost function). If the marginal revenue is greater than the marginal cost, the profit will increase with the sale of the next item. If the marginal cost is greater, the profit will decrease.
At what production level does the rate of change of profits start to decrease?
-The rate of change of profits starts to decrease when the slope of the cost function becomes steeper than the slope of the revenue function. In the script's example, this occurs around a production level of 1,000 units, indicating that the profits are no longer increasing as rapidly as before and the rate of profit growth is slowing down.
Outlines
📚 Introduction to Marginals and Derivatives in Business
This paragraph introduces the concept of marginals in the context of business and economics. It explains marginals as the cost, revenue, or profit associated with producing or selling one additional unit of a product. The paragraph also establishes the relationship between marginals and derivatives, illustrating how the derivative of a function can be used to find marginal costs, revenues, and profits. An example is provided where the demand function for a product at a monopoly market is given, and the total revenue function and marginal revenue at a specific quantity are calculated.
🔍 Calculating Actual vs. Estimated Revenue Increases
The second paragraph delves into the difference between estimating and calculating the actual increase in revenue from selling an additional item. It demonstrates how by finding the revenue for 41 items and subtracting the revenue for 40 items, one can determine the precise revenue increase from selling the 41st item. The paragraph emphasizes the importance of using marginal revenue for decision-making in business due to its simplicity and efficiency over more complex calculations. It also visually describes how marginal revenue can be used to optimize systems by setting the derivative to zero to find the maximum or minimum value of a function.
📈 Deriving Marginal Profit and Analyzing Profit Functions
This paragraph focuses on the concept of marginal profit, which is the additional profit generated from producing and selling one more unit. It guides through a practice problem where the total profit function is given, and the marginal profit at a specific production level is calculated using derivatives. The explanation includes the application of the chain rule in differentiation. The paragraph concludes with an interpretation of the marginal profit result, emphasizing the importance of understanding the unit of measure in the context of the problem.
💰 Understanding Profit Functions and Breakeven Points
The final paragraph discusses how to derive the marginal profit function from given cost and revenue functions. It explains the process of calculating the revenue, cost, and profit functions and then finding the derivative of the profit function to obtain the marginal profit. The paragraph uses a graph to illustrate how the slopes of the revenue and cost functions can indicate whether selling an additional unit will increase or decrease profit. It also clarifies a common misconception about profit increase, explaining that an increase in profit does not necessarily mean a positive profit, but rather a decrease in the amount of loss. The concept of breakeven is introduced, and the paragraph concludes with an analysis of profit changes at different production levels.
Mindmap
Keywords
💡Marginal
💡Derivative
💡Total Revenue Function
💡Marginal Revenue
💡Total Cost Function
💡Profit Function
💡Optimization
💡Chain Rule
💡Breakeven Point
💡Competitive Market
💡Instantaneous Change
Highlights
Marginals are defined as something situated on the margin or edge, representing a small change.
In business, marginal cost is the cost to produce one more item, marginal revenue is the revenue from selling one more item, and marginal profit is the profit from selling and making one more item.
Marginals are found by taking the derivative of the respective functions, such as total cost, revenue, or profit functions.
Marginal profit can also be calculated as the derivative of revenue minus the derivative of cost, since profit equals revenue minus cost.
The concept of marginals is used to estimate the instantaneous change when producing or selling an additional item.
Total revenue function is calculated as price times the number of items sold (P*X), and marginal revenue is the derivative of this function.
An example problem demonstrates how to find the total revenue function and marginal revenue at a specific quantity.
Marginal revenue at a specific point estimates the revenue increase from selling one more item, which is useful for business decision-making.
The actual increase in revenue from selling an additional item can be found by subtracting the revenue of one quantity from the next.
Optimizing involves maximizing or minimizing a system, often profits or efficiency, and can be visualized graphically with the help of a total revenue function graph.
The marginal revenue at the maximum revenue point is equal to zero, indicating the peak of the revenue function.
Setting the derivative equal to zero helps find the optimum value for maximizing or minimizing a function.
An example practice problem illustrates how to calculate marginal profit at a specific production level using derivatives.
Marginal profit represents the additional profit from selling one more unit and is calculated in the same unit as total profit.
The marginal profit function is derived from the profit function, which is the difference between the revenue and cost functions.
Graphical analysis of the profit function can help determine whether the next item sold will increase or decrease profit based on the slopes of the revenue and cost functions.
Profits can increase even when the cost is above the revenue if the rate of decrease in loss is significant, indicating a move towards breakeven or profitability.
At certain production levels, the rate of change of profits can be determined by comparing the slopes of the revenue and cost functions to decide if the next item sold will increase profits.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: