Business Calculus - Section 3.4 - Optimization and Elasticity of Demand
TLDRThe video script delves into the critical concept of optimization in business calculus, focusing on finding the maximum or minimum values of a function to maximize profit and minimize cost. It introduces the extreme value theorem, which states that a continuous function on a closed interval will achieve its absolute extrema at a critical number or an endpoint. The script guides through several examples to illustrate how to find absolute extrema for different functions, using both graphical and algebraic methods. It also explores the second derivative test for absolute extrema, which is particularly useful when there is a unique critical point. The video further applies these concepts to business scenarios, such as determining the production quantity for maximum profit and minimum average cost, and concludes with an examination of the price elasticity of demand, explaining how it measures the sensitivity of demand to price changes and its implications for revenue. The script is a comprehensive resource for understanding optimization in a business context.
Takeaways
- 📈 **Optimization in Business**: The process of finding the maximum or minimum values of a function is crucial in business for maximizing profit and minimizing costs.
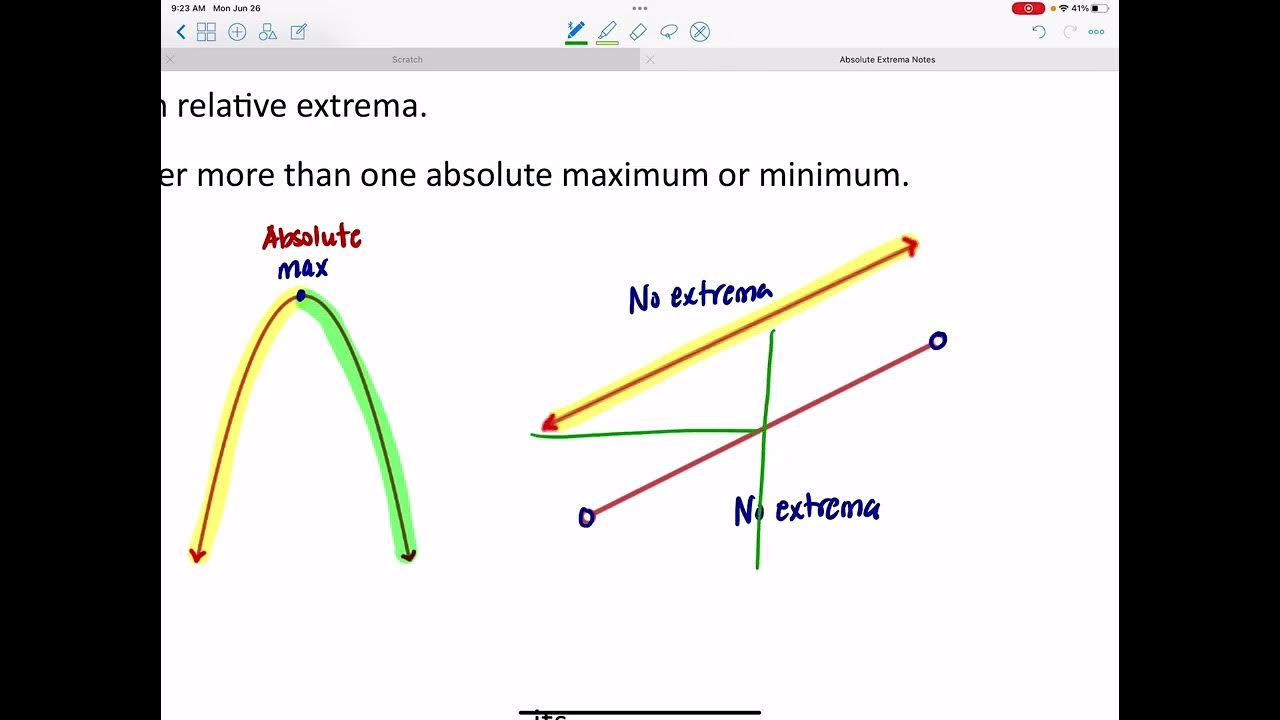
- 📉 **Absolute Extrema**: The absolute maximum or minimum of a function over its entire domain is unique (if it exists) and can occur at multiple points along the domain.
- 📊 **Extreme Value Theorem**: A continuous function on a closed interval achieves its absolute extrema at a critical number or an endpoint of the interval.
- 🔍 **Graphical Analysis**: Visual inspection of a function's graph can help identify absolute extrema, though it requires the function to have a bounded domain.
- 🧮 **Derivatives and Critical Values**: To find absolute extrema, calculate the first derivative, find critical values by setting the derivative to zero, and then evaluate the endpoints and critical points.
- 📌 **Second Derivative Test**: If a function has a single critical point and the second derivative at that point is positive, it indicates an absolute minimum; if negative, an absolute maximum.
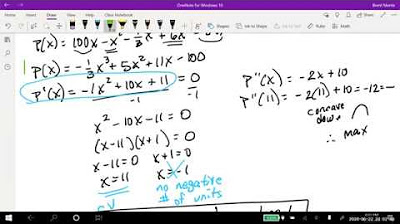
- 💰 **Profit Maximization**: In business, the profit function is revenue minus cost, and maximizing profit involves finding the production quantity that results in the highest profit.
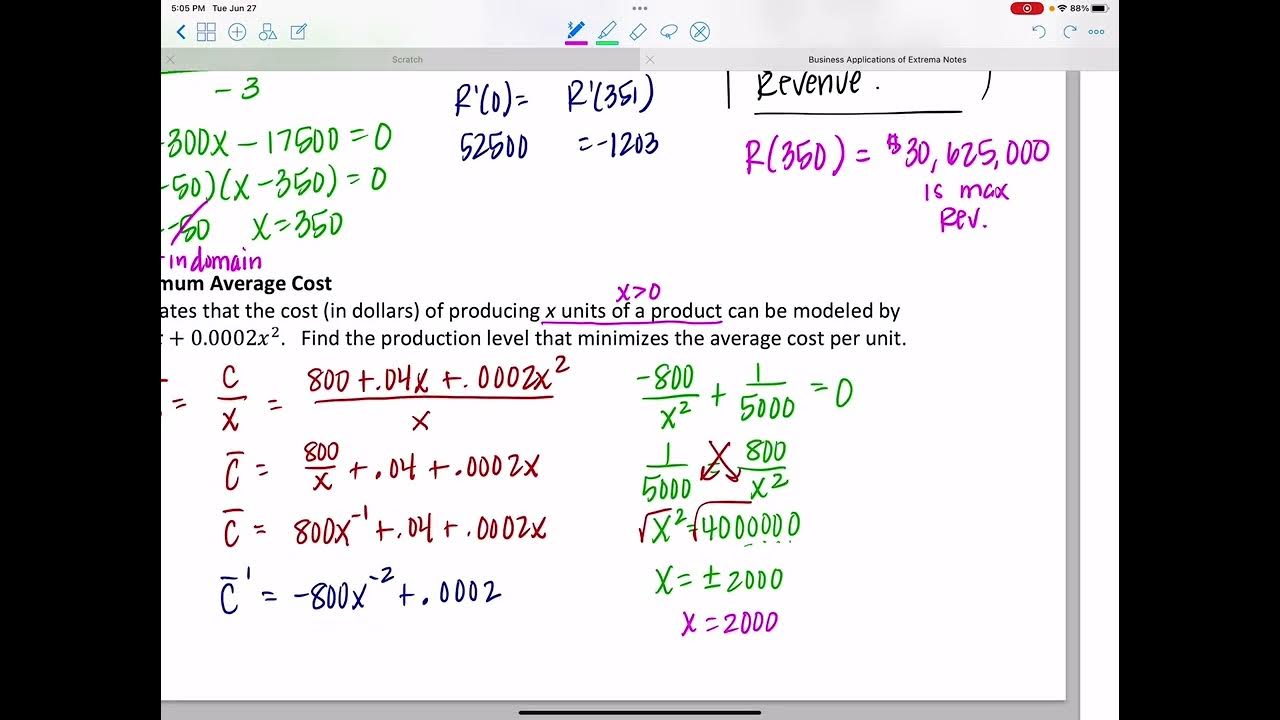
- 📐 **Average Cost Minimization**: The average cost (AC) is the total cost divided by the quantity produced, and minimizing AC can be achieved by finding the critical points of the AC function.
- 📉 **Elasticity of Demand**: A measure of how sensitive the quantity demanded is to a change in price, given by the percentage change in quantity demanded divided by the percentage change in price.
- 📈 **Revenue and Elasticity**: Revenue is maximized at the price where demand is at unit elasticity, which is when the elasticity of demand equals 1.
- 📈 **Price and Elasticity**: When demand is inelastic (elasticity < 1), a price increase results in a proportionally smaller decrease in quantity demanded, leading to increased revenue.
Q & A
What is optimization in business calculus?
-Optimization in business calculus is the process of finding the maximum or minimum values of a function. In business, this often involves finding the maximum profit with a minimum cost or minimum average cost.
What is the difference between absolute maximum and relative maximum?
-The absolute maximum is the largest Y value that a function takes on over its entire domain, and it is unique if it exists. A relative maximum, on the other hand, can occur at multiple points and is not the largest Y value over the entire domain but is a local maximum in a certain interval.
What is the extreme value theorem?
-The extreme value theorem states that a function f of X that is continuous on a closed interval A to B obtains its absolute extrema at either a critical number inside the open interval from A to B or at an endpoint of the interval from A to B.
How is the derivative used to find critical values?
-The derivative of a function is set equal to zero to find critical values. These values are potential points where the function could have a maximum or minimum, and they are used to analyze the behavior of the function.
What is the elasticity of demand?
-The elasticity of demand measures how responsive or sensitive demand is to changes in price. It is calculated using the formula E(P) = (-dQ/dP * P) / Q, where Q is the quantity demanded and P is the price.
How does the second derivative test for absolute extrema work?
-The second derivative test for absolute extrema is used when there is only one critical number. If the second derivative at this point is positive, the function has an absolute minimum at that point. If the second derivative is negative, the function has an absolute maximum at that point.
What is the significance of finding the maximum profit in a business context?
-Finding the maximum profit is significant in a business context as it helps a company determine the optimal production levels and pricing strategies to maximize earnings while minimizing costs.
How is the average cost function used to find the minimum average cost?
-The average cost function is created by dividing the total cost function by the number of units produced. The derivative of this function is taken and set to zero to find the critical points. Using the second derivative test or analyzing the behavior of the function helps determine if a minimum average cost exists and at what production level it occurs.
What are the different types of demand elasticity?
-There are three types of demand elasticity: inelastic demand (when elasticity is less than 1), unitary elasticity (when elasticity equals 1), and elastic demand (when elasticity is greater than 1). These types indicate the degree to which demand responds to price changes.
How does the revenue function relate to the price and quantity demanded?
-The revenue function is the product of the price and the quantity demanded at that price. It is used to determine the total income generated from sales and can be analyzed to find the price that maximizes revenue.
What is the relationship between the price elasticity of demand and the revenue function?
-The price elasticity of demand indicates how sensitive the quantity demanded is to a change in price. When demand is inelastic, increasing the price will lead to an increase in revenue. When demand is elastic, increasing the price will lead to a decrease in revenue. At unitary elasticity, the revenue is at its maximum.
Outlines
📈 Introduction to Optimization in Business Calculus
The video introduces the concept of optimization in the context of business calculus. It discusses how optimization is used to find the maximum profit and minimum cost or average cost for a business. The focus is on the extreme value theorem and applying these principles to real-world business and economic situations. The video also mentions the concept of elasticity of demand, which measures the relationship between price and demand changes.
📉 Absolute Extrema and the Extreme Value Theorem
This paragraph explains the concept of absolute extrema, which refers to the highest (absolute maximum) and lowest (absolute minimum) values that a function can take within its domain. The extreme value theorem is introduced, stating that a continuous function on a closed interval will achieve both a maximum and a minimum at either a critical point or an endpoint of the interval. The video provides examples to illustrate the application of the theorem and discusses scenarios where the theorem does not apply.
🔢 Finding Absolute Extrema for Specific Functions
The video presents an example of finding the absolute extrema for a given function within a closed interval. It demonstrates how to find critical points and endpoints, and then determine which of these points correspond to the absolute maximum or minimum values. The process involves taking derivatives, solving for critical values, and evaluating the function at these points. The extreme value theorem is used to guarantee the existence of extrema within the given interval.
📚 Second Derivative Test for Absolute Extrema
The paragraph discusses the second derivative test, which is a method to determine whether a critical point is an absolute maximum, minimum, or neither. It explains that if the second derivative is positive at a critical point, the function has an absolute minimum at that point, and if the second derivative is negative, the function has an absolute maximum. The video provides an example using the second derivative test to find the absolute maximum of a function.
📊 Business Application: Maximizing Profit and Minimizing Average Cost
The video applies the concepts of optimization to a business scenario. It outlines how to calculate the profit function and use it to determine the quantity of products that should be produced to maximize profit. The video also shows how to calculate the average cost and find the quantity that minimizes the average cost. The second derivative test is used to confirm the absolute maximum for profit and the minimum average cost.
📉 Elasticity of Demand and Its Application
The video concludes with a discussion on the elasticity of demand, which measures the responsiveness of the quantity demanded to changes in price. The formula for calculating the price elasticity of demand is provided, and the video explains how to interpret different elasticity values (elastic, inelastic, and unitary). The video also demonstrates how to graph the revenue function and identify regions of elastic and inelastic demand, as well as the point of maximum revenue corresponding to unitary elasticity.
Mindmap
Keywords
💡Optimization
💡Absolute Extrema
💡Extreme Value Theorem
💡Elasticity of Demand
💡Derivative
💡Continuous Function
💡Critical Points
💡Second Derivative Test
💡Profit Function
💡Average Cost
💡Revenue Function
Highlights
Optimization is a key concept in business calculus, focusing on finding maximum or minimum values of a function to maximize profit and minimize costs.
The extreme value theorem states that a continuous function on a closed interval obtains its absolute extrema at a critical number or an endpoint of the interval.
Absolute extrema are unique Y values for a function over its entire domain, differing from relative maxima which can occur multiple times.
Graphical analysis of functions can help identify absolute minima and maxima by observing the lowest and highest Y values within a bounded domain.
The elasticity of demand measures the responsiveness of demand to changes in price, crucial for understanding how price adjustments affect sales.
The price elasticity of demand is calculated using the formula E(P) = (-dQ/dP * P) / Q, where Q is the quantity demanded and P is the price.
Inelastic demand occurs when the percentage decrease in quantity demanded is less than the percentage increase in price.
Unitary elasticity signifies that a 1% increase in price results in a 1% decrease in quantity demanded.
Elastic demand is identified when the percentage decrease in quantity demanded is greater than the percentage increase in price.
The revenue function, R(P) = P * Q(P), represents the total revenue generated from sales at a given price level.
The maximum revenue point coincides with the unitary elasticity of demand, where demand is equally responsive to price changes.
The second derivative test for absolute extrema is a powerful tool to determine if a critical point is an absolute maximum or minimum.
A profit function is derived from revenue minus cost, and its maximum value indicates the optimal production level for maximum profit.
The average cost function can be minimized by finding the critical points and applying the second derivative test to ensure a minimum average cost.
Business applications of calculus involve optimizing production levels and pricing strategies to increase profit and minimize costs.
The concept of absolute extrema is graphically represented by the highest and lowest points on a function's graph within a specific domain.
The domain's nature (open or closed) affects the applicability of the extreme value theorem and the identification of absolute extrema.
The second derivative test is used to confirm whether a critical point is an absolute maximum or minimum by assessing concavity.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: