Math 11 - Section 3.5
TLDRIn this video, Professor Monty delves into the application of calculus to economic problems, specifically focusing on optimizing profit in business scenarios. The video begins by illustrating how to find absolute maximum and minimum values, which are then applied to determine the maximum profit for a given revenue and cost function. The professor guides viewers through a step-by-step process, starting with the basic formula for profit (revenue minus cost) and proceeding to find critical points by setting the derivative of the profit function to zero. The video emphasizes the importance of verifying these critical points as maximum or minimum values using either the first or second derivative test. The professor demonstrates this process with three different economic problems, each increasing in complexity. The first problem involves finding the maximum profit and the number of units to produce for a given revenue and cost function. The second problem adds an additional layer by also determining the price that maximizes profit. The third problem is a more complex application involving a university's decision on ticket pricing for football games, taking into account variable attendance and concession sales. Throughout the video, the professor stresses the importance of understanding each step in the process and provides clear explanations to ensure comprehension. The video concludes with a reminder to practice these techniques, as they are essential for solving optimization problems in economics.
Takeaways
- 📈 Maximizing profit in a business context involves finding the absolute maximum value, which can be applied to economic problems.
- 💰 Profit is calculated as revenue minus cost, and the goal is to maximize this profit function regarding the variable x, which represents thousands of units.
- 🔍 To find the maximum profit, first set up the profit function, then take its derivative and set it equal to zero to find critical values.
- 📌 After finding critical values, verify them as maximums by using either the first derivative test or the second derivative test.
- ✅ When using the second derivative test, a negative second derivative indicates a concave down graph, which confirms a maximum at the critical value.
- 🔢 In the context of the given problems, the revenue function and cost function are provided, and the profit function is derived from these.
- 📉 The first derivative of the profit function gives the critical points where the profit could be maximized or minimized.
- 🤔 It's important to remember that a critical point is not automatically a maximum; it must be verified through a derivative test.
- 📚 The script provides a step-by-step guide through multiple problems, emphasizing the process of optimization in economic scenarios.
- 🏛️ An example problem involves a university maximizing revenue from football game tickets by adjusting ticket prices and considering attendance variables.
- 💡 The process of optimization is not just about finding a critical point but also about understanding the context and applying the correct mathematical tests to verify the maximum.
- ⚖️ Always consider the practical implications of the solution, such as whether the number of units produced or the number of attendees fits within real-world constraints.
Q & A
What is the main topic of the lecture?
-The main topic of the lecture is the application of finding absolute maximum and minimum values to economic problems, specifically focusing on business and economic applications.
What is the formula for profit in the context of the lecture?
-The formula for profit is revenue minus cost, where both revenue and cost are given in thousands of dollars, and the number of units (x) is in thousands.
How does Professor Monty approach the first problem in the lecture?
-Professor Monty approaches the first problem by first identifying the revenue and cost functions, then deriving the profit function, and finally using calculus to find the critical points that represent potential maximum profit.
What is the significance of finding the second derivative of the profit function?
-The second derivative of the profit function is significant because it helps to determine whether a critical point is a maximum, minimum, or an inflection point. If the second derivative is negative, it indicates that the function is concave down at that point, which means it is a maximum.
Why is it important to verify the critical value found?
-It is important to verify the critical value found because simply finding a critical point does not guarantee that it corresponds to a maximum or minimum value. Verification using either the first derivative test or the second derivative test confirms the nature of the critical point.
What is the role of the price function in determining the revenue?
-The price function is used to calculate the revenue by multiplying the price per unit by the quantity sold. In the context of the lecture, the price function is given as a function of x, which represents the quantity of suits sold.
How does the number of units produced (x) affect the profit in the second problem?
-In the second problem, the number of units produced (x) directly affects the profit as it is part of both the revenue and cost functions. The goal is to find the value of x that maximizes the profit function, which is done by finding the critical points of the profit function.
What is the strategy for solving the third problem regarding ticket pricing for football games?
-The strategy for solving the third problem involves setting up a revenue function that includes both ticket sales and concession revenue, then using calculus to find the critical points of this function to determine the price per ticket that maximizes revenue.
Why is it necessary to consider the stadium's capacity when deciding on the number of tickets to sell?
-It is necessary to consider the stadium's capacity to ensure that the number of tickets sold does not exceed the number of people the stadium can accommodate. If the capacity is exceeded, it could lead to safety issues and a negative experience for attendees.
How does the change in ticket price affect the average attendance?
-According to the script, every decrease of three dollars to the ticket price adds ten thousand people to the average attendance. This relationship is used to calculate the quantity of tickets sold as part of the revenue function.
What is the final step in solving each of the problems presented in the lecture?
-The final step in solving each problem is to verify that the critical value found corresponds to a maximum profit. This is done by either using the first derivative test or the second derivative test to confirm that the point is indeed a maximum.
Outlines
📚 Introduction to Economic Optimization
Professor Monty begins the lecture by reminding the audience of the previous discussion on finding absolute maximum and minimum values. The focus of today's lecture is to extend this knowledge to economic problems, specifically looking at optimization in business and economic contexts. The section, 3.5, is about finding absolute maximum and minimum values for business applications. The first problem involves finding the maximum profit by analyzing a given revenue function and cost function, where both are measured in thousands of dollars, and the number of units, x, is also in thousands. The goal is to maximize profit, which is calculated as revenue minus cost.
🔢 Profit Maximization through Derivatives
The process of finding the maximum profit involves setting up the profit function as revenue minus cost and then finding its derivative. The derivative of the profit function is set to zero to find critical values. After simplifying the derivative, two potential solutions for x are found: x = 11 and x = -1. Since negative units of production are not feasible, x = 11 is chosen as the critical value. To confirm that this is a maximum, the second derivative test is used. The second derivative of the profit function at x = 11 is negative, indicating a maximum. Therefore, producing 11,000 units is concluded to maximize the profit.
📈 Calculating Maximum Profit and Price
The next step is to calculate the maximum profit by substituting x = 11 into the original profit function. The calculation yields a repeating decimal, which is then multiplied by 1000 to reflect the profit in thousands of dollars. The maximum profit is found to be $182,333. The problem then shifts to a clothing firm scenario where the price and cost functions are given, and the task is to find the total revenue, total profit, the number of units to produce for maximum profit, and the price that will maximize profit. The revenue function is derived from the given price function, and the profit function is calculated by subtracting the cost function from the revenue function.
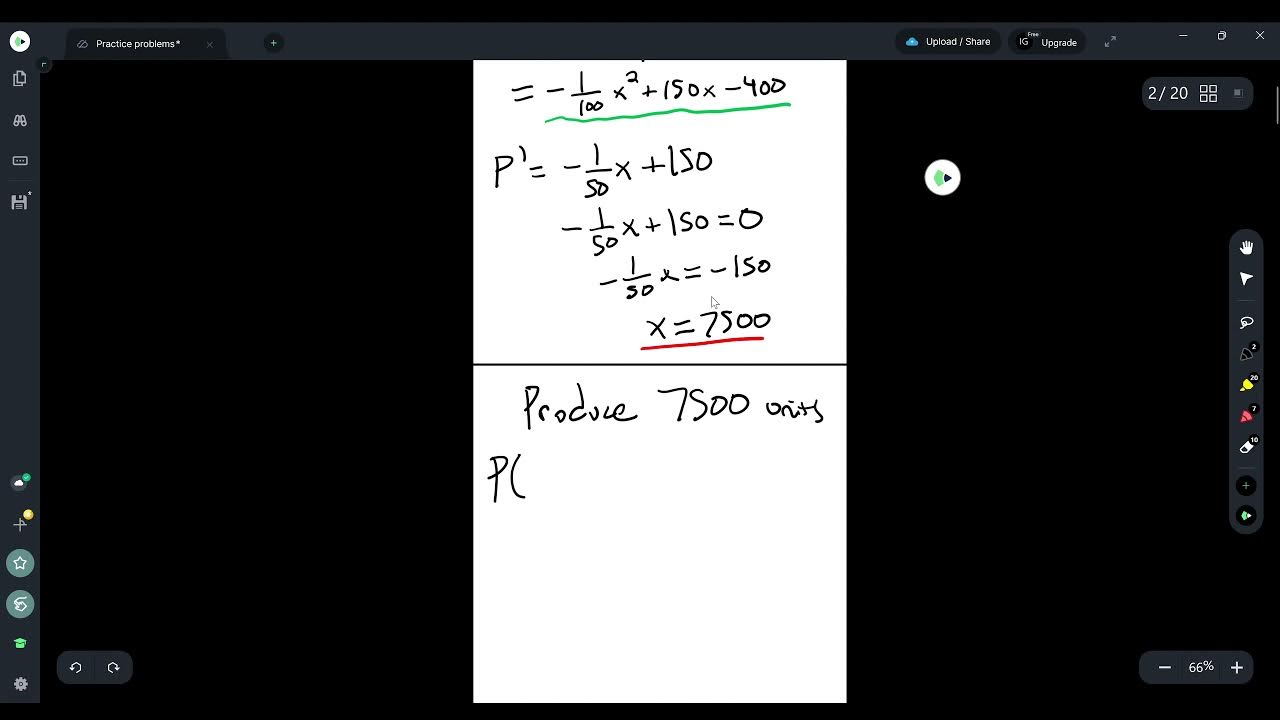
📉 Finding the Optimal Number of Suits to Produce
To find out how many suits need to be produced and sold to maximize profit, the derivative of the profit function is taken and set to zero. The critical value obtained is x = 100, which is verified to be a maximum using the second derivative test. The maximum profit is then calculated by substituting x = 100 into the profit function, resulting in a maximum profit of $3,500. The price that should be set per suit to maximize profit is also found by substituting x = 100 into the given price function, resulting in a price of $100 per suit.
🏈 Maximizing Revenue for Football Game Tickets
The final problem involves a university looking to maximize revenue from football game tickets. The current ticket price is $18, and for every $3 decrease in ticket price, attendance increases by 10,000 people. The revenue function is constructed by considering the ticket price, the number of attendees, and the additional revenue from concessions. The problem is to find the price per ticket that will maximize revenue and the corresponding number of attendees. The revenue function is derived, and the derivative is taken to find critical values. The critical value x = 1.75 is found, and it is verified to be a maximum using the second derivative test.
🎟️ Determining the Optimal Ticket Price and Revenue
The optimal ticket price is calculated by substituting the critical value x = 1.75 into the price function, resulting in a price of $12.75 per ticket. The number of tickets that would be sold at this price is determined by adding the increase in attendance (10,000 times 1.75) to the original 40,000 attendees, resulting in 57,500 tickets. The maximum revenue is then calculated by substituting x = 1.75 into the revenue function, yielding a revenue of $991,875. This not only exceeds the original revenue but also implies a higher profit due to reduced costs associated with a larger attendance.
📝 Conclusion and Importance of Verification
The lecture concludes with a reminder of the importance of verifying critical values using either the first or second derivative test to ensure that they represent a maximum. The process is emphasized as essential for confirming that the calculated values indeed lead to the maximum profit or revenue. The professor encourages practice and perseverance, highlighting that the problems are applications of concepts previously learned.
Mindmap
Keywords
💡Absolute Maximum
💡Revenue Function
💡Cost Function
💡Profit Function
💡Derivative
💡Critical Values
💡Second Derivative Test
💡Quadratic Function
💡Fixed Costs
💡Optimization
💡Price Elasticity
Highlights
Professor Monty introduces the concept of applying calculus to economic problems to find absolute maximum and minimum values.
The first problem involves finding the maximum profit by analyzing revenue and cost functions.
Revenue is defined as money coming in, and cost is the money spent to produce or purchase items.
The profit function is derived by subtracting the cost function from the revenue function.
To maximize profit, the derivative of the profit function is taken and set to zero to find critical values.
The second derivative test is used to confirm that a critical value is a maximum by checking if it's concave down.
The maximum profit is found by evaluating the profit function at the critical value where the derivative is zero.
In the second problem, the focus shifts to a clothing firm determining the optimal price and production quantity to maximize profit.
The revenue function is derived from the given price function, highlighting the relationship between price and quantity sold.
The profit function is simplified by combining like terms and ensuring the constant term represents fixed costs.
The number of units to produce for maximum profit is determined by solving the profit function's derivative.
The maximum profit is calculated by substituting the optimal number of units into the profit function.
The third problem involves a university maximizing revenue from football game tickets by adjusting ticket prices.
The revenue function includes both ticket sales and concessions, with the price and attendance varying based on the number of price drops.
The optimal ticket price is found by differentiating the revenue function with respect to the number of price drops and solving for zero.
The maximum revenue is calculated, and it's noted that costs may decrease with increased attendance, potentially increasing profit.
The importance of verifying the maximum using either the first or second derivative test is emphasized to ensure the critical value corresponds to a maximum.
The process is summarized as an application of previously learned calculus concepts to solve real-world economic problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: