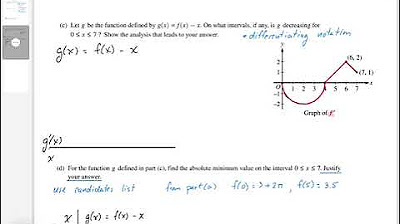2022 AP Calculus AB BC Free Response #3
TLDRThe video transcript discusses a mathematical problem involving a differentiable function, f, with a given value at x=4 and a graph consisting of a semicircle and two line segments. The presenter outlines a step-by-step approach to find the values of f at x=0 and x=5 using the Fundamental Theorem of Calculus. The problem also involves identifying points of inflection, which are determined by the sign changes of the second derivative of f. Additionally, a function g(x) is defined as g(x) = f(x) - x, and the presenter explains how to find the intervals where g is decreasing by analyzing the sign of g'(x). Finally, the absolute minimum value of g on the interval [0, 7] is sought by evaluating g at critical points and endpoints, resulting in the minimum value being identified.
Takeaways
- 📌 The problem involves a differentiable function f with a known value at x=4 and a graph of its derivative f' consisting of a semicircle and two line segments.
- 🧮 To find f(0) and f(5), the speaker uses integration of f' from 0 to 4 and from 4 to 5, respectively, applying the Fundamental Theorem of Calculus.
- 🔍 The area under the curve of f' from 0 to 4 is calculated to be -2π, which helps in determining f(0).
- 🔢 f(0) is found by rearranging the equation to f(0) = 3 + 2π, after integrating from 0 to 4.
- 🚀 For finding f(5), the area from 4 to 5 is a triangle with base and height of 1, leading to an area of 1/2, thus f(5) = 3 + 1/2.
- 🤔 Points of inflection are determined by where the second derivative, f'', changes signs, which is identified at x=6.
- 📈 The function g(x) = f(x) - x is analyzed to find intervals where it is decreasing, which involves finding where g'(x) < 0.
- 📉 g'(x) is calculated as f'(x) - 1, and the intervals where it is less than zero are between 0 and 5.
- 🔑 The critical points for g(x) are identified at x=5 and x=7, with only x=5 being relevant for the interval in question.
- 📐 The absolute minimum value of g(x) on the interval is sought by evaluating g at the endpoints and the critical point.
- 📨 g(0), g(5), and g(7) are computed, with g(0) = 3 + 2π, g(7) = -1/2, and g(5) = -3/2.
- 🏁 The absolute minimum value of g(x) on the interval [0, 7] is identified to be -3/2, which occurs at x=5.
Q & A
What is the value of f(4) given in the transcript?
-The value of f(4) is given as 3.
What is the shape of the graph of f'(t)?
-The graph of f'(t) consists of a semicircle and two line segments.
How is f(0) calculated in the transcript?
-f(0) is calculated by integrating from 0 to 4 of f'(t) dt, which equals f(4) - f(0), and then solving for f(0) to get 3 + 2π.
What is the value of f(5) according to the transcript?
-f(5) is calculated by integrating from 4 to 5 of f'(t) dt, which equals f(5) - f(4), and found to be 3 + 1/2 = 7/2 or 3.5.
At what x-coordinate is the point of inflection located?
-The point of inflection is located at x equals 6, as this is where the second derivative, f''(x), changes signs.
Define the function g(x) as given in the transcript.
-The function g(x) is defined as g(x) = f(x) - x.
On what intervals is the function g(x) decreasing?
-g(x) is decreasing on the interval from 0 to 5.
How are the critical points for g(x) found?
-The critical points for g(x) are found by determining where g'(x) = 0, which occurs at x = 5.
What are the values of g(x) at x = 0, 5, and 7?
-g(0) is 3 + 2π, g(5) is -3/2, and g(7) is -1/2.
What is the absolute minimum value of g(x) on the interval from 0 to 7?
-The absolute minimum value of g(x) on the interval from 0 to 7 is -3/2, which occurs at x = 5.
How is the area under the curve of f'(t) from 0 to 4 calculated?
-The area is calculated by integrating f'(t) dt from 0 to 4, which represents the negative area because it's below the x-axis, and is found to be -2π.
What is the significance of the second derivative in finding points of inflection?
-The second derivative, f''(x), indicates changes in the concavity of the function. A point of inflection occurs where f''(x) changes signs, which corresponds to a change in the direction of the slope of f'(x).
Outlines
🧮 Analyzing a Derivative Graph
This paragraph discusses solving an FRQ involving a differentiable function with given properties. The task involves finding specific function values by analyzing the graph of its derivative. Through integration and application of the fundamental theorem of calculus, the values of f(0) and f(5) are determined. Additionally, the points of inflection of the graph of f within a given interval are identified.
📉 Determining Decreasing Intervals
In this part, the focus is on understanding intervals where a derived function is decreasing. Through the analysis of g'(x) and the properties of f'(x), a number line is used to determine intervals where g(x) is decreasing. The process involves identifying critical points and assessing the behavior of g'(x) around these points to ascertain where g(x) is negative, indicating a decreasing function.
🔍 Finding the Absolute Minimum
The task here is to find the absolute minimum value of the function g(x) within a given interval. Utilizing a candidates test, which includes evaluating g at the interval endpoints and critical points, the absolute minimum value is determined. By computing g(0), g(5), and g(7), and comparing the values, the absolute minimum value within the interval is identified.
Mindmap
Keywords
💡Differentiable function
💡Interval
💡Derivative
💡Integral
💡Semicircle
💡Line segments
💡Fundamental Theorem of Calculus
💡Points of inflection
💡Second derivative
💡Function g
💡Absolute minimum value
Highlights
The function f is differentiable with f(4) = 3 on the interval [0, 7].
The graph of the derivative f' consists of a semicircle and two line segments.
Using the Fundamental Theorem of Calculus, f(4) - f(0) = integral from 0 to 4 of f'(t) dt.
The area under the curve from 0 to 4 is 3 + 2π, so f(0) = 3 + 2π.
To find f(5), integrate f'(t) dt from 4 to 5, which equals f(5) - f(4).
The area from 4 to 5 is a triangle with base 1 and height 1/2, so f(5) = 3 + 1/2 = 7/2.
Points of inflection occur where the second derivative f'' changes sign.
The slope of f' changes sign only at x = 6, so there is a point of inflection at x = 6.
Define g(x) = f(x) - x and find where g'(x) = f'(x) - 1 < 0 to determine where g is decreasing.
f'(x) = 0 at x = 5 and x = 7, which are the critical points to consider for g'(x).
g is decreasing on the interval [0, 5] since f'(x) < 1 between 0 and 5.
Evaluate g at endpoints 0, 5, and 7 to find the absolute minimum value of g on [0, 7].
g(0) = f(0) - 0 = 3 + 2π, g(7) = f(7) - 7 = -1/2, g(5) = f(5) - 5 = -3/2.
The absolute minimum value of g on [0, 7] is -1/2, which occurs at x = 7.
The area under the curve from 4 to 7 is a triangle plus a trapezoid, totaling 7/2.
f(7) is calculated by integrating from 4 to 7, resulting in f(7) = 13/2.
The minimum value of g occurs at x = 7, not at the endpoints 0 or 5.
The problem involves applying the Fundamental Theorem of Calculus and analyzing the behavior of the function and its derivatives.
The solution demonstrates the use of integration, critical points, and the concept of points of inflection in calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: