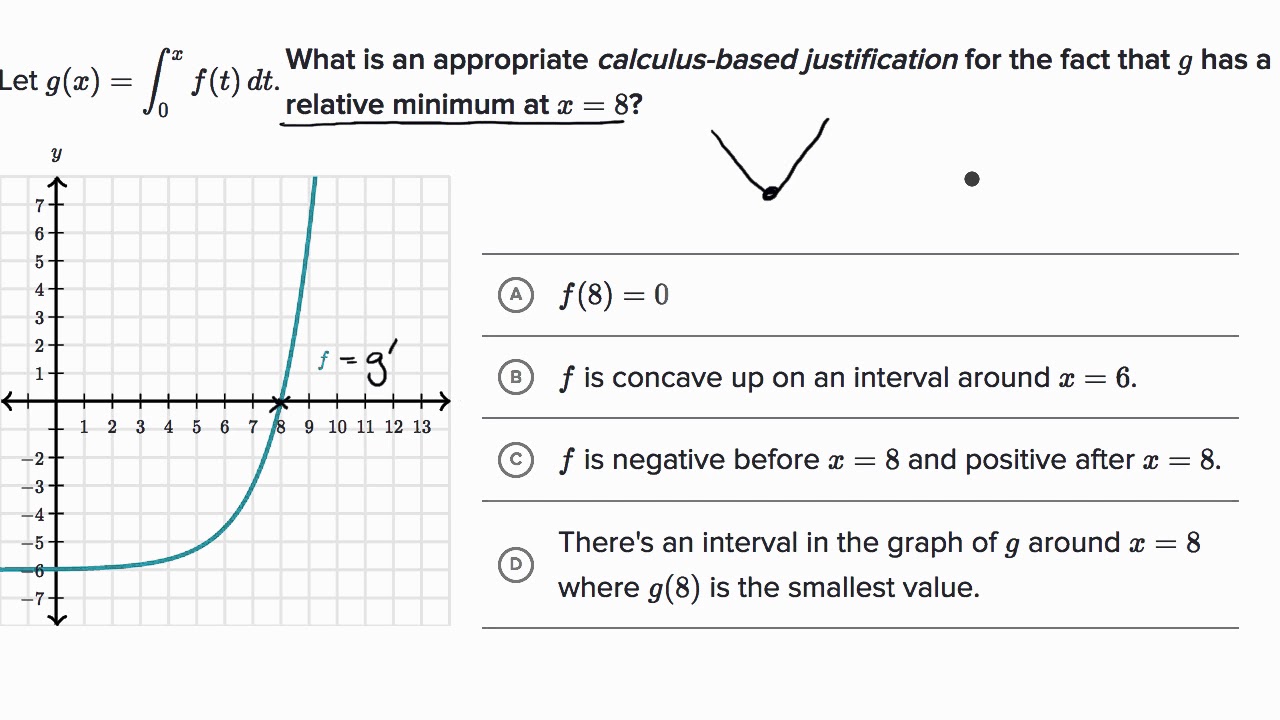
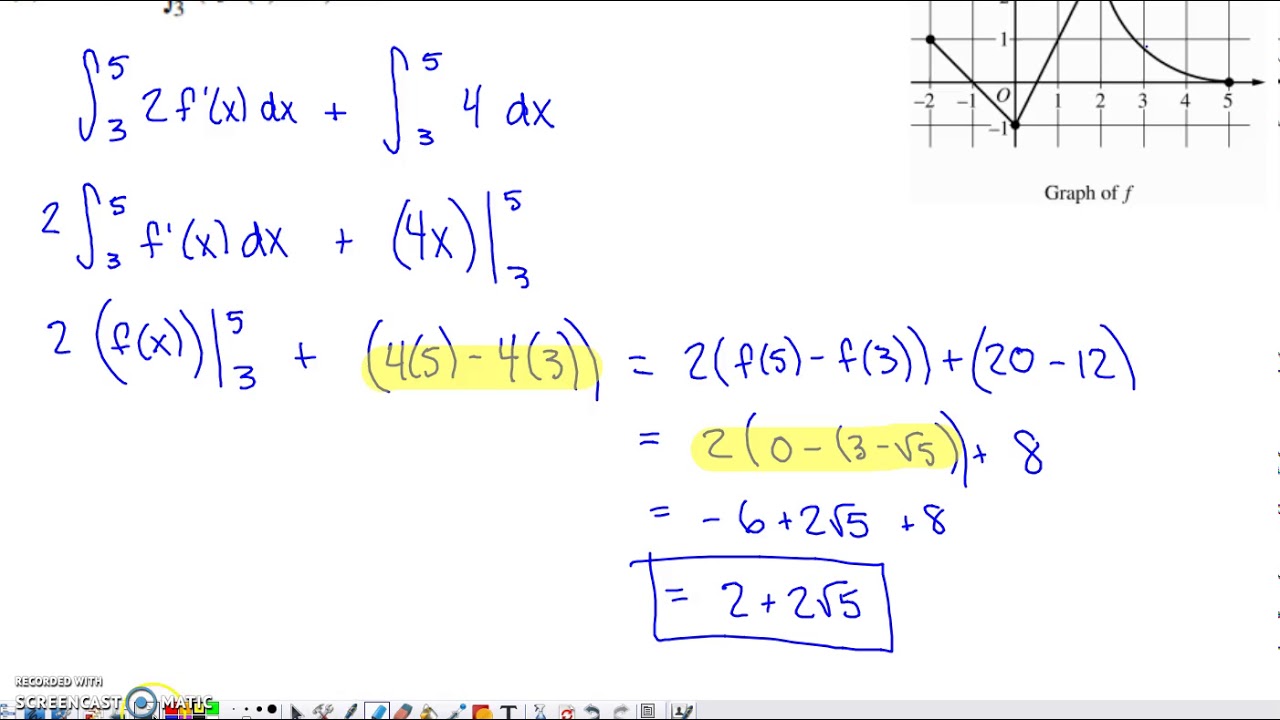
AP CALCULUS AB 2022 Exam Full Solution FRQ#3(c,d)
TLDRThe video script presents a detailed mathematical problem-solving session focused on the function g(x) defined as g(x) = f(x) - x. The presenter aims to identify intervals where g is decreasing within the range of 0 to 7. To do this, they calculate g'(x) as f'(x) - 1, using the given graph of f'(x). They find that g is decreasing between x = 0 and x = 5, as g'(x) is negative in this interval. In the second part, the presenter seeks to find the absolute minimum value of g on the interval 0 to 7. They use a candidates list, including critical points and endpoints, to compare the values of g at x = 0, x = 5, and x = 7. After calculating these values, they determine that the absolute minimum value of g is -1.5, which occurs at x = 5.
Takeaways
- 📌 The function g is defined as g(x) = f(x) - x, and we are interested in its decreasing intervals within 0 to 7.
- 📌 To determine where g is decreasing, we need to find g'(x), which is calculated as the derivative of f(x), and then subtract 1.
- 📌 The critical points for g are found by setting g'(x) to zero, resulting in f'(x) = 1, which occurs at x = 5 and x = 7.
- 📌 The slope of g at any point is determined by comparing f'(x) to 1; if f'(x) > 1, g'(x) is positive, and if f'(x) < 1, g'(x) is negative.
- 📌 By testing specific points, such as x = 4 and x = 6, we can confirm the slope and direction of g at those points.
- 📌 The interval where g is decreasing is from 0 to 5, as indicated by the negative slope in that region.
- 📌 To find the absolute minimum value of g on the interval 0 to 7, we consider critical points and endpoints.
- 📌 The endpoints are x = 0 and x = 7, and a critical point is found at x = 5, which is a local minimum.
- 📌 The values of g at the critical points and endpoints are calculated using the given function f and the definition of g.
- 📌 The absolute minimum value of g on the interval 0 to 7 is found by comparing the calculated y-values at x = 0, x = 5, and x = 7.
- 📌 The minimum value of g is determined to be at x = 5, with a y-value of -1.5.
- 📌 The process involves understanding the behavior of the derivative, calculating specific function values, and comparing these to find the minimum.
Q & A
What is the function g(x) defined as in the transcript?
-The function g(x) is defined as g(x) = f(x) - x.
What does it mean for g to be decreasing?
-For g to be decreasing, it means that the derivative of g, denoted as g'(x), is less than zero (g'(x) < 0).
How is g'(x) calculated in the transcript?
-g'(x) is calculated as the derivative of f(x), denoted as f'(x), and then subtracting 1 from it, so g'(x) = f'(x) - 1.
What is the interval where g(x) is decreasing?
-The interval where g(x) is decreasing is from 0 to 5.
What is the critical point in the interval 0 to 7?
-The critical point in the interval 0 to 7 is at x = 5, where f'(x) = 1.
How is the absolute minimum value of g(x) on the interval 0 to 7 found?
-The absolute minimum value is found by evaluating g(x) at the critical points and endpoints within the interval, which are x = 0, x = 5, and x = 7.
What is the value of g(0)?
-The value of g(0) is calculated as g(0) = f(0) - 0, which is 3 + 2π.
What is the value of g(5)?
-The value of g(5) is calculated as g(5) = f(5) - 5, which results in -1.5.
What is the value of g(7)?
-The value of g(7) is calculated as g(7) = f(7) - 7, which results in -0.5.
What is the absolute minimum value of g(x) on the interval 0 to 7?
-The absolute minimum value of g(x) on the interval 0 to 7 is y = -1.5, which occurs at x = 5.
How are the areas under the f'(x) graph calculated?
-The areas under the f'(x) graph are calculated by breaking them up into triangles and trapezoids, and then summing their respective areas.
What is the method used to find the absolute minimum value of g(x)?
-The method used to find the absolute minimum value of g(x) is by creating a candidate list of critical points and endpoints and then comparing their g(x) values to determine the minimum.
Outlines
📉 Finding Intervals of Decrease for Function g
The video begins by addressing question three c, focusing on the function g(x) defined as g(x) = f(x) - x. The goal is to determine the intervals where g is decreasing within the range from 0 to 7. To do this, the derivative of g, denoted as g'(x), is calculated, which is found to be g'(x) = f'(x) - 1. With the graph of f'(x) provided, the video identifies the points where g'(x) equals zero, which are at x = 5 and x = 7. By analyzing the slope of g'(x), it's determined that g is decreasing in the interval from 0 to 5. The video then moves on to part d, where it seeks to find the absolute minimum value of g on the interval 0 to 7. To justify this, a list of candidates is compiled, including critical points and endpoints. The local minimum at x = 5 is identified as a candidate, and the values of g at x = 0, x = 5, and x = 7 are calculated using the given function f. The minimum value is found to be at g(5), which is -1.5.
🔍 Calculating the Absolute Minimum Value of g
The second paragraph delves into calculating the absolute minimum value of the function g on the interval from 0 to 7. The video uses a candidates list approach, which includes endpoints at x = 0 and x = 7, as well as the critical point at x = 5. To evaluate g at these points, the values of f(x) at x = 0, x = 5, and x = 7 are required. The video calculates f(0) as 3 + 2π, f(5) as 3.5, and determines f(7) by finding the area under the curve of f'(x) from x = 4 to x = 7, which is a combination of a triangle and a trapezoid, resulting in f(7) = 6.5. Consequently, g(7) is calculated as f(7) - 7, which equals -0.5. After evaluating g at all candidates, it is concluded that the absolute minimum value of g is -1.5, which occurs at x = 5.
Mindmap
Keywords
💡Function g
💡Decreasing function
💡Derivative
💡Critical points
💡Endpoints
💡Absolute minimum value
💡Slope chart
💡Area under the curve
💡Candidates list
💡F prime graph
💡Local minimum
💡Interval
Highlights
The function g(x) is defined as g(x) = f(x) - x.
To determine where g is decreasing, we need to find g'(x).
Differentiating g with respect to x gives g'(x) = f'(x) - 1.
The graph of f'(x) is provided to assist in finding g'(x).
Setting g'(x) to zero to find critical points results in f'(x) = 1.
f'(x) equals 1 at x = 5 and x = 7.
The slope of g at x = 4 is negative, indicating a decreasing interval.
At x = 6, g'(x) is positive, indicating an increasing interval.
The interval [0, 5] is identified as where g is decreasing.
To find the absolute minimum value of g on [0, 7], consider critical points and endpoints.
Endpoints are at x = 0 and x = 7, and a critical point at x = 5.
The y-values for the candidates are calculated using known f(x) values.
g(0) is calculated to be 3 + 2π using the given f(0).
g(5) is found to be -1.5, which is the lowest point so far.
To find g(7), the area under the curve from x = 4 to x = 7 is calculated.
f(7) is determined by adding the area under the f'(x) graph from 4 to 7 to the starting coordinate of 3.
The area from x = 4 to x = 7 is a combination of a triangle and a trapezoid, totaling 3.5.
f(7) is calculated to be 6.5, and subsequently g(7) is found to be -0.5.
Comparing the candidate y-values, g(5) is identified as the absolute minimum value at -1.5.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: