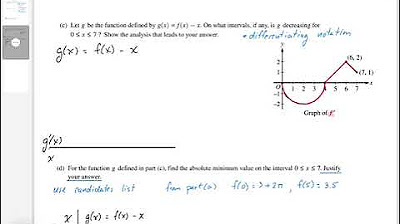2022 AP Calculus AB & AP Calculus BC Exam FRQ #3
TLDRThe video script discusses a calculus problem from the 2022 AP Calculus AB and BC exams, which involves analyzing a given graph of a derivative function. The problem requires finding the values of the function at specific points, identifying points of inflection, and determining intervals of decrease for a related function. The presenter uses the Fundamental Theorem of Calculus to find f(0) and f(5), explains how to identify points of inflection by looking for changes in the concavity of the derivative, and analyzes the function g(x) = f(x) - x to find its decreasing interval and absolute minimum value on the interval [0, 7]. The summary provides a clear and concise overview of the problem-solving process, making it accessible to users interested in calculus.
Takeaways
- 📈 The problem involves a differentiable function f with a given graph of its derivative, f', consisting of a semicircle and two line segments.
- 🧮 To find f(0), one should integrate f' from 0 to 4 and subtract the result from the known value f(4), which is 3.
- 🔍 The area of the semicircle with radius 2 is πr²/2, which is 2π, and since it's below the x-axis, it contributes negatively to the integral.
- 📐 The function f(0) is calculated to be 3 + 2π after accounting for the area under the semicircle.
- 🚀 For f(5), integrate f' from 4 to 5 and add it to f(4), which involves a half-square with an area of 1/2.
- 📦 The value of f(5) is determined to be 3 + 1/2, or 7/2.
- 🤔 Points of inflection for the function f occur where f' changes from increasing to decreasing or vice versa, specifically at x = 2 and x = 6.
- 📉 The function g(x) = f(x) - x is decreasing on the interval [0, 5] because g'(x) = f'(x) - 1 is less than zero in that region.
- ⛰️ The absolute minimum value of g(x) on the interval [0, 7] occurs at x = 5, and it is -1.5, found by evaluating g at the endpoints and critical points.
- 🔢 The candidate's test is used to determine that the absolute minimum of a continuous function like g occurs at endpoints or critical points.
- 📋 The analysis involves creating a table with values of x, g(x), and comparing them to find the absolute minimum value.
Q & A
What is the main topic of the video?
-The video discusses problem number three from the 2022 Calculus AB and BC exams, which involves a differentiable function and its derivative graph.
What is the first task the video sets out to accomplish?
-The first task is to find the values of the function f at x = 0 and x = 5 using the Fundamental Theorem of Calculus.
What is the value of f(0) according to the video?
-The value of f(0) is 3 + 2π, as calculated by subtracting the area under the graph of the derivative (which is -2π) from the known value f(4) = 3.
How is the value of f(5) determined in the video?
-The value of f(5) is determined by adding the displacement from 4 to 5, which is the definite integral from 4 to 5 of f'(x) dx, to the known value f(4) = 3, resulting in f(5) = 3.5.
What does the video say about the x-coordinates of the points of inflection for the graph of f on the interval [0, 7]?
-The video identifies the x-coordinates of the points of inflection as x = 2 and x = 6, justified by the fact that f'(x) has relative extrema at these points.
What is the function g(x) defined as in the video?
-The function g(x) is defined as g(x) = f(x) - x.
On which interval is the function g(x) determined to be decreasing?
-The function g(x) is determined to be decreasing on the interval from 0 to 5, as g'(x) < 0 on that interval.
How does the video justify that g(x) is decreasing on the interval [0, 5]?
-The video justifies that g(x) is decreasing on the interval [0, 5] by showing that g'(x) < 0, which implies f'(x) < 1, and identifying the region where f'(x) is less than 1.
What is the method used in the video to find the absolute minimum value of g(x) on the interval [0, 7]?
-The video uses the candidate's test, which involves finding the values of g(x) at endpoints and critical points, and then determining where the function has the lowest value.
At which x-coordinate does the video find the absolute minimum value of g(x)?
-The absolute minimum value of g(x) is found at x = 5, with a value of -1.5.
What is the significance of the semicircle in the derivative graph for the function f?
-The semicircle in the derivative graph represents the area under the curve of f'(x) from x = 0 to x = 2, which contributes to the calculation of f(0) using the Fundamental Theorem of Calculus.
How does the video handle the calculation of f(7)?
-The video calculates f(7) by adding the integral of f'(x) from x = 4 to x = 7 to the known value f(4) = 3, and then subtracting the x-coordinate (7), resulting in a value of -0.5 for f(7) - x at x = 7.
Outlines
📈 Calculus Problem: Derivative Graph Analysis
This paragraph introduces a calculus problem from the 2022 AP Calculus AB and BC exams, which involves analyzing a graph of a derivative function, f'(x). The function f is differentiable with f(4) = 3 on the interval [0, 7]. The graph of f' consists of a semicircle and two line segments. The task is to find f(0) and f(5) using the Fundamental Theorem of Calculus. The presenter calculates f(0) by subtracting the integral from 0 to 4 (which involves the area of a semicircle) from f(4), resulting in f(0) = 3 + 2π. To find f(5), the presenter adds the integral from 4 to 5 to f(4), considering the area of a half-square, to get f(5) = 3 + 1/2. The presenter also discusses finding points of inflection by looking for where f' changes from increasing to decreasing or vice versa, identifying x = 2 and x = 6 as such points due to relative extrema.
📉 Function g Analysis: Decreasing Intervals and Absolute Minimum
The second paragraph deals with the function g(x) = f(x) - x, where f is the function from the previous discussion. The goal is to determine the intervals where g is decreasing on the interval [0, 7]. The presenter finds the derivative of g, g'(x) = f'(x) - 1, and looks for where g' is less than zero, which corresponds to where f' is less than 1. By analyzing the graph, the presenter identifies the interval [0, 5] as where g is decreasing. The reasoning is that g' is less than 0 on this interval, indicating that f' is less than 1. Furthermore, the presenter seeks to find the absolute minimum value of g on [0, 7]. Since g is continuous, the absolute minimum will occur at an endpoint or a critical point. The critical points are identified as x = 5 and x = 7, where f' equals 1, making g' zero. The presenter uses the Candidate's Test to evaluate the endpoints and critical points, calculating the values of g at x = 0, x = 5, and x = 7. After computation, it is determined that the absolute minimum value of g is -1.5 at x = 5.
Mindmap
Keywords
💡Derivative
💡Fundamental Theorem of Calculus
💡Integral
💡Semicircle
💡Line Segments
💡Area Problem
💡Point of Inflection
💡Relative Extrema
💡Decreasing Function
💡Critical Points
💡Absolute Minimum
💡Candidate's Test
Highlights
The video discusses problem number three from the 2022 Calculus AB and BC exams, which involves analyzing a graph of a derivative.
A differentiable function f is given with f(4) = 3 on the interval [0, 7].
The graph of f' (the derivative of f) consists of a semicircle and two line segments.
The Fundamental Theorem of Calculus is applied to find f(0) and f(5).
f(0) is calculated by subtracting the integral from 0 to 4 of f' from f(4).
The area of the semicircle with radius 2 is used to find f(0), which results in f(0) = 3 + 2π.
For finding f(5), the integral from 4 to 5 of f' is added to f(4), resulting in f(5) = 3 + 1/2.
Points of inflection for the graph of f are identified at x = 2 and x = 6 based on changes in the monotonicity of f'.
A justification using relative extrema of f' is preferred to identify points of inflection.
The function g(x) = f(x) - x is defined, and its intervals of decrease are analyzed between 0 and 7.
g'(x) = f'(x) - 1 is used to determine when g(x) is decreasing, which is when f'(x) < 1.
The interval [0, 5] is identified as where g(x) is decreasing, as g' is less than 0 in this interval.
The absolute minimum value of g(x) on the interval [0, 7] is sought, considering endpoints and critical points.
The Candidate's Test is mentioned for finding the absolute minimum of a continuous function.
Critical points for g(x) are found where g'(x) = 0, which are at x = 5 and x = 7.
Values of g(x) at endpoints and critical points are calculated to determine the absolute minimum.
The absolute minimum of g(x) is found to be -1.5 at x = 5.
The video concludes with a summary of the problem-solving process, emphasizing the importance of showing work as if taking the AP exam.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: