2011 Calculus AB free response #4c | AP Calculus AB | Khan Academy
TLDRThe video script discusses the concept of a point of inflection on a graph, which occurs where the sign of the second derivative changes. It explains this with the help of a graphical example and then applies the concept to a specific function, g(x), which is defined as an integral. The script details the process of finding the first and second derivatives of g(x) and emphasizes that a sign change in the first derivative of the integrand (f(x)) corresponds to a point of inflection in g(x). Despite f(x) being non-differentiable at a certain point, a sign change in its slope indicates a point of inflection for g(x) at x=0.
Takeaways
- 📈 An inflection point on a graph is characterized by a change in the sign of the second derivative.
- 🔄 The second derivative must transition from positive to negative or vice versa at an inflection point.
- 🌐 Visually, an inflection point can be imagined as a curve where the slope moves from negative to positive or increasing to decreasing.
- 📌 The process of identifying inflection points involves finding where the second derivative changes sign.
- 👁️🗨️ The function g(x) is given as an integral, and its first derivative, g'(x), is influenced by the function f(x).
- 🔢 For g(x), the second derivative, g''(x), is the derivative of f(x), leading to the conclusion that the sign change in f'(x) corresponds to an inflection point in g(x).
- 🌟 The slope of f(x) represents the instantaneous rate of change, which is crucial for identifying sign changes.
- 📊 The script describes a scenario where the slope of f(x) is positive throughout a certain interval, then experiences a sign change at x=0, indicating an inflection point for g(x).
- ⚠️ Even if f(x) is not differentiable at a certain point, a sign change in the slope can still indicate an inflection point.
- 📍 The specific example in the script concludes that at x=0, g(x) has a point of inflection due to the observed sign change in the first derivative of f(x).
Q & A
What is the main topic of the transcript?
-The main topic of the transcript is the concept of a point of inflection on a graph and how to identify it by examining the behavior of the second derivative of a function.
What is a point of inflection?
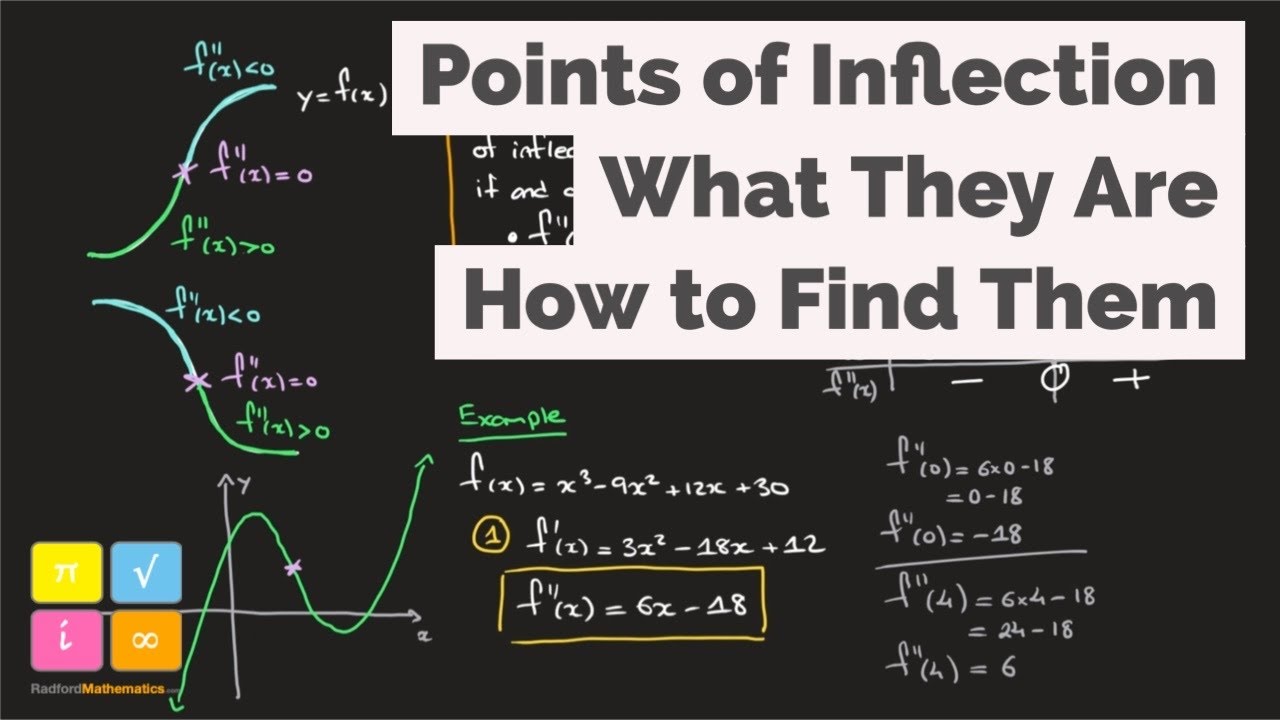
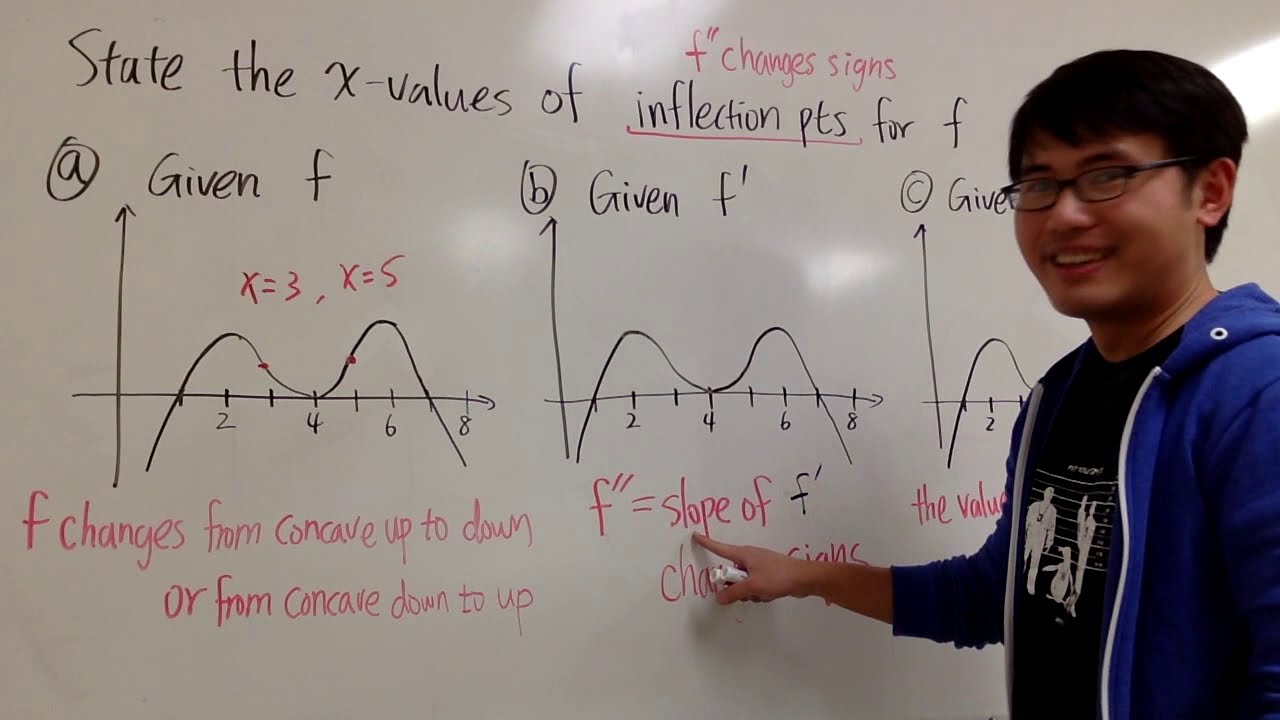
-A point of inflection is a point on the graph of a function where the concavity of the graph changes. This means the sign of the second derivative changes, indicating a change from concave up to concave down or vice versa.
How does the sign of the second derivative indicate a point of inflection?
-The sign of the second derivative indicates a point of inflection because if it changes from positive to negative, the graph goes from curving upwards to curving downwards, or if it changes from negative to positive, the graph goes from curving downwards to curving upwards.
What is the function g(x) mentioned in the transcript?
-The function g(x) mentioned in the transcript is g(x) = 2x + the definite integral from 0 to x of f(t) dt. It is a combination of a linear term and a term resulting from the integral of another function, f(t).
How is the first derivative of g(x) calculated?
-The first derivative of g(x), denoted as g'(x), is calculated using the fundamental theorem of calculus. The derivative of the integral term is f(x), so g'(x) = 2 + f(x).
What is the second derivative of g(x) and how is it related to the point of inflection?
-The second derivative of g(x), denoted as g''(x), is the derivative of g'(x). It is equal to the derivative of f(x), which is f'(x). The point of inflection is identified where g''(x) has a sign change, indicating a change in the slope or concavity of the graph of g(x).
What is the significance of the slope of f(t) in relation to the point of inflection for g(x)?
-The slope of f(t) is significant because the first derivative of f(t) corresponds to the second derivative of g(x). A sign change in the slope of f(t) indicates a point of inflection for g(x), as it corresponds to a change in the concavity of the graph of g(x).
How does the transcript describe the visual identification of a point of inflection?
-The transcript describes the visual identification of a point of inflection by discussing the behavior of the slope of the function. It explains that the slope changes from positive to negative or vice versa, and this change can be visually observed as the curve transitions from increasing to decreasing or vice versa.
What is the example of a point of inflection given in the transcript?
-The example of a point of inflection given in the transcript occurs at x = 0. Despite f not being differentiable at this point, there is a sign change in the slope from positive to negative, indicating a point of inflection for the graph of g(x).
How does the concept of a point of inflection relate to real-world applications?
-While the transcript does not explicitly mention real-world applications, the concept of a point of inflection can be relevant in various fields such as physics, where it can describe changes in acceleration, or in economics, where it can indicate changes in the rate of profit or loss over time.
What is the conclusion drawn from the analysis in the transcript?
-The conclusion drawn from the analysis in the transcript is that at x = 0, there is a sign change in the first derivative of f(t), which corresponds to a sign change in the second derivative of g(x). This indicates that the graph of g(x) has a point of inflection at x = 0.
Outlines
📚 Understanding Inflection Points
This paragraph discusses the concept of inflection points on a graph, which are points where the sign of the second derivative changes. It explains that an inflection point is characterized by a change from positive to negative or vice versa in the slope of the function. The explanation includes visual examples and transitions to discussing the specific function g(x), which is defined as an integral. The process of finding the second derivative of g(x) is outlined, and the significance of the first derivative of f(x) in determining the inflection point is highlighted. The paragraph concludes by identifying a sign change in the first derivative of f(x) at x=0, indicating a point of inflection for g(x).
Mindmap
Keywords
💡Interval
💡Point of Inflection
💡Second Derivative
💡Sign Change
💡Slope
💡Definite Integral
💡Fundamental Theorem of Calculus
💡Differentiable
💡Instantaneous Slope
💡Concavity
💡Discontinuity
Highlights
The main objective is to find values of x where the graph of g(x) has a point of inflection within the interval (-4, 3).
An inflection point is characterized by a change in the sign of the second derivative.
The second derivative's sign change can be visualized as the slope transitioning from positive to negative or vice versa.
The concept of inflection points can be better understood by considering the slope or instantaneous slope of a function.
The function g(x) is defined as an integral, and its derivative is utilized to find points of inflection.
The first derivative of g(x), g'(x), is calculated using the fundamental theorem of calculus.
The second derivative of g(x), g''(x), is found by differentiating g'(x), which leads to the analysis of f'(x).
The sign change in the first derivative of f(x) corresponds to a sign change in the second derivative of g(x).
The analysis of the slope of f(x) reveals a sign change at x = 0, indicating a point of inflection for g(x).
Even though f(x) is not differentiable at a certain point, a sign change in the slope can still indicate a point of inflection.
The slope of f(x) transitions from positive to negative at x = 0, signifying a point of inflection for the graph of g(x).
The function g(x) is challenging to visualize, so focusing on the second derivative's sign change is crucial for finding points of inflection.
The process of finding points of inflection involves understanding the behavior of a function's derivatives and their corresponding slopes.
The concept of inflection points is essential in calculus as it helps in understanding the function's behavior and its graphical representation.
The analysis of g(x)'s second derivative provides a comprehensive understanding of the function's behavior within the given interval.
The method of identifying points of inflection can be applied to various types of functions, including those involving integrals and their derivatives.
The practical application of finding points of inflection can be useful in various mathematical and real-world scenarios, such as optimization problems and modeling.
The discussion on points of inflection emphasizes the importance of understanding the behavior of a function beyond just its critical points.
Transcripts
Browse More Related Video

Mistakes when finding inflection points: second derivative undefined | AP Calculus AB | Khan Academy

Worked example: Inflection points from first derivative | AP Calculus AB | Khan Academy

2022 AP Calculus AB BC Free Response #3

Inflection points (algebraic) | AP Calculus AB | Khan Academy
Point of Inflection - Point of Inflexion - f''(x)=0 - Definition - How to Find - Worked Example 1
Points of inflection from the graphs of f, f' or f''
5.0 / 5 (0 votes)
Thanks for rating: