Math 11 - Section 2.2
TLDRIn this educational video, Professor Monty dives into Section 2.2, focusing on the calculus of exponential and logarithmic functions. He explains that the derivative of e^x, where e is the base of the natural logarithm, is unique as it equals the original function. This is demonstrated through graphical representation and the concept of the derivative as the slope of the tangent line. The video continues with an exploration of the chain rule in the context of exponential functions, showing how the derivative of e^(some function) involves multiplying e^(function) by the derivative of that function. Several examples illustrate the process of differentiating exponential functions, highlighting the distinction between exponential and power functions. The video concludes with applications of these concepts, such as modeling the growth of a retirement fund and memory retention, emphasizing the practical relevance of understanding calculus in real-world scenarios.
Takeaways
- 📈 The derivative of the exponential function e^x is unique in that it is the same as the original function, e^x.
- 🔗 The chain rule is applied when differentiating exponential functions with a variable exponent, resulting in e^u * du/dx, where u is the exponent.
- 📚 When differentiating exponential functions, remember that the base e is the only base whose derivative is the function itself.
- ⛰ The graph of y = e^x has a special property where the slope of the tangent line at any point (x, e^x) is equal to the value of the function at that point.
- 📖 In the context of word problems, exponential functions can model continuous growth or decay, such as in the case of a retirement fund or memory retention.
- 🧮 The formula for continuous compound interest is used to calculate the future value of an investment, which involves exponential functions.
- 📉 For exponential decay, the rate of forgetting information can be modeled by an exponential function, where the rate of decay is given by the derivative of the function.
- 🔢 The limit of an exponential decay function as time goes to infinity can be found by understanding the behavior of the denominator as it grows larger.
- 📌 The quotient rule and product rule are essential for differentiating more complex functions involving exponential terms, especially when they are multiplied or divided by other functions.
- 📐 The graph of an exponential decay function will have a horizontal asymptote, showing the long-term limit of the function's value.
- 🤔 Understanding the meaning of the derivative in applied problems, such as predicting the next year's interest on an investment or the number of words a student will remember, is crucial for interpreting the results correctly.
Q & A
What is the main topic of discussion in section 2.2 of the video?
-The main topic of discussion in section 2.2 is the calculus aspect of exponential and logarithmic functions.
What is special about the exponential function e^x?
-The special property of the exponential function e^x is that its derivative is the same as the original function itself.
What is the chain rule in calculus?
-The chain rule in calculus is used to compute the derivative of composite functions. It states that the derivative of a function composed of two functions is the derivative of the outer function evaluated at the inner function, times the derivative of the inner function.
How does the derivative of e^(3x) compare to e^x?
-The derivative of e^(3x) is 3e^(3x), which is different from e^x because of the application of the chain rule, where the derivative of the inner function (3x) is multiplied by the derivative of e^x.
What is the difference between the derivative of a power function and an exponential function?
-The derivative of a power function, such as x^n, decreases the exponent by 1, resulting in n*x^(n-1). In contrast, the derivative of an exponential function e^x remains e^x, as the exponent does not decrease.
What is the formula for continuous compound interest?
-The formula for continuous compound interest is A = P * e^(rt), where A is the amount of money accumulated after n years, including interest, P is the principal amount (the initial amount of money), r is the annual interest rate (in decimal), t is the time the money is invested for in years, and e is the base of the natural logarithm.
How is the rate of change of the value of an IRA account calculated?
-The rate of change, or the derivative, of the value of an IRA account is calculated by differentiating the continuous compound interest formula with respect to time. This derivative represents the predicted interest for the next year based on the current amount in the account.
What is the limit of the number of words a student remembers as the number of days goes to infinity?
-As the number of days goes to infinity, the limit of the number of words a student remembers approaches a constant value, which in the given model is 35 words. This suggests that the student will always remember 35 words regardless of the time passed.
How does the quotient rule apply to the function G(x) = (x^6) / (e^(3x))?
-The quotient rule is applied to find the derivative of G(x) by taking the derivative of the numerator and the denominator separately and then using the formula: G'(x) = (e^(3x) * 6x^5 - x^6 * 3e^(3x)) / (e^(3x))^2.
What does the second derivative of a function represent?
-The second derivative of a function represents the rate of change of the rate of change, or the curvature of the function. A positive second derivative indicates that the function is concave up, while a negative second derivative indicates that the function is concave down.
How does the concept of exponential decay apply to the memory retention problem?
-The concept of exponential decay is used to model the decrease in the number of words a student remembers over time. The formula provided for the number of words retained W after T days is an exponential decay function, which shows that the number of words remembered decreases at a rate proportional to the number of words currently remembered.
Outlines
📚 Introduction to Calculus of Exponential Functions
Professor Monty begins by reviewing the algebra of exponential and logarithmic functions from the previous video. He then introduces the calculus aspect, focusing on the unique property of the exponential function e^x, where the derivative is the same as the original function. The chain rule is also discussed in the context of exponential functions, and several examples are provided to illustrate the process of differentiation.
🔢 Applying the Chain Rule to Exponential Functions
The second paragraph delves into applying the chain rule to exponential functions. It covers how to differentiate composite exponential functions, such as e^(3x) and 2e^(4x), by multiplying the base exponential function with the derivative of the exponent. The paragraph also contrasts exponential functions with power functions and demonstrates the differentiation of a function that is a combination of both, using both the power rule and the chain rule.
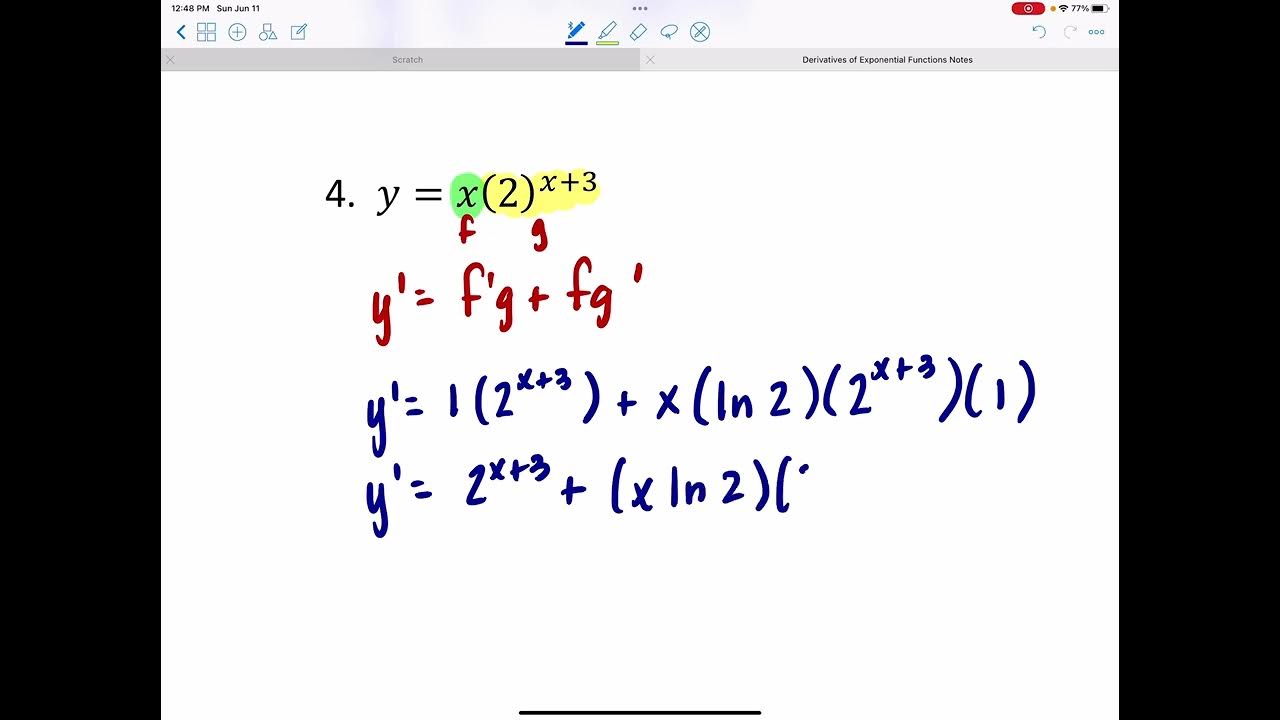
📈 Product and Quotient Rules in Differentiation
The third paragraph discusses the application of the product and quotient rules in differentiation. It explains the product rule formula and illustrates its use with an example involving the function x^7 * e^(4x). The quotient rule is also introduced, and an example is provided to show how to differentiate a quotient of exponential and polynomial functions. The importance of factoring out common terms in the derivative is highlighted.
💹 Word Problems: Retirement Fund Growth
In the fourth paragraph, Professor Monty presents a word problem involving the growth of a retirement fund. The problem uses the formula for continuous compound interest to model the value of an IRA account over time. The derivative of the function is used to estimate the rate of change in the account's value at the end of seven years, demonstrating how derivatives can be applied to real-world scenarios.
📉 Memory Retention Model and Its Limit
The fifth paragraph explores a model for memory retention, where a student's ability to recall vocabulary words diminishes over time. The model is represented by an exponential decay function, and the paragraph discusses how to find the number of words retained after specific time intervals. It also addresses the limit of the number of words the student will remember as time goes to infinity, which is a constant number based on the model.
📊 Graphing the Memory Retention Function
The sixth paragraph involves graphing the memory retention function to visualize how the number of retained words decreases over time. The graph is shown to have a horizontal asymptote at 35 words, indicating that the student will eventually stabilize at remembering 35 words indefinitely. The paragraph also discusses the concavity of the graph, which is determined by the sign of the first and second derivatives.
🔁 Rate of Forgetting and Derivatives
The final paragraph focuses on calculating specific values of the memory retention function and its derivative at a given time (7 days). It shows how to find the number of words retained after seven days and the rate of forgetting, which is the derivative of the retention function. The paragraph emphasizes the interpretation of the derivative in the context of the problem, indicating the number of words forgotten per day.
Mindmap
Keywords
💡Exponential Functions
💡Derivative
💡Chain Rule
💡Continuous Compound Interest
💡Logarithmic Functions
💡Tangent Line
💡Product Rule
💡Quotient Rule
💡Memory Retention
💡Limit
💡Graphing
Highlights
Professor Monty begins a lecture on calculus aspects of exponential and logarithmic functions.
The special property of the exponential function e^x is that its derivative is the same as the original function.
The chain rule is introduced for derivatives of exponential functions involving composed functions.
The derivative of e^x is e^x, which is unique among functions except for the zero function.
Examples are provided to illustrate the differentiation of exponential functions using the chain rule.
The difference between exponential and power functions in terms of their derivatives is explained.
The product rule is applied to the function x^7 * e^(4x), demonstrating its use in calculus.
The quotient rule is discussed in the context of the function (e^(3x) / (x^6)) and its derivative.
A word problem involving the growth of a retirement fund illustrates the application of exponential functions in real-world scenarios.
The rate of change in the value of an IRA account is calculated using the derivative of the growth model.
The limit of the number of words a student remembers is explored as time goes to infinity, using exponential decay.
The concept of continuous compound interest is explained using the formula for an IRA account's growth.
The use of a graphing calculator to visualize the retention of vocabulary words over time is demonstrated.
The derivative of the memory retention function is calculated to find the rate at which words are forgotten.
The importance of the chain rule in differentiating exponential functions is emphasized.
Practical applications of exponential functions are discussed, highlighting their relevance in modeling growth and decay.
Homework and practice problems are encouraged to solidify understanding of the calculus of exponential functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: