Business Calculus - Math 1329 - Section 1.4 - Functional Models
TLDRThe video script discusses the application of mathematical functions to solve real-world problems. It begins with a scenario where a farmer wants to build a rectangular pen for horses using 600 feet of fencing, and the script guides through finding the dimensions that maximize the pen's area, resulting in a square pen. The second example involves a similar problem but with a barn, leading to different dimensions. The third example is about designing an open-top box with minimum material cost, which involves creating a cost function and using a graphing calculator to find the dimensions that minimize cost. The final section delves into market equilibrium, explaining how supply and demand functions intersect to determine the equilibrium price and quantity. The script includes an example of market research for two-liter sodas, illustrating how to calculate the market equilibrium and price per soda.
Takeaways
- 📐 **Functional Models**: The concept of transforming word problems into functions to analyze and solve geometric and real-world problems.
- 🏁 **Problem-Solving Approach**: Breaking down problems, identifying key variables, and using geometric or algebraic methods to find solutions.
- 🔍 **Perimeter and Area**: Using the perimeter of a rectangle to find its dimensions and the largest possible area it can enclose with a given amount of fencing.
- 📏 **Optimizing Rectangles**: Demonstrating that a square (a special type of rectangle) provides the maximum area for a given perimeter.
- 📈 **Quadratic Functions**: Applying the vertex formula to find the maximum or minimum values of quadratic functions, which is crucial in optimization problems.
- 🧱 **Cost Minimization**: Finding the dimensions of a box that minimize the total cost of materials, considering different costs for lateral sides and the base.
- 📊 **Graphing Calculators**: Utilizing graphing calculators to find minimum or maximum values of functions, especially when they are not easily solvable algebraically.
- ⚖️ **Market Equilibrium**: Understanding the balance between supply and demand and how it affects the price and quantity of goods in a market.
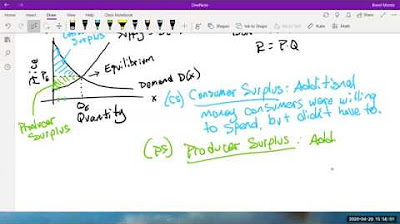
- 📉 **Surplus and Shortage**: Recognizing the economic consequences of producing more (surplus) or less (shortage) than what is demanded at a given price.
- 💰 **Equilibrium Price and Quantity**: Calculating the price and quantity at which supply equals demand, which is key to achieving market equilibrium.
- 📋 **Real-World Application**: Applying mathematical models to real-world scenarios, such as determining the optimal production levels for market equilibrium in the soda industry.
Q & A
What is the primary goal when creating functional models from word problem scenarios?
-The primary goal is to translate the aspects of the word problem into a function, which can then be used to perform various calculations, such as finding the largest or smallest value of the function.
In the context of the farmer's rectangular pin problem, what does 'largest possible pin' refer to?
-It refers to the pin with the largest possible area, which is the amount of space enclosed by the fence.
How does the perimeter of a rectangle relate to the fencing problem in the farmer's scenario?
-The 600 feet of fencing available is equivalent to the perimeter of the rectangular pin, which is calculated as 2x + 2y for a rectangle with sides of length x and y.
What is the formula used to find the area of a rectangle?
-The area of a rectangle is found by multiplying its length by its width, which is expressed as A = x * y.
How does solving the perimeter equation for y help in the farmer's pin problem?
-Solving the perimeter equation for y reduces the problem to a single variable (x), which simplifies the process of finding the dimensions that maximize the area of the rectangle.
What technique is used to find the maximum area of a quadratic function?
-The vertex formula, which is x = -b / (2a), is used to find the maximum area of a quadratic function.
What is the relationship between the dimensions of the largest pin and the shape of the rectangle?
-The largest pin is a square with dimensions 150 feet by 150 feet, as it turns out that a square provides the maximum area for a given perimeter.
In the second example, how does the farmer's decision to build the pin against the barn affect the fencing required?
-Building the pin against the barn means only three sides of the pin require fencing, resulting in a perimeter equation of 2x + y = 600, as opposed to the four-sided 600 feet perimeter in the first example.
What is the volume of the open-top rectangular box in the third example, and how does it affect the cost function?
-The volume of the open-top rectangular box is 6,000 cubic feet. This volume, along with the costs of materials for the lateral sides and base, affects the cost function, which is used to determine the dimensions that minimize the total cost of building the box.
How is the cost function simplified when finding the minimum cost for the open-top box?
-The cost function is simplified by substituting the expression for H (height) derived from the volume equation into the cost function, resulting in a single-variable function in terms of X (length).
What is the concept of market equilibrium, and how does it relate to supply and demand?
-Market equilibrium is the point where the quantity demanded by consumers is equal to the quantity supplied by producers at a given price. It is the balance point where neither a surplus nor a shortage exists.
How are the supply and demand functions used to find the market equilibrium for the two-liter sodas?
-The supply and demand functions are set equal to each other to find the market equilibrium. By solving for X (the number of thousands of units), the quantity that should be produced and sold to achieve market equilibrium is determined.
Outlines
📐 Creating Functional Models for Problem Solving
This paragraph introduces the concept of creating functional models from word problem scenarios. The focus is on transforming a problem into a function to find various values such as the maximum or minimum of the function. An example of a farmer building a rectangular pen with a limited amount of fencing material is used to illustrate the process. The problem is broken down into geometric terms, and the relationship between the perimeter of the rectangle (600 feet) and the area it encloses is explored. The solution involves creating a function for the area in terms of one variable (X), which is then used to find the dimensions and area that maximize the pen's size.
🔍 Maximizing Rectangle Area with Limited Resources
The second paragraph continues the theme of optimizing rectangles but introduces a variation where the farmer builds a pen against a barn, requiring fencing for only three sides. The perimeter equation is adjusted accordingly (2x + y = 600), and the area function is manipulated to express y in terms of x. Using the vertex formula for a quadratic function, the maximum area is found, leading to the conclusion that a square provides the largest area. The dimensions and the largest possible area for the pen are calculated based on the given constraints.
📦 Minimizing Cost for an Open-Top Box Design
The third paragraph shifts the focus to designing an open-top rectangular box with a fixed volume and specific width to minimize construction cost. The cost function includes the cost of material for the lateral sides and the base, with different costs per square foot. Using the volume constraint and the cost function, an equation relating the dimensions of the box to the cost is formulated. The minimum cost is found by graphing the function and using a graphing calculator to determine the dimensions that yield the minimum cost. The resulting box dimensions and the minimum cost are provided.
📈 Solving for Market Equilibrium in Soda Production
The fourth paragraph discusses the concept of market equilibrium using the example of two-liter soda production and sales. The supply and demand functions are given, and market equilibrium is defined as the point where supply equals demand. By setting the supply function equal to the demand function, the quantity that should be produced and sold for market equilibrium is found. The equilibrium price is then calculated by substituting the equilibrium quantity into either the supply or demand function. The resulting equilibrium price and quantity, along with a graphical representation of surplus and shortage scenarios, are presented.
📊 Analyzing Market Forces and Equilibrium with Graphical Methods
The fifth paragraph delves into the graphical representation of market forces, specifically supply and demand curves, and how they interact to reach market equilibrium. The impact of different pricing levels on the market is explained, showing how prices can lead to surpluses or shortages. The process of finding the equilibrium point where the quantity demanded matches the quantity supplied is described. An example is given where the supply and demand functions for two-liter sodas are provided, and the calculation for market equilibrium in terms of quantity and price is demonstrated. The resulting equilibrium price and quantity are identified, and a graphical illustration of the supply and demand curves is included to show surplus and shortage areas.
Mindmap
Keywords
💡Functional Models
💡Perimeter
💡Area
💡Quadratic Function
💡Vertex Formula
💡Rational Function
💡Market Equilibrium
💡Surplus
💡Shortage
💡Supply and Demand Functions
💡Graphing Calculator
Highlights
Creating functional models from word problem scenarios to find the largest or smallest values of a function.
Using a farmer's fencing problem to illustrate how to create a rectangle with a given perimeter and find the dimensions for the largest possible area.
Deriving the function for the area of a rectangle from its perimeter and dimensions, then using it to find the maximum area.
Applying the vertex formula for quadratic functions to find the maximum area of a rectangle with a fixed perimeter.
Exploring a variation of the fencing problem where the farmer builds a pin against a barn, changing the perimeter calculation and the resulting dimensions.
Designing an open-top rectangular box with a fixed volume and dimensions to minimize the total cost of materials, considering different costs for lateral sides and the base.
Using calculus and graphing techniques to determine the dimensions and minimum cost of the box, including the use of a graphing calculator.
Discussing market forces and equilibrium, explaining surplus and shortage scenarios and how they relate to supply and demand curves.
Calculating market equilibrium for two-liter sodas using supply and demand functions to find the optimal production and selling price.
Graphically representing supply and demand curves to understand surplus, shortage, and equilibrium points in a market.
Using linear equations to model supply and demand, and solving for market equilibrium to determine production quantities and prices.
Highlighting the practical application of mathematical functions in real-world scenarios such as optimizing areas, minimizing costs, and understanding market dynamics.
Demonstrating the process of substituting variables in functions to simplify complex problems into solvable equations.
Teaching how to use the area of a rectangle and its perimeter to find the dimensions that yield the maximum enclosed space.
Introducing the concept of market equilibrium and its importance in determining the right balance between supply and demand in an economic context.
Providing a step-by-step guide on how to use a graphing calculator to find the minimum value of a function, which is crucial for optimization problems.
Explaining the economic principle of surplus and shortage, showing how price affects the balance between what consumers want and what producers can supply.
Describing the process of setting up and solving equations for supply and demand to find the equilibrium point where the quantity supplied equals the quantity demanded.
Transcripts
Browse More Related Video

Consumers' Surplus Producers' Surplus from given Demand and Supply functions

Calculus 1 Lecture 3.7: Optimization; Max/Min Application Problems

Business Optimization and Elasticity!

Solving for Consumer, Producer, and Social Surplus using Integration
Math 11 - Section 5.1

consumer surplus and producer surplus
5.0 / 5 (0 votes)
Thanks for rating: