Business Optimization and Elasticity!

Ian Grigsby

16 Mar 202016:35

EducationalLearning

32 Likes 10 Comments

TLDRThe video script is an educational discourse on business word problems, focusing on concepts such as cost, revenue, profit, and market dynamics. It begins with a review of essential mathematical formulas related to these business metrics, emphasizing the importance of functions and derivatives in finding maximum and minimum values. The script then delves into an example problem involving a demand function and a cost function to illustrate how to maximize profit. It explains the process of deriving the profit function, applying the first derivative test, and solving for critical points to find the maximum profit. The video also introduces the concept of price elasticity of demand (EDA) as a measure of market responsiveness to price changes, defining elastic, inelastic, and unit elastic markets. It provides a formula for calculating EDA and demonstrates how to determine the market type based on the value of EDA. The summary concludes with a reminder of the key learnings, including the use of derivatives to solve business problems and the interpretation of EDA to understand market behavior.

Takeaways

📈 To find maximum or minimum values in business word problems, you need a function. Once you have the function, you can take its derivative and apply the first or second derivative test to find the max or min.
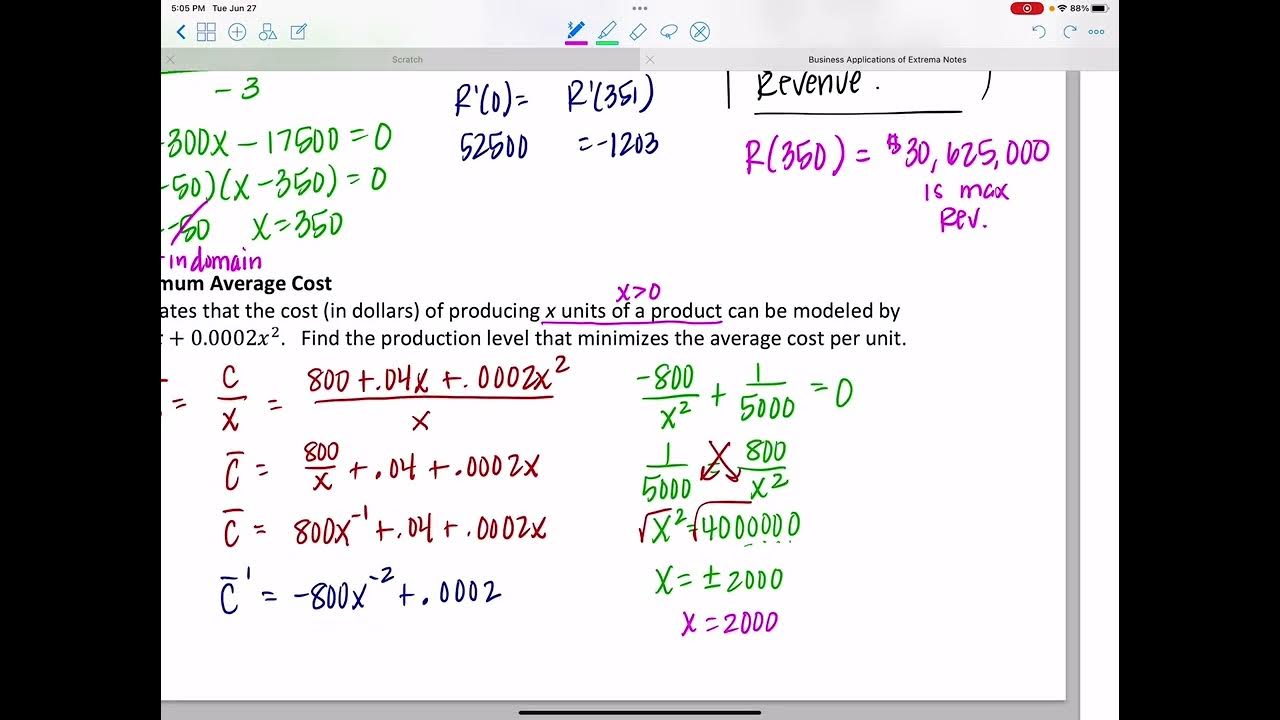
🧮 The average cost (AC) is calculated as the total cost (C of X) divided by the number of items (X). It helps to think of the cost per item when considering the average cost.
💰 Revenue is calculated by multiplying the number of units sold (X) by the price per unit given by the demand function (P of X).
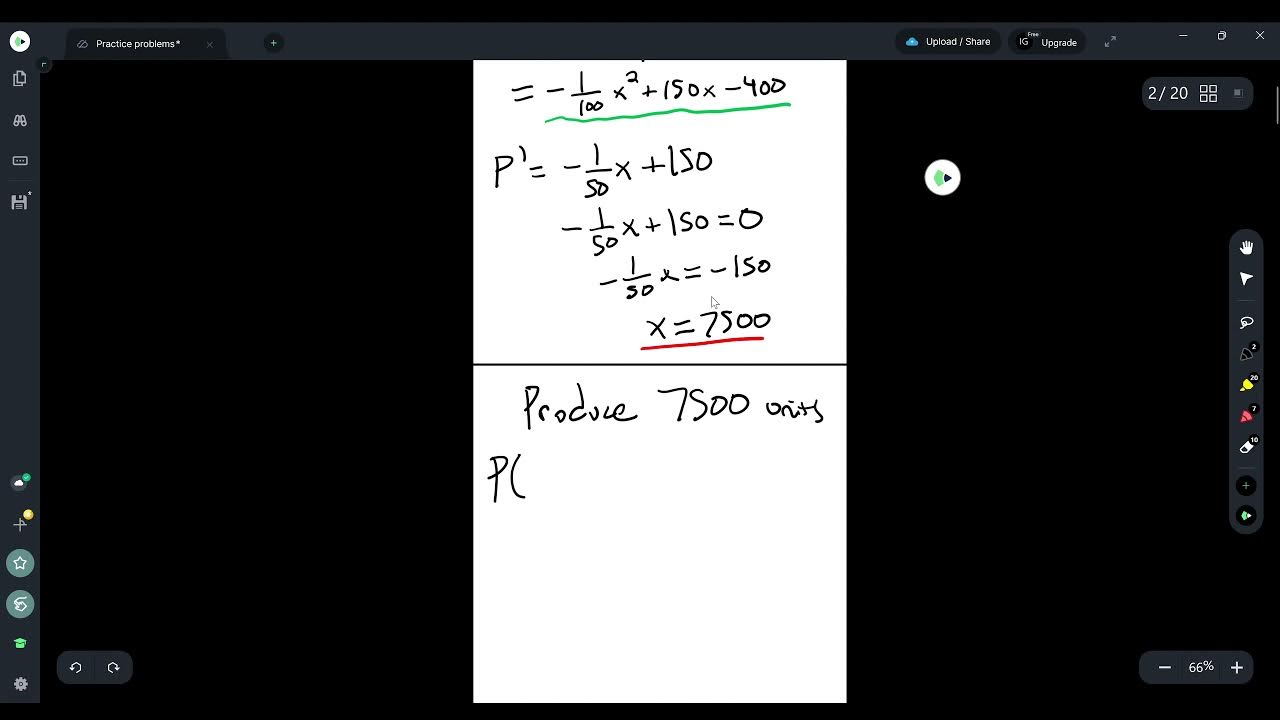
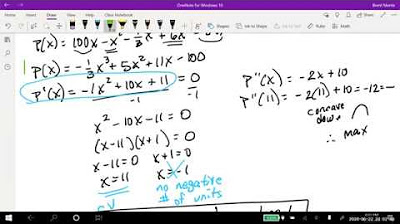
📊 Profit is determined by subtracting the cost (C) from the revenue. Once you have a function for profit, you can find the maximum or minimum profit points.
🔍 In the given example, the demand function is P = 70 - 0.01X, and the cost function is C = 8000 + 50X + 0.03X^2. By combining these, you can find the price that maximizes profit.
✅ The profit function, after simplification, is a quadratic equation with a negative leading coefficient, indicating a downward-opening parabola and thus a maximum value.
🔢 To find the price that maximizes profit, set the derivative of the profit function to zero and solve for X, which in the example is found to be 250 units.
💵 The price that maximizes profit is calculated by substituting the value of X back into the price function, resulting in $67.50 in the given example.
📉 Price elasticity of demand (EDA) measures the responsiveness of consumers to a change in the price of a product. It's calculated using the formula ADA = (P/X) / (dP/dX).
🔁 A market is considered elastic if the absolute value of ADA is greater than 1, inelastic if it's less than 1, and unit elastic if it equals 1.
📌 In the example given, the price elasticity of demand at X equals five units is calculated to be negative five-eighths, indicating an inelastic market.
⏸ In an inelastic market, increasing the price leads to an increase in revenue because consumers continue to buy the product despite the price hike.

Q & A

What is the formula for average cost as discussed in the script?
-The formula for average cost, denoted as C̄(x), is total cost C(x) divided by the number of items x. For example, if you have 20 baseball cards worth a total of $100, the average cost per card is $5.
How is revenue calculated when given a demand function according to the script?
-Revenue is calculated by multiplying the number of units sold (x) by the price per unit (P(x)), which is derived from the demand function. The formula is expressed as Revenue = x * P(x).
What is the basic formula for profit as discussed in the video?
-Profit is calculated by subtracting total costs from total revenue, using the formula Profit = Revenue - Cost.
Can you describe the process to find the maximum profit using derivatives as outlined in the script?
-To find the maximum profit, you first need to define a profit function as Profit = Revenue - Cost. Then, take the first derivative of the profit function to find critical points by setting the derivative equal to zero. Solve for x to find the quantity that maximizes profit. A second derivative test can confirm if it is a maximum by checking if the second derivative is negative, indicating a concave down curve at the critical point.
What is the significance of the downward-opening parabola in determining maximum profit?
-A downward-opening parabola in the context of a profit function indicates that the vertex of the parabola represents a maximum point. This is because the function increases up to the vertex and decreases after, meaning the vertex corresponds to the maximum profit.
What does elasticity of demand measure in economics, as explained in the script?
-Elasticity of demand measures the responsiveness of consumers to changes in the price of a product. It assesses how quantity demanded changes in response to a price change.
How do you determine if a market is elastic, inelastic, or unit elastic using the price elasticity of demand?
-The market is considered elastic if the absolute value of the price elasticity of demand (|η|) is greater than 1, inelastic if less than 1, and unit elastic if it equals 1. This indicates how sensitive the quantity demanded is to price changes.
What example does the script provide to illustrate an inelastic market?
-The script uses the market for insulin as an example of an inelastic market. Since insulin is essential for customers who need it, an increase in its price does not significantly reduce its demand, reflecting a lack of viable substitutes.
How is the price elasticity of demand formula represented and calculated?
-The price elasticity of demand is calculated with the formula η = (P / x) / (dP/dx), where P is the price function and x is the quantity. The derivative dP/dx represents the rate of change of price with respect to the quantity. The formula measures how much the quantity demanded responds to a change in price.
How does the script suggest finding the price elasticity of demand at a specific quantity?
-To find the price elasticity at a specific quantity, first calculate the price and its derivative at that quantity. Then, substitute these values into the elasticity formula η = (P / x) / (dP/dx). For example, if x equals 5, calculate P(5) and dP/dx at x = 5, then substitute these into the formula to get η.

Outlines

00:00

📚 Introduction to Business Word Problems

The first paragraph introduces the topic of business word problems focusing on cost, revenue, profit, and market analysis. It emphasizes the importance of understanding and applying mathematical formulas to find maximum and minimum values in business scenarios. The presenter reviews key formulas such as average cost (C Bar of X), revenue (X times P of X), and profit (revenue minus cost). An example is provided to illustrate how to combine demand, revenue, and cost functions to maximize profit, using a derivative test.

05:01

📈 Maximizing Profit with Derivatives

The second paragraph delves into the process of maximizing profit by finding critical points using derivatives. It explains the steps to derive the profit function, set it equal to zero, and solve for X to find the critical points. The presenter then demonstrates how to use the second derivative test to confirm that the critical point corresponds to a maximum profit. The example concludes with calculating the price that maximizes profit, using the given demand and cost functions.

10:03

📉 Price Elasticity of Demand

The third paragraph discusses the concept of price elasticity of demand (ADA), which measures how responsive consumers are to changes in the price of a product. It differentiates between elastic, inelastic, and unit elastic markets based on the responsiveness to price changes. The presenter provides the formula for calculating ADA and explains how to determine the type of market by evaluating the absolute value of ADA. An example calculation is shown to find the price elasticity of demand at a specific number of units, using the given demand function.

15:05

🔍 Interpreting ADA for Market Behavior

The fourth and final paragraph summarizes the key learnings from the video script. It reiterates the importance of having a function to apply derivative tests for finding maxima and minima in business problems. It also recaps the concept of price elasticity of demand, emphasizing the interpretation of ADA values to understand market behavior. The presenter outlines the implications of different ADA values on revenue in response to price changes and thanks the viewers for watching, promising a discussion on asymptotes in the next session.

Mindmap

Keywords

💡Business Word Problems

Business word problems are practical scenarios that require the application of mathematical concepts to solve real-world business issues. In the video, they are used to demonstrate how to calculate cost, revenue, and profit, which are fundamental to understanding business operations. The script discusses how to formulate these problems into mathematical functions to find their maximum or minimum values, which can help businesses optimize their profits.

💡Cost Function

A cost function, denoted as C(x), represents the total cost of producing 'x' number of items. It's a fundamental concept in the video as it's used to calculate the average cost per item and is a key component in determining profit. The script provides an example where the cost function is given as C = 8000 + 50x + 0.03x^2, which is then used to find the profit-maximizing price.

💡Revenue Function

Revenue function, often denoted as R(x) or P(x) * x, calculates the total income generated from selling 'x' units of a product. It is derived from the product of the number of units sold and the price per unit. In the context of the video, revenue is integral to calculating profit, as it is one of the components subtracted from cost to determine profit.

💡Profit Function

Profit is the difference between revenue and cost. The profit function, which is revenue minus cost, is central to the video's discussion on maximizing business earnings. The script illustrates how to derive a profit function from given demand and cost functions and then uses calculus to find the price that maximizes profit.

💡Derivative Test

The derivative test is a method used in calculus to find the maximum or minimum values of a function. In the context of the video, it is applied to find the quantity of units that will maximize profit. By taking the derivative of the profit function and setting it to zero, one can find critical points that may represent maximum or minimum profit.

💡Quadratic Function

A quadratic function is a polynomial function of degree two. Its general form is f(x) = ax^2 + bx + c, where a, b, and c are constants. In the video, the profit function is simplified to a quadratic form, which helps identify that the profit function represents a downward-opening parabola, indicating a maximum profit can be found.

💡Price Elasticity of Demand (PED)

Price Elasticity of Demand (PED) is a measure of how sensitive the quantity demanded of a good is to a change in its price. It is calculated as the percentage change in quantity demanded divided by the percentage change in price. In the video, PED is used to determine whether a market is elastic, inelastic, or unit elastic, which has significant implications for pricing strategies.

💡Elastic Market

An elastic market is one where the demand for a product is highly responsive to price changes. If the price increases, the quantity demanded decreases significantly, leading to a potential decrease in total revenue. The video uses the example of a Snickers bar to illustrate an elastic market, where consumers have many alternatives and are sensitive to price changes.

💡Inelastic Market

An inelastic market is one where demand does not significantly change with price alterations. Even if the price increases, consumers continue to purchase the product due to a lack of substitutes or necessity. The video uses the example of insulin to illustrate an inelastic market, where consumers have little choice but to purchase the product regardless of price increases.

💡Unit Elastic

A unit elastic market is one where the percentage change in quantity demanded is equal to the percentage change in price. In such a market, a change in price does not affect the total revenue because the percentage increase in price is exactly offset by the percentage decrease in quantity demanded. The video explains that if the absolute value of PED is exactly one, the market is unit elastic.

💡First and Second Derivative Tests

The first and second derivative tests are methods from calculus used to determine the nature of critical points of a function. The first derivative test involves finding where the derivative is zero or undefined and the second derivative test involves analyzing the sign of the second derivative at those points. In the video, these tests are used to find the quantity of units that will result in the maximum profit for a business.

Highlights

Introduction to business word problems involving cost, revenue, profit, and market analysis.

Review of key formulas for finding maximum and minimum values using derivatives.

Explanation of average cost function and its calculation.

Revenue function and its relation to the demand function and the number of units sold.

Profit function defined as the difference between revenue and cost.

Example problem demonstrating how to find the price that maximizes profit using a given demand and cost function.

Derivation of the profit function and application of the first derivative test to find critical points.

Calculation of the second derivative to confirm the presence of a maximum profit point.

Determination of the price that maximizes profit by substituting the critical point into the price function.

Introduction to the concept of price elasticity of demand and its importance in market responsiveness.

Definition of market elasticity terms: elastic, inelastic, and unit elastic.

Formula for calculating the price elasticity of demand (ADA) and its practical application.

Method to determine if a market is inelastic, elastic, or unit elastic by evaluating the absolute value of ADA.

Example calculation of price elasticity of demand at a specific number of units.

Interpretation of ADA values to understand market behavior in response to price changes.

Implications of inelastic, elastic, and unit elastic markets on pricing strategy and revenue.

Summary of learning outcomes including business problem-solving using calculus and understanding price elasticity of demand.

Preview of the next topic: horizontal and vertical asymptotes with limits as we approach infinity.

Transcripts

Browse More Related Video

Business Calculus - Section 3.4 - Optimization and Elasticity of Demand

Business Applications of Extrema

Optimization Problem Examples

Math 11 - Section 3.5

Marginal Revenue, Average Cost, Profit, Price & Demand Function - Calculus

BusCalc 10 Marginal Profit