Solving for Consumer, Producer, and Social Surplus using Integration
TLDRThis video delves into the application of integration in economic theory, focusing on consumer, producer, and social surplus. It explains how these concepts measure welfare in a market, particularly highlighting that a perfectly competitive market maximizes social surplus. The script uses integral calculus to calculate surpluses, providing formulas and an example with given demand and supply functions. It guides through finding equilibrium price and quantity, then computes consumer and producer surplus, concluding with social surplus as their sum, demonstrating the mathematical approach to economic analysis.
Takeaways
- 📚 The video discusses the application of integration in determining consumer, producer, and social surplus in microeconomic theory.
- 💡 Consumer surplus represents the welfare of consumers and is the amount they are willing to pay but do not, due to the equilibrium price.
- 📈 The formula for calculating consumer surplus is the integral from zero to the equilibrium quantity of the demand function, minus the area of the rectangle formed by the equilibrium price and quantity.
- 🔍 Producer surplus represents the welfare of producers and is the amount they receive above what they are willing to accept.
- 📐 The formula for calculating producer surplus is the total revenue at the equilibrium price minus the integral from zero to the equilibrium quantity of the supply function.
- 🤝 Social surplus is the sum of consumer and producer surplus, representing the overall welfare of the economy.
- 📉 In a perfectly competitive market, the highest consumer surplus and zero producer surplus theoretically result in the highest social surplus.
- 📚 The video uses an example with a given market demand function p = 50 - 0.1q and market supply function p = 0.2q + 20 to illustrate the calculation of surpluses.
- 🧩 The first step in the example is to calculate the equilibrium quantity and price by setting the market supply equal to the market demand.
- 🔢 The equilibrium quantity is found to be 100, and the equilibrium price is calculated to be 40 by substituting the quantity into the demand function.
- 📉 The consumer surplus is calculated to be 500, the producer surplus 1000, and the social surplus 1500 using integration techniques.
Q & A
What is the main topic of the video?
-The main topic of the video is the application of integration in determining the concepts of consumer surplus, producer surplus, and social surplus in microeconomic theory.
Why are consumer surplus, producer surplus, and social surplus important in microeconomics?
-Consumer surplus, producer surplus, and social surplus are important in microeconomics as they are critical concepts for measuring the level of welfare in an economy, particularly in the context of market efficiency.
What is consumer surplus?
-Consumer surplus represents the welfare of consumers and is the extra amount that consumers would have been willing to pay but did not, due to paying the equilibrium price instead.
How is consumer surplus calculated?
-Consumer surplus is calculated as the integral from zero to the equilibrium quantity (q*) of the demand function, minus the area of the rectangle formed by the equilibrium price (p*) times the equilibrium quantity (q*).
What does producer surplus represent?
-Producer surplus represents the welfare of producers or sellers and is the extra amount they receive above the price they are willing to accept.
How is producer surplus calculated?
-Producer surplus is calculated as the area of the rectangle formed by the equilibrium price (p*) times the equilibrium quantity (q*), minus the integral from zero to the equilibrium quantity (q*) of the supply function.
What is social surplus?
-Social surplus is the sum of consumer surplus and producer surplus, and it serves as a welfare measure of the whole economy, assuming the economy is composed of producers and consumers.
How is social surplus calculated using integration?
-Social surplus is calculated by adding the consumer surplus and producer surplus together. In terms of integration, it is the integral from zero to the equilibrium quantity (q*) of the demand curve minus the integral of the area under the supply curve.
What are the equilibrium price and quantity?
-The equilibrium price and quantity are the values at which the market supply equals the market demand, indicating a balance between what consumers are willing to buy and what producers are willing to sell.
Can you provide an example of how to calculate consumer surplus using the given demand function?
-Yes, using the demand function p = 50 - 0.1q, the consumer surplus is calculated by integrating from 0 to 100 (the equilibrium quantity) of the demand function and subtracting the area of the rectangle formed by p*q*, which results in a consumer surplus of 500.
How do you calculate the producer surplus using the given supply function?
-Using the supply function s = 0.2q + 20, the producer surplus is calculated by taking the product of the equilibrium price and quantity (4000) and subtracting the integral from 0 to 100 of the supply function, which results in a producer surplus of 1000.
Outlines
📚 Introduction to Consumer, Producer, and Social Surplus
This paragraph introduces the video's focus on the applications of integration in determining concepts of consumer, producer, and social surplus in microeconomic theory. The speaker emphasizes the importance of these concepts in measuring welfare levels within a market. It is explained that in a perfectly competitive market, consumer surplus is maximized, and producer surplus is zero, leading to the highest social surplus, which is a measure of market efficiency and overall welfare. The video aims to explore these concepts using integral calculus.
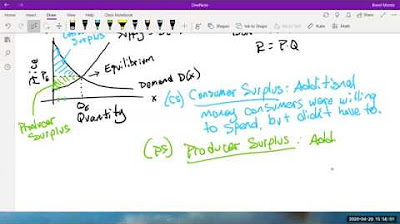
📈 Calculating Consumer and Producer Surplus Using Integration
The speaker delves into the methodology of calculating consumer and producer surplus through integration. Consumer surplus is defined as the difference between what consumers are willing to pay and the equilibrium price, represented graphically as the area under the demand curve above the equilibrium price. Producer surplus is the difference between the equilibrium price and what producers are willing to accept, shown as the area above the supply curve up to the equilibrium price. The formulas for calculating these surpluses are presented, involving integrals of the demand and supply functions and subtraction of the respective areas representing the surplus.
🔢 Example Calculation of Equilibrium Price and Quantity
In this paragraph, the speaker provides an example to illustrate the calculation of consumer, producer, and social surplus. Given a market demand function and a market supply function, the first step is to find the equilibrium quantity and price by setting the demand equal to the supply. The example involves algebraic manipulation to solve for the equilibrium quantity (q*) and then substituting it back into either the demand or supply function to find the equilibrium price (p*). The calculations lead to an equilibrium quantity of 100 and an equilibrium price of 40.
📉 Deriving Consumer and Producer Surplus from the Example
Building on the previous paragraph, the speaker calculates the consumer surplus by integrating the demand function from 0 to the equilibrium quantity and subtracting the area represented by the equilibrium price times the equilibrium quantity. The producer surplus is calculated by subtracting the integral of the supply function from the product of the equilibrium price and quantity. The calculations for both surpluses are shown step by step, resulting in a consumer surplus of 500 and a producer surplus of 1000.
💡 Conclusion: Social Surplus as the Sum of Consumer and Producer Surplus
The final paragraph concludes the video by defining social surplus as the sum of consumer and producer surplus, which in the given example amounts to 1500. The speaker wraps up by summarizing the process of calculating these surpluses and hints at further exploration of integration applications in economics in future videos. The aim is to demonstrate how these mathematical tools can be applied to economic theories to measure welfare and efficiency within different market structures.
Mindmap
Keywords
💡Integration
💡Consumer Surplus
💡Producer Surplus
💡Social Surplus
💡Market Equilibrium
💡Demand Curve
💡Supply Curve
💡Welfare Economics
💡Perfect Competition
💡Equilibrium Quantity and Price
💡Law of Demand and Supply
Highlights
Introduction to the application of integration in determining consumer, producer, and social surplus.
Explanation of consumer surplus as the extra amount consumers would have been willing to pay but did not because they paid the equilibrium price.
Visual representation of the consumer surplus area under the demand curve above the equilibrium price.
Definition and graphical representation of producer surplus as the extra amount producers receive above the price they were willing to accept.
Description of social surplus as the sum of consumer and producer surplus, representing the total welfare in the economy.
Integral formula for calculating consumer surplus: the area under the demand curve minus the area of the equilibrium price and quantity.
Integral formula for calculating producer surplus: the area of the equilibrium price and quantity minus the area under the supply curve.
Calculation steps for determining equilibrium quantity and price by equating market demand and supply functions.
Example problem: given market demand and supply functions, calculating equilibrium quantity and price.
Step-by-step calculation of consumer surplus using the given market demand function.
Step-by-step calculation of producer surplus using the given market supply function.
Final calculation of social surplus as the sum of consumer and producer surplus.
Emphasis on the importance of understanding consumer, producer, and social surplus for measuring market efficiency and welfare.
Application of integration in economics to solve practical problems related to market structures and welfare.
Encouragement to explore further applications of integration in economics and mathematics in succeeding videos.
Transcripts
Browse More Related Video

Consumers' Surplus Producers' Surplus from given Demand and Supply functions
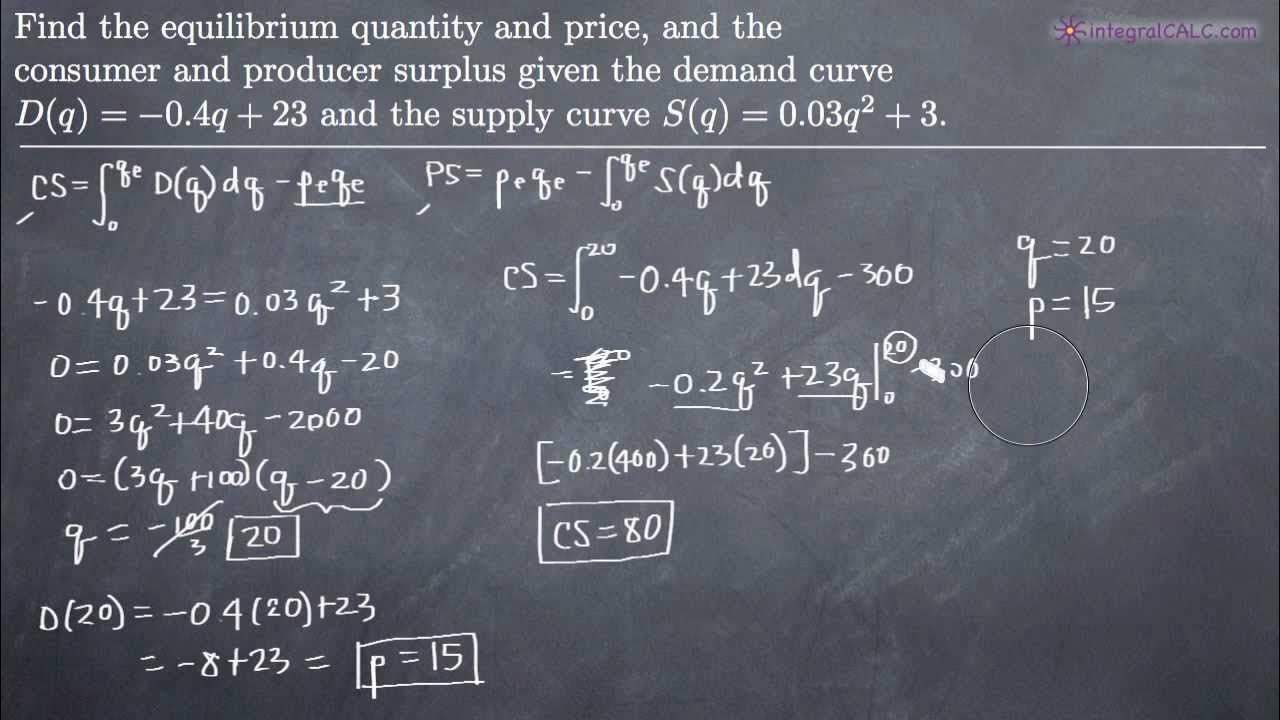
Consumer and Producer Surplus (KristaKingMath)
Math 11 - Section 5.1

consumer surplus and producer surplus

Consumers 'surplus Producers' Surplus , Total surplus, deadweight loss with price floor

Consumer Surplus and Producer Surplus
5.0 / 5 (0 votes)
Thanks for rating: