Finding a Horizontal Asymptote of a Rational Function (Precalculus - College Algebra 40)
TLDRThis video script delves into the concept of horizontal asymptotes in rational functions, a key topic in calculus. The presenter explains that horizontal asymptotes are similar to vertical asymptotes but are horizontal lines that a function approaches but never touches. To determine the presence and type of a horizontal asymptote, one must compare the degrees of the leading terms of the numerator and denominator. If the degree of the denominator is greater, a horizontal asymptote at y=0 exists. If the degrees are equal, the asymptote is at y equals the ratio of the leading coefficients. The script also touches on the idea of end behavior, explaining that rational functions can exhibit one of three types: a horizontal asymptote, a slant asymptote (when the numerator's degree is one more than the denominator's), or no asymptote, leading to end behavior resembling a polynomial. The presenter emphasizes the importance of understanding limits and how they dictate the function's behavior as it approaches positive or negative infinity. The script is educational, aiming to provide a deep understanding of the topic rather than just memorization of formulas.
Takeaways
- 📊 To determine a horizontal asymptote in a rational function, compare the degrees of the leading terms of the numerator and the denominator.
- 🔍 If the degree of the denominator is greater than the degree of the numerator, there is a horizontal asymptote at y=0.
- 📌 When the degrees are equal, the horizontal asymptote is at y equals the ratio of the leading coefficients.
- 🔢 The end behavior of a rational function is determined by the leading terms of the numerator and denominator.
- ∞ As x approaches positive or negative infinity, the function's behavior is dictated by the simplified ratio of the leading terms.
- 🚫 A rational function cannot have both a horizontal and a slant asymptote; it's one or the other, or neither.
- ✅ Simplifying the ratio of the leading terms helps in understanding the end behavior and determining the horizontal asymptote.
- 🤔 Thinking critically about what happens when x becomes extremely large or small is crucial for understanding limits and asymptotes.
- 🚧 A horizontal asymptote can be crossed, unlike a vertical asymptote, which represents an undefined value.
- 📈 In the case where the degree of the numerator is larger by one, the function will have a slant or oblique asymptote, which is a diagonal line.
- ➕ If the degree of the numerator is larger by more than one, the end behavior of the function will resemble a parabola.
Q & A
What is a horizontal asymptote?
-A horizontal asymptote is a horizontal line that a function approaches as its input (x-values) approaches positive or negative infinity. It represents the end behavior of a rational function.
How is a horizontal asymptote determined for a rational function?
-A horizontal asymptote is determined by comparing the degrees of the leading terms of the numerator and the denominator of the rational function. If the degree of the denominator is greater than the degree of the numerator, the horizontal asymptote is at y=0. If they are equal, the horizontal asymptote is at y equals the ratio of the leading coefficients.
What is the difference between a vertical asymptote and a horizontal asymptote?
-A vertical asymptote is a line that the function cannot cross, acting like a force field, whereas a horizontal asymptote is a line that the function can approach and even cross as it extends to positive or negative infinity.
Why can a function cross a horizontal asymptote?
-A function can cross a horizontal asymptote because, unlike a vertical asymptote, the function's behavior as it approaches positive or negative infinity allows it to get arbitrarily close to, but not exactly on, the horizontal line representing the asymptote.
What is the end behavior of a rational function?
-The end behavior of a rational function refers to how the function behaves as the input (x-values) approaches positive or negative infinity. It can be determined by looking at the leading terms of the numerator and the denominator.
How does the degree of the numerator compare to the degree of the denominator to determine the horizontal asymptote?
-If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y=0. If the degrees are equal, the horizontal asymptote is at y equals the ratio of the leading coefficients of the numerator and the denominator.
What is an oblique or slant asymptote?
-An oblique or slant asymptote is a diagonal line that a rational function approaches as its input (x-values) approaches positive or negative infinity. This occurs when the degree of the numerator is exactly one greater than the degree of the denominator.
What happens if the degree of the numerator is larger than the degree of the denominator by more than one?
-If the degree of the numerator is larger than the degree of the denominator by more than one, the end behavior of the function will resemble that of a polynomial with the same degree as the numerator, and there will be no horizontal or slant asymptote.
Why do we simplify the ratio of the leading terms of a rational function to determine its end behavior?
-Simplifying the ratio of the leading terms allows us to consider the behavior of the function as x becomes very large (positive or negative), which is easier to conceptualize than dealing with the full polynomial expressions. This simplification helps us to identify the horizontal asymptote and the end behavior of the function.
What is the significance of limits in understanding the behavior of a function as x approaches infinity?
-Limits are a fundamental concept in calculus that describe the behavior of a function as the input (x-values) approaches a particular value. In the context of horizontal asymptotes, limits help us understand what value the function approaches (but never actually reaches) as x becomes infinitely large or small.
Can a function have both a horizontal asymptote and a slant asymptote?
-No, a function cannot have both a horizontal asymptote and a slant asymptote. The function's end behavior will be categorized into one of the three types: a horizontal asymptote, a slant asymptote, or another type of end behavior that does not include an asymptote.
Outlines
📚 Introduction to Horizontal Asymptotes
The video begins by introducing the topic of horizontal asymptotes in rational functions. The presenter explains that horizontal asymptotes are similar to vertical asymptotes but are horizontal lines that the function never touches. The focus is on determining when a rational function has a horizontal asymptote by examining the leading terms of the numerator and denominator. If the degree of the denominator is greater than the degree of the numerator, there is a horizontal asymptote at y=0. If the degrees are equal, the horizontal asymptote is at the ratio of the leading coefficients.
🔍 Understanding End Behavior and Asymptotes
This paragraph delves into the concept of end behavior in rational functions, explaining how it is determined by the leading terms of the numerator and denominator. The presenter clarifies that there are three types of end behavior: a horizontal asymptote, a slant (or oblique) asymptote, and a cubic or quadratic end behavior. It is emphasized that a function cannot have both a horizontal and a slant asymptote simultaneously. The importance of understanding the degree of the denominator and numerator in relation to the horizontal asymptote is discussed, along with a practical example to illustrate the concept.
🧮 Simplifying Rational Functions to Determine Asymptotes
The presenter explains how to simplify rational functions by focusing on the leading terms and their degrees. It is shown that power functions with the same variable can always be simplified, and this simplification helps in understanding the end behavior of the function. The video illustrates why a horizontal asymptote at y=0 occurs when the degree of the denominator is greater than the numerator. The concept of limits is introduced to explain the behavior of the function as x approaches positive or negative infinity.
🏞️ Horizontal Asymptotes and Their Characteristics
This section further explores horizontal asymptotes, emphasizing that they are different from vertical asymptotes because they can be crossed by the function. The video explains that while a function cannot touch a vertical asymptote, it can cross a horizontal asymptote. The presenter also discusses the behavior of the function as x approaches large positive or negative values and how this relates to the horizontal asymptote. The concept of limits is again used to describe the function's behavior as it approaches the asymptote.
🔢 Analyzing the Degrees of Numerator and Denominator
The video continues with an example to show how to determine the type of horizontal asymptote present in a rational function. It is explained that if the degrees of the numerator and denominator are equal, the horizontal asymptote is the ratio of the leading coefficients. The presenter simplifies the example and uses it to demonstrate how the function approaches the horizontal asymptote as x approaches positive and negative infinity. The importance of understanding the direction in which the function approaches the asymptote is also discussed.
🏡 Conclusion and Preview of Upcoming Topics
In the final paragraph, the presenter summarizes the key points about horizontal asymptotes and their determination through the comparison of degrees in the numerator and denominator. It is reiterated that if the degree of the denominator is larger, the horizontal asymptote is at y=0, and if the degrees are equal, the asymptote is at the ratio of the leading coefficients. The video concludes with a preview of upcoming topics, which include oblique (or slant) asymptotes and more complex end behaviors. The presenter emphasizes the importance of grasping the basics before moving on to more advanced concepts.
Mindmap
Keywords
💡Rational Function
💡Horizontal Asymptote
💡Degree of a Polynomial
💡Leading Term
💡End Behavior
💡Limit
💡Simplifying Rational Functions
💡Oblique/Slant Asymptote
💡Numerator and Denominator
💡Vertical Asymptote
💡Coefficients
Highlights
A rational function's horizontal asymptote can be determined by comparing the degrees of the leading terms of the numerator and denominator.
If the degree of the denominator is larger than the numerator, a horizontal asymptote at y=0 exists.
When the degrees are equal, the horizontal asymptote is located at the ratio of the leading coefficients.
End behavior of a rational function is determined by its leading terms.
A horizontal asymptote can be crossed, unlike a vertical asymptote which is undefined at the point of intersection.
The concept of limits is crucial in understanding the behavior of functions as x approaches positive or negative infinity.
Simplifying the ratio of leading terms can provide insight into the end behavior of the function.
A horizontal asymptote at y=0 occurs when the constant term (numerator) remains the same while the variable term (denominator) grows larger.
When the degrees of the numerator and denominator are the same, the variables cancel out, resulting in a constant horizontal asymptote.
The function's value approaches the horizontal asymptote as x tends to positive or negative infinity but never actually reaches it.
The direction in which the function approaches the horizontal asymptote can vary and may require further mathematical analysis.
If the degree of the numerator is larger by one, an oblique or slant asymptote may occur, which is a diagonal line.
For a numerator degree larger by more than one, the end behavior of the function will resemble a parabola.
The video provides a deep understanding of why horizontal asymptotes occur and how to calculate them.
The importance of understanding limits in calculus is emphasized for grasping the concept of horizontal asymptotes.
The video explains the theoretical underpinnings behind the rules for determining horizontal asymptotes.
Practical examples are used to illustrate the process of determining horizontal asymptotes and their types.
Transcripts
Browse More Related Video

Finding an Oblique Asymptote of a Rational Function (Precalculus - College Algebra 41)

Horizontal Asymptotes and Slant Asymptotes of Rational Functions
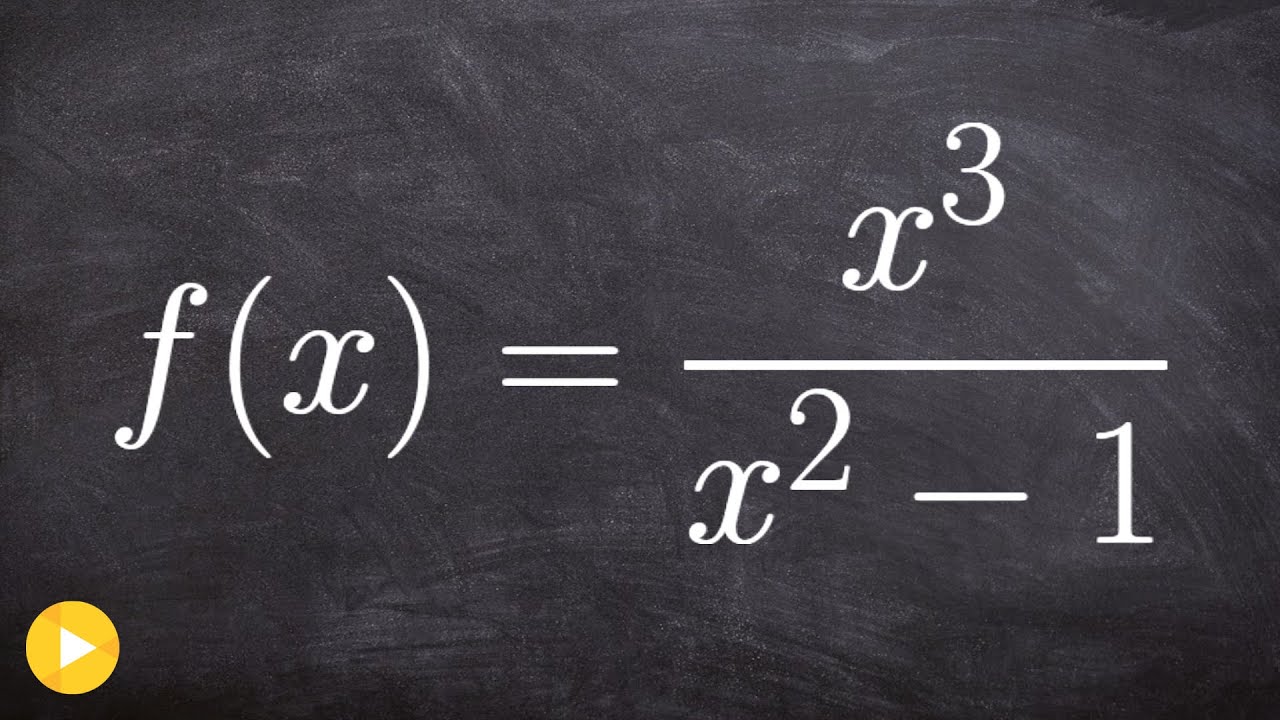
Finding the Slant Asymptote
Graphing Rational Functions and Their Asymptotes

Horizontal and Vertical Asymptotes - Slant / Oblique - Holes - Rational Function - Domain & Range

How to graph a rational function using 6 steps
5.0 / 5 (0 votes)
Thanks for rating: