Finding an Oblique Asymptote of a Rational Function (Precalculus - College Algebra 41)

Professor Leonard
6 Oct 202015:46
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of oblique, or slant, asymptotes in rational functions. It emphasizes that understanding horizontal asymptotes and end behavior is crucial before tackling oblique asymptotes. The script explains that oblique asymptotes occur when the degree of the numerator is exactly one more than the degree of the denominator, resulting in a diagonal line that the function approaches as x tends to infinity or negative infinity. The presenter highlights the necessity of knowing long division of polynomials, as synthetic division is insufficient for this task. The process of finding the oblique asymptote involves performing long division twice to obtain the slope-intercept form (y = mx + b) of the asymptote. The script clarifies that a function cannot have both a horizontal and an oblique asymptote simultaneously due to the contradiction in degrees. Finally, it is noted that functions can cross an oblique asymptote multiple times, unlike a vertical asymptote, and the asymptote guides the function's behavior towards infinity.

Takeaways
  • πŸ“š Understand what a horizontal asymptote is and when you get them.
  • πŸ” Recognize that oblique (or slant) asymptotes are diagonal lines that a function approaches as x approaches infinity.
  • πŸ“ˆ Learn how to perform long division of polynomials, as synthetic division is insufficient for finding oblique asymptotes.
  • πŸ”’ Remember that oblique asymptotes occur when the degree of the numerator is exactly one more than the degree of the denominator.
  • 🚫 Know that you cannot have both a horizontal and an oblique asymptote at the same time due to the contradiction in degrees.
  • πŸ“‰ Realize that if the degree of the numerator is larger, you have three possibilities: a horizontal asymptote, an oblique asymptote, or just end behavior.
  • πŸ”‘ The leading terms of a rational function determine the end behavior, and for oblique asymptotes, you'll end up with a line after long division.
  • πŸ“ An oblique asymptote is represented as y = mx + b, where m is the slope and b is the y-intercept, found through long division.
  • βœ… After performing long division, you only need to do it twice to find the slope and y-intercept for the oblique asymptote.
  • β›” Be aware that oblique asymptotes can be crossed by the function, unlike vertical asymptotes.
  • πŸ“‰ At the end behavior, the function will follow the diagonal line of the oblique asymptote as x approaches positive or negative infinity.
Q & A

  • What is an oblique asymptote?

    -An oblique asymptote, also known as a slant asymptote, is a diagonal line that a rational function approaches as x approaches positive or negative infinity. It occurs specifically when the degree of the numerator of the function is exactly one more than the degree of the denominator.

  • Why is long division of polynomials necessary for finding an oblique asymptote?

    -Long division of polynomials is necessary because it allows us to determine the slope and y-intercept of the oblique asymptote. Synthetic division is not sufficient for this purpose as it does not provide the full quotient needed to model the end behavior of the function.

  • How do you know when a rational function has an oblique asymptote?

    -A rational function has an oblique asymptote when the degree of the numerator is exactly one greater than the degree of the denominator. In all other cases, the function will either have a horizontal asymptote or exhibit end behavior without an asymptote.

  • What is the general form of the equation for an oblique asymptote?

    -The general form of the equation for an oblique asymptote is y = mx + b, where m represents the slope of the line and b is the y-intercept.

  • Can a function have both a horizontal and an oblique asymptote?

    -No, a function cannot have both a horizontal and an oblique asymptote. The two types of asymptotes are mutually exclusive and depend on the relative degrees of the numerator and denominator of the function.

  • What happens when the degree of the numerator is larger than the degree of the denominator by more than one?

    -When the degree of the numerator is larger than the degree of the denominator by more than one, the function exhibits end behavior without an asymptote. It does not approach a line or a constant value as x approaches infinity.

  • How does the end behavior of a rational function relate to its asymptotes?

    -The end behavior of a rational function is closely tied to its asymptotes. If the degree of the numerator is less than or equal to the degree of the denominator, the function has a horizontal asymptote. If the degree of the numerator is exactly one more than the degree of the denominator, the function has an oblique asymptote. In all other cases, the function simply exhibits end behavior without an asymptote.

  • What is the role of the leading terms in determining the end behavior of a rational function?

    -The leading terms of the numerator and the denominator determine the end behavior of a rational function. They dictate whether the function will have a horizontal asymptote, an oblique asymptote, or simply exhibit end behavior without an asymptote.

  • Can a rational function cross its oblique asymptote?

    -Yes, a rational function can cross its oblique asymptote. Unlike a vertical asymptote, an oblique asymptote is not a barrier that the function cannot cross; the function's graph can intersect the oblique asymptote at one or more points.

  • How many steps are required in long division of polynomials to find the oblique asymptote?

    -For finding the oblique asymptote, only two steps of long division are required. The first step involves dividing the first term of the numerator by the first term of the denominator and then performing the necessary subtraction. The second step is to divide the new first term of the numerator by the first term of the denominator again.

  • What is the significance of the y-intercept in the equation of an oblique asymptote?

    -The y-intercept in the equation of an oblique asymptote is the point where the asymptote would intersect the y-axis if extended. It is derived from the remainder of the long division process and, along with the slope (m), helps to fully define the line that the function approaches at infinity.

Outlines
00:00
πŸ“š Introduction to Oblique Asymptotes

This paragraph introduces the concept of oblique asymptotes, also known as slant asymptotes, which are diagonal lines that a function approaches as x tends to positive or negative infinity. It emphasizes the importance of understanding horizontal asymptotes and the end behavior of rational functions. The video explains that oblique asymptotes occur when the degree of the numerator is exactly one more than the degree of the denominator. It also mentions that long division of polynomials is required to find the oblique asymptote, not synthetic division, and that there are only three cases for the end behavior of a rational function: a horizontal asymptote, an oblique asymptote, or regular end behavior.

05:02
πŸ” Understanding End Behavior and Oblique Asymptotes

The paragraph delves into how the end behavior of a rational function is modeled by its leading terms, which are power functions. It discusses that when the degree of the numerator is one more than the degree of the denominator, an oblique asymptote is present. The paragraph explains that this asymptote is a diagonal line that the function will approach as x increases or decreases without bound. The process of finding the oblique asymptote involves performing long division to find the quotient, which represents the asymptote's equation in the form y = mx + b, where m is the slope and b is the y-intercept.

10:03
πŸ”’ Performing Long Division to Find the Oblique Asymptote

This section provides a step-by-step guide on how to perform long division of polynomials to find the oblique asymptote. It clarifies that only two iterations are needed: dividing the first term of the numerator by the first term of the denominator and then dividing the new first term by the divisor's first term. The process is illustrated with an example, showing that the goal is to find the form y = mx + b, which represents theζ–œ asymptote. The paragraph also notes that the degree of the numerator being one more than the degree of the denominator guarantees a power of one in the first term of the quotient, resulting in a diagonal line.

15:06
🚫 Conditions for Oblique Asymptotes and Upcoming Topics

The final paragraph reiterates that an oblique asymptote is only possible when the degree of the numerator is exactly one more than the degree of the denominator. It also states that you cannot have both a horizontal and an oblique asymptote at the same time due to the contradiction it would present. The speaker previews that after covering oblique asymptotes, the video series will focus on pure end behavior, where neither oblique nor horizontal asymptotes are present. Lastly, the paragraph teases the next topic, which involves functions with even higher degrees in the numerator, leading to different types of end behavior such as parabolas.

Mindmap
Keywords
πŸ’‘Horizontal Asymptote
A horizontal asymptote is a horizontal line that a function approaches as its input (x) approaches either positive or negative infinity. In the video, it is mentioned as the first case of end behavior for rational functions, where the degree of the denominator is equal to or greater than the numerator. An example given is y equals zero, which is the x-axis.
πŸ’‘Oblique Asymptote
An oblique, or slant, asymptote is a diagonal line that a rational function approaches as x approaches positive or negative infinity. It occurs when the degree of the numerator is exactly one more than the degree of the denominator. The video explains that this type of asymptote is significant for modeling the end behavior of a function.
πŸ’‘Long Division of Polynomials
Long division of polynomials is a method used to simplify rational functions and find their oblique asymptotes. It involves dividing the numerator polynomial by the denominator polynomial. The video emphasizes the importance of knowing how to perform this operation, as synthetic division is not sufficient for finding oblique asymptotes.
πŸ’‘End Behavior
End behavior refers to how a rational function behaves as the input (x) approaches very large or very small values, that is, as x approaches positive or negative infinity. The video discusses three cases of end behavior: horizontal asymptotes, oblique asymptotes, and just 'straight up' end behavior where neither a horizontal nor oblique asymptote is present.
πŸ’‘Degree of a Polynomial
The degree of a polynomial is the highest power of the variable in the polynomial. It is crucial in determining the type of end behavior a rational function will exhibit. For instance, if the degree of the numerator is larger by one than the degree of the denominator, an oblique asymptote is present, as discussed in the video.
πŸ’‘Leading Terms
The leading terms of a polynomial are the terms with the highest power of the variable. These terms are significant in determining the end behavior of a function. In the context of the video, the leading terms dictate whether a function will have a horizontal or oblique asymptote.
πŸ’‘Slant Asymptote
A slant asymptote is an informal term for an oblique asymptote. It is used interchangeably in some contexts to describe a diagonal line that a function approaches as x becomes very large or very small. The video mentions this term as an alternative to 'oblique asymptote'.
πŸ’‘Limit
In the context of the video, a limit refers to the value that a function approaches as the input (x) approaches a particular value, such as positive or negative infinity. Limits are integral to understanding end behavior and asymptotes, as they help describe what happens to a function at the 'ends' of its domain.
πŸ’‘Power Functions
Power functions are functions of the form f(x) = ax^n, where a and n are constants. They are important in the video because the leading terms of polynomials, which determine end behavior, are power functions. The script mentions that when the degree of the numerator is one more than the denominator, the leading terms simplify to a power function, resulting in an oblique asymptote.
πŸ’‘Slope
Slope, in the context of the video, refers to the steepness of a line, which is the oblique asymptote in this case. The slope is a key characteristic of the oblique asymptote, indicating how quickly the function increases or decreases along the diagonal line as x changes. The video uses the term to describe the diagonal line that the function approaches.
πŸ’‘Y-Intercept
The y-intercept is the point where a line crosses the y-axis. In the context of the video, the y-intercept is a part of the oblique asymptote's equation, which is found by performing long division of the polynomials in the numerator and denominator of the rational function. The y-intercept, along with the slope, defines the oblique asymptote's line.
Highlights

Introduction to oblique asymptotes, also known as slant asymptotes, which are diagonal lines that a function approaches.

Understanding end behavior of a rational function, which involves three cases: horizontal asymptotes, oblique asymptotes, and regular end behavior.

The importance of knowing how to perform long division of polynomials, not just synthetic division, for finding oblique asymptotes.

Conditions for an oblique asymptote: the degree of the numerator must be exactly one more than the degree of the denominator.

Oblique asymptotes are characterized by a diagonal line that the function approaches as x tends to positive or negative infinity.

Explanation of why the leading terms of a rational function determine the end behavior, particularly when the numerator's degree is larger by one.

The process of performing long division to find the oblique asymptote involves dividing the first term of the numerator by the first term of the denominator.

The result of the long division gives the slope of the oblique asymptote, which is a line with a power of one.

The y-intercept of the oblique asymptote is obtained from the remainder of the long division process.

A function can cross an oblique asymptote, unlike a vertical asymptote, and it may cross it multiple times.

The function's end behavior will follow the oblique asymptote as it approaches positive or negative infinity.

The concept that you cannot have both a horizontal and an oblique asymptote at the same time due to degree contradictions.

The three possible end behavior cases for a rational function: horizontal constant or zero, oblique, or just straight end behavior.

Demonstration of how to perform the long division process step by step to find the oblique asymptote.

Emphasis on the fact that only two iterations of long division are needed to find the oblique asymptote.

The final form of the oblique asymptote is given as y = mx + b, where m is the slope and b is the y-intercept.

A practical example of how to apply the long division method to find the oblique asymptote of a specific rational function.

Transcripts

Browse More Related Video

Horizontal Asymptotes and Slant Asymptotes of Rational Functions

Finding a Horizontal Asymptote of a Rational Function (Precalculus - College Algebra 40)

Horizontal and Vertical Asymptotes - Slant / Oblique - Holes - Rational Function - Domain & Range

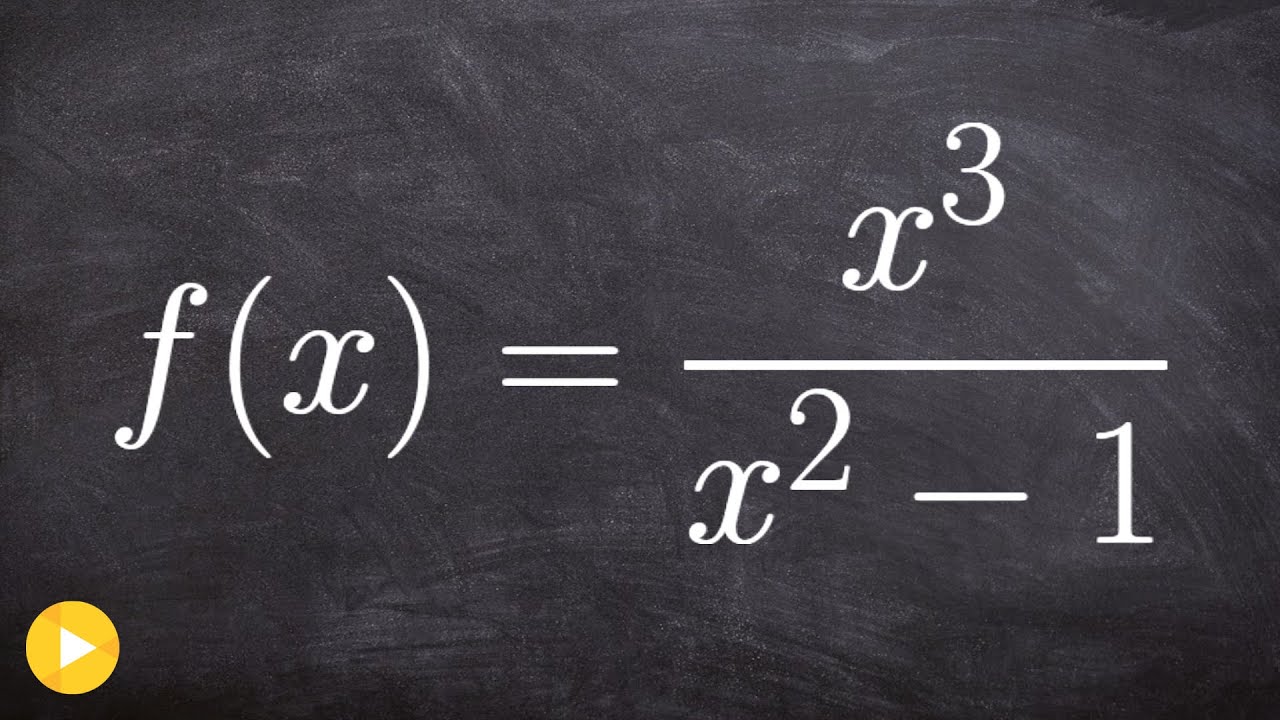
Finding the Slant Asymptote

Graphing Rational Functions and Their Asymptotes

Finding Asymptotes and Holes of Rational Functions (Precalculus - College Algebra 43)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Oblique AsymptotesRational FunctionsEnd BehaviorLong DivisionPolynomialsMath EducationDiagonal LinesInfinite LimitsFunction Analysis