Finding the Slant Asymptote

Brian McLogan
3 Nov 201105:25
EducationalLearning
32 Likes 10 Comments

TLDRThe video script offers a detailed tutorial on identifying vertical, horizontal, and slant asymptotes of a function. It starts by explaining how to find vertical asymptotes by determining the values of x that make the denominator zero, resulting in x = ±1 for the given example. The presenter then discusses horizontal asymptotes, emphasizing the importance of comparing the degrees of the leading terms of the numerator and denominator. If the degree of the numerator is greater, there is no horizontal asymptote, but a slant asymptote is present. The script demonstrates long division to find the slant asymptote, showing the process of dividing the polynomial by the divisor and highlighting the importance of the quotient in determining the asymptote. The tutorial concludes with a sketch of the graph to visualize where the graph will approach but not cross the asymptotes.

Takeaways
  • 📚 The video is a tutorial on how to find vertical, horizontal, and slant asymptotes of a function.
  • 📈 Vertical asymptotes occur at values of x that make the denominator of a rational function zero, as division by zero is undefined.
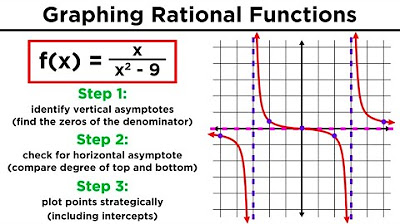
  • 🔍 To find vertical asymptotes, set the denominator equal to zero and solve for x, resulting in x = ±1 in this case.
  • 📊 The graph of the function will approach but never touch or cross the vertical asymptotes, which are at x = 1 and x = -1.
  • 📐 Horizontal asymptotes are determined by comparing the degrees of the polynomials in the numerator and denominator of the function.
  • ✂️ If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is at y = 0.
  • 🔄 If the degrees are equal, the horizontal asymptote is found by dividing the leading coefficient of the numerator by that of the denominator.
  • 🚫 If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote.
  • 💡 For functions without a horizontal asymptote, a slant (or oblique) asymptote may exist and is found using long division.
  • 📝 Long division is used to simplify the function into a form that can be analyzed for a slant asymptote, ensuring every term is accounted for in the division process.
  • 📉 The slant asymptote is the line that the function approaches but does not cross, which can be visualized without a table of values or graphing calculator.
Q & A

  • What is the main topic of the video script?

    -The main topic of the video script is how to find vertical, horizontal, and slant asymptotes of a function.

  • What are the vertical asymptotes in the context of the script?

    -Vertical asymptotes are the values of x for which the function approaches but never touches or crosses, typically occurring when x makes the denominator of a rational function zero.

  • How does one find the vertical asymptotes of a function?

    -To find the vertical asymptotes, set the denominator of the rational function to zero and solve for x, which will give the values that the graph approaches but never touches.

  • What is the significance of the degrees of the leading terms in determining horizontal asymptotes?

    -The degrees of the leading terms in the numerator and denominator of a rational function determine the behavior of the horizontal asymptote: if the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is y = 0; if they are equal, the horizontal asymptote is y = (leading coefficient of numerator) / (leading coefficient of denominator); if the degree of the numerator is greater, there is no horizontal asymptote.

  • How does the script differentiate between horizontal and slant asymptotes?

    -The script differentiates by comparing the degrees of the polynomials in the numerator and denominator. If the degree of the numerator is greater than the denominator, a slant asymptote is present instead of a horizontal one.

  • What is the method used to find the equation of a slant asymptote?

    -The method used to find the equation of a slant asymptote is long division, which helps to simplify the rational function and find the equation of the line that the graph approaches but never touches.

  • Why is long division preferred over synthetic division when finding slant asymptotes?

    -Long division is preferred because it does not require the function to be in factored form or to have a zero, which is necessary for synthetic division. It provides a direct method to find the slant asymptote.

  • What is the purpose of ensuring that every term is created during long division in the script?

    -Ensuring that every term is created, especially an x term, is necessary to avoid division by zero and to correctly perform the long division process to find the slant asymptote.

  • What does the script imply about the behavior of a graph approaching a slant asymptote?

    -The script implies that the graph of a function will approach the slant asymptote without ever crossing or touching it, similar to how it behaves with vertical asymptotes.

  • How can one sketch a graph without using a table of values or a graphing calculator, as suggested in the script?

    -One can sketch a graph by identifying where the graph will not touch or cross the asymptotes, using the information about vertical, horizontal, and slant asymptotes to guide the sketching process.

Outlines
00:00
📚 Finding Vertical and Horizontal Asymptotes

The speaker begins by explaining how to find vertical asymptotes (ASM tootes) in a function. They emphasize starting with the vertical lines, which are represented by values of X that the graph will approach but never touch or cross. For rational functions, vertical asymptotes occur where the denominator equals zero, as division by zero is undefined. The example given involves setting the bottom polynomial to zero, solving for X, and finding two vertical asymptotes at X = plus or minus 1. The speaker also briefly mentions the three rules for horizontal asymptotes but does not elaborate on them in this paragraph, suggesting viewers refer to other videos for more details.

05:01
📈 Determining Horizontal and Slant Asymptotes

In this paragraph, the focus shifts to horizontal and slant asymptotes. The speaker explains that the presence of a horizontal asymptote depends on the degrees of the leading terms of the numerator and denominator polynomials. If the degree of the numerator is less than the denominator, the horizontal asymptote is at y equals zero. If the degrees are equal, the horizontal asymptote is found by dividing the leading coefficients. However, if the numerator's degree is greater, there is no horizontal asymptote, and instead, a slant asymptote is present. To find the slant asymptote, long division is used, as it provides the quickest method to determine the line that the graph will approach but not cross. The speaker illustrates this with an example, showing the process of long division and emphasizing the importance of ensuring that every term is represented during the division.

Mindmap
Keywords
💡ASM tootes
ASM tootes, or Asymptotes, are lines that a graph approaches but never intersects. In the context of the video, the speaker is teaching how to find vertical, horizontal, and slant asymptotes of a function. Vertical asymptotes are values of x for which the function is undefined, while horizontal and slant asymptotes are lines that the graph approaches but never crosses.
💡Vertical Asymptotes
Vertical asymptotes are lines on the graph where the function approaches but never touches a certain value of x. They occur when the denominator of a rational function is zero, making the function undefined. The speaker explains that for vertical asymptotes, one must find values that make the bottom polynomial zero, resulting in x = ±1 in the given example.
💡Rational Function
A rational function is a function that is the ratio of two polynomials. The video script discusses finding asymptotes within the context of rational functions. The speaker mentions that values which make the bottom polynomial zero cannot be part of the function, as division by zero is undefined.
💡Horizontal Asymptotes
Horizontal asymptotes are horizontal lines that a graph approaches as x goes to infinity or negative infinity. The video explains that if the degree of the top polynomial is less than the degree of the bottom polynomial, the horizontal asymptote is at y = 0. If the degrees are equal, the horizontal asymptote is at y = the ratio of the leading coefficients.
💡Slant Asymptote
A slant or oblique asymptote is a diagonal line that a graph approaches as x goes to infinity or negative infinity. The video describes that a slant asymptote occurs when the degree of the top polynomial is greater than the degree of the bottom polynomial, and it is found using long division.
💡Long Division
Long division is a method used to divide polynomials. In the context of finding a slant asymptote, the speaker uses long division to divide the numerator polynomial by the denominator polynomial. The quotient of this division gives the equation of the slant asymptote, which the graph approaches but never touches.
💡Leading Term
The leading term of a polynomial is the term with the highest degree. In the video, the speaker explains that to determine horizontal asymptotes, one must consider the degrees of the leading terms of both the numerator and the denominator polynomials in a rational function.
💡Degrees of Polynomials
The degree of a polynomial is the highest power of the variable in the polynomial. In the script, the degrees of the polynomials are used to determine the presence and position of horizontal asymptotes. If the degree of the numerator is greater, there is no horizontal asymptote, but a slant asymptote is present.
💡Graph
A graph is a visual representation of a function, showing the relationship between variables. The video script discusses how to determine where a graph will not touch or cross certain lines (asymptotes) without using a graphing calculator or creating a table of values.
💡Sketch
A sketch in the context of the video refers to a rough drawing made to visualize the behavior of a function, particularly near its asymptotes. The speaker mentions sketching a graph to illustrate where the graph approaches but never touches the vertical asymptotes at x = ±1.
💡Polynomial
A polynomial is an expression consisting of variables and coefficients, involving only the operations of addition, subtraction, and multiplication, and non-negative integer exponents. The script discusses setting the bottom polynomial of a rational function to zero to find the values that cause the function to be undefined, which are the vertical asymptotes.
Highlights

Introduction to finding vertical, horizontal, and slant asymptotes.

Explanation of vertical asymptotes and their relation to values that do not hold true for x.

Vertical asymptotes occur where x values approach but never touch or cross.

Rational functions and the importance of not dividing by zero.

Finding vertical asymptotes by setting the bottom polynomial to zero.

Sketching a graph to illustrate vertical asymptotes.

Three rules for determining horizontal asymptotes.

Horizontal asymptotes when the degree of the top term is less than the bottom term.

Horizontal asymptotes when the degrees of the top and bottom terms are equal.

Absence of horizontal asymptotes when the degree of the top term is greater than the bottom term.

Introduction to slant asymptotes and their calculation using long division.

Long division as a method to find slant asymptotes.

Process of long division in the context of finding slant asymptotes.

Ensuring no zero x terms during long division.

Completing long division to find the slant asymptote.

Understanding the horizontal asymptote as the line the graph approaches but does not cross.

Conclusion on finding horizontal, slant, and vertical asymptotes without a graph or table of values.

Transcripts

Browse More Related Video

How to graph a rational function using 6 steps

Horizontal and Vertical Asymptotes - Slant / Oblique - Holes - Rational Function - Domain & Range

Finding a Horizontal Asymptote of a Rational Function (Precalculus - College Algebra 40)

Finding an Oblique Asymptote of a Rational Function (Precalculus - College Algebra 41)

Horizontal Asymptotes and Slant Asymptotes of Rational Functions

Graphing Rational Functions and Their Asymptotes

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
AsymptotesMath TutorialVertical AsymptotesHorizontal AsymptotesSlant AsymptotesRational FunctionsLong DivisionGraph AnalysisAlgebra LessonsEducational Content