Horizontal and Vertical Asymptotes - Slant / Oblique - Holes - Rational Function - Domain & Range

The Organic Chemistry Tutor

11 Aug 201631:35

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script offers a comprehensive guide to identifying the asymptotes of rational functions. It explains how to find vertical asymptotes by setting the denominator to zero and horizontal asymptotes by comparing the degrees of the numerator and denominator. The script also covers how to determine the domain and range of functions, as well as how to graph them, including the end behavior and intercepts. It delves into cases with no horizontal asymptote due to the numerator's degree exceeding the denominator's and introduces the concept of slant or oblique asymptotes, demonstrating the process with step-by-step examples and long division.

Takeaways

📚 To find the vertical asymptote of a rational function, set the denominator equal to zero and solve for x.
🌟 For a horizontal asymptote, determine if the function is 'top heavy', 'bottom heavy', or if the degrees of the numerator and denominator are equal. The horizontal asymptote is y=0 for bottom heavy functions, and y approaches the ratio of the leading coefficients for equal degrees.
📈 The end behavior of a function can be understood by looking at the horizontal asymptote, as the function approaches positive or negative infinity.
📉 The domain of a function is all possible x values excluding the vertical asymptote, and the range excludes the horizontal asymptote.
🔍 For rational functions where the degree of the numerator is higher than the denominator, there is no horizontal asymptote, and a slant or oblique asymptote exists.
📐 To find a slant or oblique asymptote, perform long division of the rational function and the result is the equation of the asymptote.
🔑 Factoring the numerator and denominator is crucial for identifying vertical asymptotes and holes in the graph of a rational function.
📊 Test points can be used to determine the position of the graph relative to the horizontal and vertical asymptotes.
📈 The graph of a rational function can be sketched by identifying intercepts, asymptotes, and using test points to understand the behavior on either side of discontinuities.
🔬 A hole in the graph, or point discontinuity, occurs when a factor in the numerator and denominator cancels out, but the vertical asymptote does not cancel.
📘 The domain and range of a function with a hole must exclude the x-coordinate of the hole and the vertical asymptote, and the range must also exclude the y-coordinate of the hole.

Q & A

What is a vertical asymptote and how do you find it?
-A vertical asymptote is a vertical line on the graph where the function approaches infinity or negative infinity as the input approaches a certain value. To find the vertical asymptote, set the denominator of the rational function equal to zero and solve for x.
How do you determine the horizontal asymptote of a rational function?
-To determine the horizontal asymptote, you need to check if the function is 'top heavy', 'bottom heavy', or if the degrees of the numerator and denominator are equal. If the degree of the denominator is higher, the horizontal asymptote is y=0. If they are equal, the horizontal asymptote is the ratio of the leading coefficients. If the numerator's degree is higher, there is no horizontal asymptote.
What is the domain of the function y = 1/(x - 3)?
-The domain of the function y = 1/(x - 3) is all real numbers except x = 3, since x = 3 makes the denominator zero and is the vertical asymptote. Therefore, the domain is (-∞, 3) union (3, ∞).
What is the range of the function y = 1/(x - 3)?
-The range of the function y = 1/(x - 3) is all real numbers except y = 0, because the function never touches the x-axis. Hence, the range is (-∞, 0) union (0, ∞).
How do you find the end behavior of a rational function?
-The end behavior of a rational function is determined by the horizontal asymptote. As x approaches positive infinity, the function approaches the value of the horizontal asymptote. Similarly, as x approaches negative infinity, the function also approaches the horizontal asymptote's value.
What is a slant or oblique asymptote?
-A slant or oblique asymptote is a diagonal line that the graph of a rational function approaches but never touches as x approaches infinity or negative infinity. It occurs when the degree of the numerator is exactly one more than the degree of the denominator.
How do you find the slant or oblique asymptote of a rational function?
-To find the slant or oblique asymptote, perform long division of the numerator by the denominator. The quotient from the division represents the equation of the slant asymptote.
What is a hole in the graph of a rational function?
-A hole is a point of discontinuity in the graph of a rational function where the x-coordinate of the hole is a common factor in both the numerator and the denominator that cancels out after simplification.
How do you find the x and y-intercepts of a rational function?
-To find the x-intercept, set y to zero and solve for x. To find the y-intercept, set x to zero and solve for y. These intercepts are points where the graph crosses or touches the x-axis and y-axis, respectively.
Can you provide an example of a rational function with a hole and describe its domain and range?
-An example of a rational function with a hole is y = (2x + 1)(x - 2) / (x + 3)(x - 2). The hole is at (2, 1). The domain excludes x = -3 and x = 2, so it is (-∞, -3) union (-3, 2) union (2, ∞). The range excludes y = 1 and y = 2, so it is (-∞, 1) union (1, 2) union (2, ∞).

Outlines

00:00

📚 Introduction to Asymptotes of Rational Functions

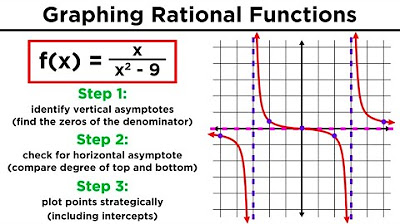
This paragraph introduces the topic of finding horizontal and vertical asymptotes of rational functions, as well as the concept of a slant or oblique asymptote if applicable. The first function, y = 1 / (x - 3), is used as an example. To find the vertical asymptote, the denominator is set to zero, resulting in x = 3. The horizontal asymptote is determined by comparing the degrees of the numerator and denominator, with this function being 'bottom heavy' and thus having a horizontal asymptote at y = 0. The function's graph, domain, range, and end behavior are also discussed, with the domain being all real numbers except x = 3 and the range being all real numbers except y = 0.

05:03

📈 Analyzing Asymptotes with Additional Terms

The second paragraph discusses the function y = 1 / (x + 2) + 7. The vertical asymptote is found by setting the denominator to zero, resulting in x = -2. The horizontal asymptote is influenced by the additional +7 term, shifting the asymptote up seven units to y = 7. Test points are used to illustrate the graph's behavior on either side of the vertical asymptote, confirming the function's position relative to the horizontal asymptote. The domain and range are also explained, with the domain being all real numbers except x = -2 and the range excluding y = 7.

10:05

🔍 Horizontal Asymptote Calculation with Equal Degrees

The third paragraph examines the function y = (6x - 18) / (2x + 4), where the degrees of the numerator and denominator are equal. The horizontal asymptote is determined by ignoring the constant terms, resulting in y = 3 as x approaches infinity. The vertical asymptote is found by setting the denominator to zero, yielding x = -2. The x-intercept and y-intercept are calculated, and the function's graph is sketched, including the intercepts and asymptotes. The domain is all real numbers except x = -2, and the range excludes y = 3.

15:06

📘 Factoring to Determine Asymptotes and Graph

In the fourth paragraph, the function y = (2x^2 - 3x - 2) / (x^2 + x - 6) is explored. The horizontal asymptote is determined by comparing coefficients, resulting in y = 2. The vertical asymptote is found by factoring the denominator and solving for x, which gives x = -3. The numerator is also factored to check for a hole in the graph, which is not present. The y-coordinate of the hole is calculated, and the function's graph is sketched with the vertical asymptote, horizontal asymptote, and the point of discontinuity. The domain excludes x = -3 and x = 2, while the range excludes y = 1 and y = 2.

20:06

📊 Graphing Functions with Slant Asymptotes

The fifth paragraph focuses on the function y = (2x^2 - x + 1) / (x - 2), which has a vertical asymptote at x = 2 and no horizontal asymptote due to the top-heavy nature of the function. A slant or oblique asymptote is determined using long division, resulting in the equation y = 2x + 3. The function is graphed with the vertical asymptote and the slant asymptote, which acts as a guide for the function's end behavior. The domain excludes x = 2, and the range excludes y values between the horizontal asymptote and the y-coordinate of the hole.

25:08

🎓 Conclusion and Final Function Analysis

The final paragraph wraps up the video with a last example, y = (2x^2 - x + 1) / (x - 2), reinforcing the concepts of vertical and slant asymptotes. The vertical asymptote is at x = 2, and the slant asymptote is y = 2x + 3. Two points are calculated to illustrate the function's behavior on either side of the vertical asymptote. The graph is sketched, showing the function's position relative to the slant asymptote. The video concludes with a reminder of the importance of understanding asymptotes for graphing rational functions.

Mindmap

Keywords

💡Asymptote

An asymptote is a line that a function approaches but never touches. In the context of the video, the focus is on finding horizontal and vertical asymptotes of rational functions. Horizontal asymptotes are used to determine the end behavior of a function as x approaches infinity or negative infinity, while vertical asymptotes are found by setting the denominator of a rational function to zero. For example, the script discusses finding the vertical asymptote of the function y = 1 / (x - 3) by setting x - 3 to zero, resulting in x = 3.

💡Rational Function

A rational function is a mathematical function that is the ratio of two polynomials. The video's theme revolves around analyzing rational functions to find their asymptotes. The script provides several examples of rational functions, such as y = 1 / (x - 3), and demonstrates how to determine their vertical and horizontal asymptotes.

💡Vertical Asymptote

A vertical asymptote is a line that the graph of a function approaches but never crosses as the input (x-value) approaches a certain value. The video script explains that to find a vertical asymptote, one must set the denominator of a rational function to zero and solve for x, as demonstrated with the function y = 1 / (x - 3), where x - 3 = 0 leads to the vertical asymptote x = 3.

💡Horizontal Asymptote

A horizontal asymptote is a horizontal line that indicates the limit of a function's growth or decay as the independent variable (x) approaches infinity or negative infinity. The video script explains that horizontal asymptotes are determined by comparing the degrees of the numerator and denominator of a rational function. For instance, if the degree of the denominator is higher, as in y = 1 / (x - 3), the horizontal asymptote is y = 0.

💡Degree of a Polynomial

The degree of a polynomial is the highest power of x in the polynomial. In the video, the degree of the numerator and denominator is used to determine the horizontal asymptote of a rational function. If the degree of the numerator is higher than the denominator, there is no horizontal asymptote, as explained for the function y = (2x^2 - x + 1) / (x - 2).

💡Slant Asymptote

A slant or oblique asymptote is a line that the graph of a function approaches but never touches, which is not horizontal or vertical. The video script explains that a slant asymptote occurs when the degree of the numerator is exactly one more than the degree of the denominator. The script demonstrates finding a slant asymptote for the function y = (2x^2 - x + 1) / (x - 2) using long division.

💡Long Division

Long division is a method used to divide a polynomial by another polynomial. In the context of the video, long division is used to find the slant asymptote of a rational function when the degree of the numerator is one more than the degree of the denominator. The script shows the process of long division for the function y = (2x^2 - x + 1) / (x - 2) to find the slant asymptote y = 2x + 3.

💡Domain

The domain of a function is the set of all possible input values (x-values) for which the function is defined. The video script explains how to determine the domain of a function by removing the x-values that cause the denominator to be zero, which would create a vertical asymptote. For example, the domain of y = 1 / (x - 3) is all real numbers except x = 3.

💡Range

The range of a function is the set of all possible output values (y-values) that result from the input values in the domain. The video script discusses how to find the range by considering the horizontal asymptote and ensuring that the function does not touch it. For instance, the range of y = 1 / (x - 3) is all real numbers except y = 0, as the function never touches the horizontal asymptote y = 0.

💡Factoring

Factoring is the process of breaking down a polynomial into a product of other polynomials. In the video, factoring is used to simplify rational functions and to find vertical asymptotes. The script demonstrates factoring the numerator and denominator of the function y = (6x - 18) / (2x + 4) to find the vertical asymptote x = -2.

💡End Behavior

End behavior refers to the behavior of a function as the input (x-value) approaches very large positive or negative values. The video script explains how to determine the end behavior of a function by considering the horizontal asymptote. For example, for the function y = 1 / (x - 3), as x approaches positive infinity, y approaches zero, which is the horizontal asymptote.

Highlights

Finding horizontal and vertical asymptotes of a rational function is the main focus of the video.

Slant or oblique asymptotes are also discussed if present in the function.

Vertical asymptote is found by setting the denominator equal to zero.

Horizontal asymptote for a 'bottom heavy' function is y equals zero.

For 'top heavy' functions, there is no horizontal asymptote.

Degree of the denominator higher than the numerator indicates a 'bottom heavy' function.

Graphing rational functions involves identifying asymptotes and test points.

Domain of a function excludes the vertical asymptote.

Range of a function excludes the horizontal asymptote.

End behavior of a function is often the horizontal asymptote.

Horizontal asymptote is determined by comparing degrees of numerator and denominator.

For functions with the same degree in numerator and denominator, the horizontal asymptote is the ratio of leading coefficients.

Factoring the numerator and denominator is necessary to find vertical asymptotes.

X-intercepts are found by setting the numerator equal to zero.

Y-intercepts are found by setting x to zero and solving for y.

Oblique or slant asymptotes occur when the degree of the numerator exceeds that of the denominator by one.

Long division is used to find the equation of a slant asymptote.

The presence of a hole in a function affects the domain and range calculations.

Graphing a function with a slant asymptote involves sketching the asymptote and determining the function's behavior around it.

Transcripts

Browse More Related Video

Horizontal Asymptotes and Slant Asymptotes of Rational Functions

Finding an Oblique Asymptote of a Rational Function (Precalculus - College Algebra 41)

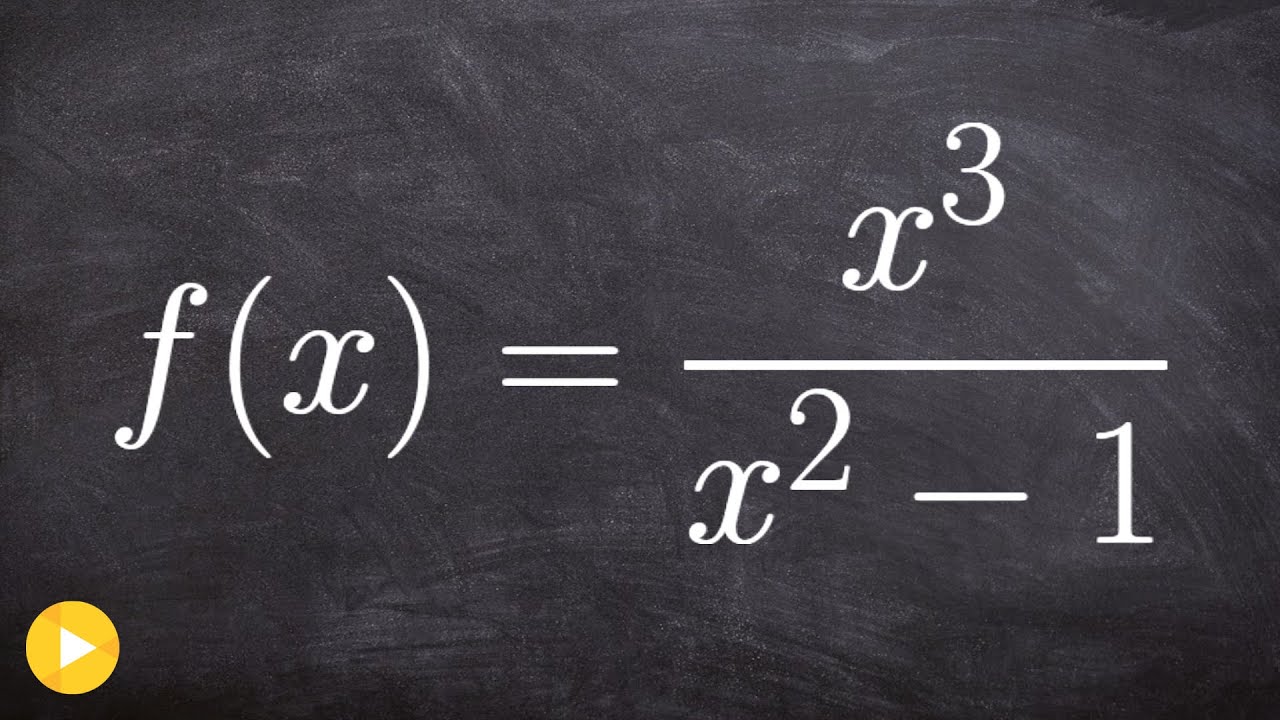
Finding the Slant Asymptote

Graphing Rational Functions and Their Asymptotes

Finding a Horizontal Asymptote of a Rational Function (Precalculus - College Algebra 40)

How to graph a rational function using 6 steps

Related Tags

Asymptote Calculation Rational Functions Math Education Vertical Asymptote Horizontal Asymptote Slant Asymptote Graphing Functions Algebra Tutorial Math Concepts Educational Video