Horizontal Asymptotes and Slant Asymptotes of Rational Functions

The Organic Chemistry Tutor
24 Jan 201810:49
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script focuses on identifying horizontal and slant (oblique) asymptotes in mathematical functions. It explains that horizontal asymptotes occur when the degree of the denominator exceeds the numerator, leading to y=0, or when the degrees are equal, resulting in the ratio of leading coefficients. Slant asymptotes are found when the numerator's degree is exactly one more than the denominator's, using polynomial long division to determine the asymptote equation. The script provides several examples to illustrate these concepts and encourages viewers to practice identifying asymptotes in given functions.

Takeaways
  • 📐 Horizontal asymptotes occur when the degree of the denominator is greater than or equal to the numerator.
  • ➗ For bottom-heavy functions, the horizontal asymptote is y = 0.
  • 📉 If the degree of the numerator is higher than the denominator by exactly one, there is a slant asymptote.
  • ✏️ Example: For the function 1/x, the horizontal asymptote is y = 0 because the denominator's degree is greater.
  • 🧮 In functions like 7/(x-3), the horizontal asymptote remains y = 0 for bottom-heavy cases.
  • ➕ Adding a constant to a bottom-heavy function shifts the horizontal asymptote by that constant value.
  • ⚖️ When the numerator and denominator degrees are equal, divide their coefficients for the horizontal asymptote.
  • 🔀 Example: For 2x/(x+4), the horizontal asymptote is y = 2 because the degrees are equal and 2/1 = 2.
  • 📝 When the numerator's degree exceeds the denominator's by exactly one, use long division to find the slant asymptote.
  • 🔎 Functions like 5x^4 - 6x + 2 / (7x - 3) with a numerator degree much higher have no horizontal or slant asymptotes.
Q & A

  • What is a horizontal asymptote?

    -A horizontal asymptote is a horizontal line that a function approaches as its input (x-values) approaches either positive or negative infinity. It represents the end behavior of the function.

  • How do you determine if a function has a horizontal asymptote?

    -You determine a horizontal asymptote by comparing the degrees of the numerator and denominator of the rational function. If the degree of the denominator is greater than the degree of the numerator, the horizontal asymptote is y = 0. If the degrees are the same, the horizontal asymptote is the ratio of the leading coefficients. If the degree of the numerator is greater, there is no horizontal asymptote.

  • What is the horizontal asymptote of the function 1/x?

    -The horizontal asymptote of the function 1/x is y = 0 because the degree of the denominator (x) is greater than the degree of the numerator (1), making it a 'bottom heavy' function.

  • What is the horizontal asymptote for a function where the degree of the numerator is one and the degree of the denominator is also one?

    -In such a case, the horizontal asymptote is determined by dividing the leading coefficient of the numerator by that of the denominator. For example, for the function (2x - 3) / (x + 4), the horizontal asymptote is y = 2/1 = 2.

  • What is a slant or oblique asymptote?

    -A slant or oblique asymptote is a line that a function approaches as its input (x-values) approaches either positive or negative infinity, but unlike a horizontal asymptote, it is not horizontal. It occurs when the degree of the numerator is exactly one more than the degree of the denominator.

  • How do you find the slant asymptote of a function?

    -To find the slant asymptote, you perform polynomial long division of the numerator by the denominator. The quotient from this division gives you the equation of the slant asymptote.

  • What is the slant asymptote of the function x^2 + 5x + 6 divided by x + 3?

    -The slant asymptote of the function x^2 + 5x + 6 / (x + 3) is y = x + 2, which is found by dividing x^2 by x to get x, then subtracting and continuing the division process until there is no remainder.

  • Can a function have both a horizontal and a slant asymptote?

    -No, a function cannot have both a horizontal and a slant asymptote. A slant asymptote occurs when the degree of the numerator is exactly one more than the denominator, which would not allow for a horizontal asymptote.

  • What happens when the degree of the numerator exceeds the denominator by more than one?

    -When the degree of the numerator exceeds the degree of the denominator by more than one, there is no slant or oblique asymptote. The function will not approach a linear function as x approaches infinity.

  • What is the horizontal asymptote of the function 5/(x + 2) + 3?

    -The horizontal asymptote of the function 5/(x + 2) + 3 is y = 3. This is because the function is 'bottom heavy' with a horizontal asymptote of y = 0 for 5/(x + 2), and adding 3 to this gives y = 3.

Outlines
00:00
📚 Identifying Horizontal and Slant Asymptotes

This paragraph explains how to identify horizontal and slant (oblique) asymptotes in functions. It starts with the example of 1/x, which has a horizontal asymptote at y=0 due to the 'bottom heavy' nature where the degree of the denominator is greater than the numerator. The concept is applied to various examples, showing that when the degree of the numerator is equal to the denominator, the horizontal asymptote is found by dividing the leading coefficients. For functions where the numerator's degree exceeds the denominator by exactly one, a slant asymptote exists, which can be found using long division. If the degree exceeds by more than one, there is no slant asymptote.

05:01
🔍 Detailed Process of Finding Slant Asymptotes

This paragraph delves into the process of finding slant asymptotes through long division. It uses the example of dividing x^2 + 5x + 6 by x + 3, showing each step of the division and explaining how to arrive at the slant asymptote equation y = x + 2. The paragraph also discusses another example with 2x^3 - 8x + 6 divided by x^2 + 4, illustrating that a slant asymptote exists when the degree of the numerator exceeds the denominator by one. The division process is shown, and the slant asymptote is identified as y = 2x. It concludes by emphasizing that a slant asymptote is only possible when the degree difference is exactly one.

10:01
📘 Practice Problems for Asymptote Identification

The final paragraph presents practice problems for viewers to apply the concepts learned about horizontal and slant asymptotes. It provides examples with varying degrees of complexity, including functions that are 'bottom heavy' with horizontal asymptotes at y=0, and others where the horizontal asymptote is determined by dividing the leading coefficients. The paragraph also includes a function with a slant asymptote, where the degree of the numerator is exactly one more than the denominator, and a case where there is no asymptote due to the degree difference being more than one. The aim is to reinforce the understanding of asymptote identification through practice.

Mindmap
Keywords
💡Horizontal Asymptote
A horizontal asymptote is a horizontal line that a function approaches as its input (or the variable) approaches infinity or negative infinity. In the context of the video, it is a key concept used to describe the behavior of rational functions. The script explains that if the degree of the denominator is greater than the degree of the numerator, the horizontal asymptote is y = 0, as seen in the function 1/x where the degree of the denominator (x) is higher than the numerator (constant).
💡Slant Asymptote
A slant or oblique asymptote is a diagonal line that a function approaches as the input becomes very large or very small. The video discusses this concept in relation to rational functions where the degree of the numerator exceeds the degree of the denominator by exactly one. An example given is the function (x^2 + 5x + 6) / (x + 3), which after long division, results in a slant asymptote of y = x + 2.
💡Degree of a Polynomial
The degree of a polynomial is the highest power of the variable in the polynomial expression. In the video, determining the degree of the numerator and the denominator is crucial for identifying horizontal and slant asymptotes. For instance, if the degree of the numerator is one more than the degree of the denominator, a slant asymptote exists.
💡Bottom Heavy Function
A bottom heavy function refers to a rational function where the degree of the denominator is greater than the degree of the numerator. The video script uses this term to describe functions that have a horizontal asymptote at y = 0, such as 7/(x - 3), where the degree of the denominator (x - 3) is one, and the degree of the numerator (7) is zero.
💡Top Heavy Function
Conversely, a top heavy function is one where the degree of the numerator exceeds that of the denominator. The script mentions that if the degree of the numerator is more than one greater than the degree of the denominator, there is no horizontal or slant asymptote, as seen in the function (5x^4 - 6x + 2) / (7x - 3).
💡Long Division
Long division is a method used to divide a polynomial by another polynomial. It is essential for finding slant asymptotes, as demonstrated in the video when dividing (x^2 + 5x + 6) by (x + 3). The quotient of this division represents the equation of the slant asymptote, y = x + 2.
💡Coefficients
Coefficients are the numerical factors that multiply the variables in a polynomial. In the video, when the degrees of the numerator and denominator are the same, the horizontal asymptote is determined by dividing the leading coefficients, such as in the function (12x - 6) / (3x + 4) where the horizontal asymptote is y = 6.
💡Remainder
In the context of polynomial long division, the remainder is what is left over after the division process. The script explains that for determining slant asymptotes, the remainder is not considered, as the asymptote is represented by the quotient, such as in the division of 2x^3 - 8x + 6 by x^2 + 4, where the slant asymptote is y = 2x.
💡Practice Problems
Practice problems are exercises provided at the end of the video script for viewers to apply the concepts learned. They are designed to reinforce understanding of horizontal and slant asymptotes. For example, one practice problem involves determining the horizontal asymptote of a function with the highest degree term x^2 on top and a coefficient of two, resulting in a horizontal asymptote of y = -2/5.
💡Dividing Coefficients
Dividing coefficients is a method used to find the horizontal asymptote when the degrees of the numerator and denominator polynomials are equal. The video script illustrates this with the function (8x - 6) / (x^2 + 3x), where the horizontal asymptote is determined by dividing the coefficients of the highest degree terms, resulting in y = 5.
Highlights

Introduction to identifying horizontal and slant (oblique) asymptotes.

Explanation of horizontal asymptote for functions with a 'bottom-heavy' structure where the degree of the denominator is higher than the numerator.

Horizontal asymptote is y=0 when the degree of the denominator is one and the numerator is a constant.

Example of identifying horizontal asymptote for 7/(x-3), emphasizing the bottom-heavy nature leading to y=0.

Adjusting horizontal asymptote by adding constants outside the fraction, as shown with 5/(x+2)+3 leading to y=3.

Identifying horizontal asymptote for functions with a higher degree in the numerator than the denominator, like 8x-6/x^2+3x, resulting in y=0.

Adjusting horizontal asymptote by subtracting constants, as in 8x-6/x^2+3x - 9 leading to y=-9.

Method for finding horizontal asymptote when the degree of numerator and denominator are equal, by dividing coefficients.

Example of horizontal asymptote calculation with 12x-6/3x+4+2, resulting in y=6.

Procedure for finding horizontal asymptote when degrees are the same, illustrated with 5-8x^2/2x^2+5-5.

Explanation of no horizontal asymptote for 'top-heavy' functions where the numerator's degree exceeds the denominator's.

Introduction to slant (oblique) asymptotes for functions where the numerator's degree exceeds the denominator's by exactly one.

Technique for finding slant asymptotes using long division, demonstrated with x^2+5x+6/x+3.

Result of slant asymptote calculation, showing y=x+2 for the given example.

Example of finding slant asymptote for 2x^3-8x+6/x^2+4, emphasizing the division process.

Explanation that no slant asymptote exists when the numerator's degree exceeds the denominator's by more than one.

Practice problems provided for determining horizontal and slant asymptotes.

Solution to a practice problem involving horizontal asymptote calculation with coefficients and constants.

Guidance on working through practice problems to reinforce understanding of asymptote identification.

Transcripts

Browse More Related Video

Finding a Horizontal Asymptote of a Rational Function (Precalculus - College Algebra 40)

Finding an Oblique Asymptote of a Rational Function (Precalculus - College Algebra 41)

Horizontal and Vertical Asymptotes - Slant / Oblique - Holes - Rational Function - Domain & Range

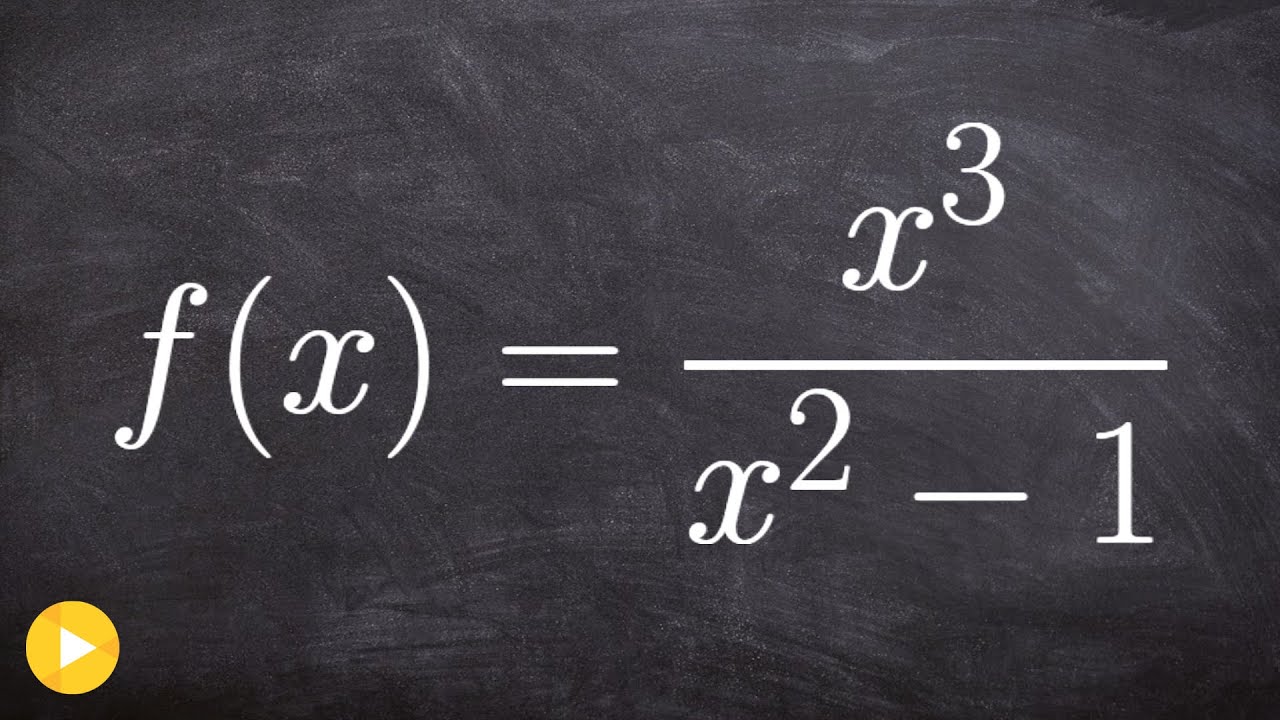
Finding the Slant Asymptote

How to graph a rational function using 6 steps

Graphing Rational Functions and Their Asymptotes

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Asymptote AnalysisMathematicsEducationalGraphingAlgebraCalculusHorizontal AsymptoteSlant AsymptoteOblique AsymptoteLong Division