Cramer's Rule - 3x3 Linear System

The Organic Chemistry Tutor
19 Feb 201815:02
EducationalLearning
32 Likes 10 Comments

TLDRThis tutorial demonstrates how to apply Kramer's Rule to solve a system of linear equations with three variables. The process involves calculating determinants to find the values of x, y, and z for the given equations. By following the step-by-step explanation, users learn how to evaluate a 3x3 determinant and use it to find the solution: x=1, y=2, z=3.

Takeaways
  • 📝 The tutorial covers the use of Kramer's Rule to solve a system of linear equations with three variables.
  • 🔢 The system of equations is represented in the form of ax + by + cz = d, with coefficients and variables indicated by their respective subscripts.
  • 🌟 The determinant (denoted as D) is a key component in solving the system, calculated from a 3x3 matrix composed of the coefficients of the variables.
  • 📊 To calculate D, you evaluate a 3x3 determinant by following a specific pattern of alternating signs and nested 2x2 determinants.
  • 🔍 The values for the determinant a1, b1, and c1 are derived from the original system of equations and are used to calculate the determinants.
  • 📈 The process of finding the determinant involves eliminating specific rows and columns to simplify the matrix and compute the values.
  • 👉 The solutions for x, y, and z are obtained by calculating the values of dx, dy, and dz, which are then divided by the determinant D.
  • 🧩 The values of dx, dy, and dz are determined by replacing the coefficients of the variable of interest with the constants from the equations and calculating the determinants.
  • 🔎 The solution to the system is expressed as an ordered set (x, y, z), with each variable's value resulting from the division of its corresponding determinant by the overall determinant D.
  • 🎓 Kramer's Rule is a powerful tool for solving systems of linear equations, providing a clear and methodical approach to finding the values of the variables involved.
Q & A

  • What is the main topic of the tutorial?

    -The main topic of the tutorial is how to use Kramer's Rule to solve a system of linear equations with three variables.

  • What are the three equations given in the example?

    -The three equations given are: 2x + y - z = 1, 3x + 2y + 2z = 13, and 4x - 2y + 3z = 9.

  • What does the determinant 'd' represent in the context of the tutorial?

    -In the context of the tutorial, 'd' represents the determinant of the coefficient matrix for the system of equations.

  • How is the determinant 'a1' calculated?

    -The determinant 'a1' is calculated by eliminating the row and column corresponding to the element 'a1' and then finding the determinant of the remaining 2x2 matrix.

  • What is the value of 'd' calculated in the example?

    -The value of 'd' calculated in the example is 33.

  • What are 'dx', 'dy', and 'dz' in the context of Kramer's Rule?

    -'dx', 'dy', and 'dz' are the determinants that correspond to the coefficients in front of x, y, and z when the constant term is replaced with the determinant 'd' in the system of equations.

  • What is the value of 'dx' in the example?

    -The value of 'dx' in the example is 33.

  • What is the value of 'dy' in the example?

    -The value of 'dy' in the example is 66.

  • What is the value of 'dz' in the example?

    -The value of 'dz' in the example is 99.

  • What is the solution to the system of equations in the example?

    -The solution to the system of equations in the example is x = 1, y = 2, and z = 3.

  • How does Kramer's Rule help in solving a system of linear equations?

    -Kramer's Rule provides a method to solve a system of linear equations by calculating determinants and using them to find the values of the variables. It is particularly useful for systems with three variables, as shown in the tutorial.

  • What is the significance of the determinant 'd' being non-zero in using Kramer's Rule?

    -The determinant 'd' being non-zero is significant because it indicates that the system of equations has a unique solution. If 'd' were zero, it would suggest that the system is either inconsistent or dependent, meaning there are no solutions or an infinite number of solutions, respectively.

Outlines
00:00
📚 Introduction to Kramer's Rule

This paragraph introduces the concept of Kramer's Rule, a method used to solve a system of linear equations with three variables. The paragraph presents an example of such a system, detailing the equations and their components. It explains the general form of the equations, the representation of coefficients, and the subscripts that indicate the row. The paragraph also outlines the initial steps in calculating the determinant (denoted as 'd') necessary for solving the system using Kramer's Rule. The process of evaluating a 3x3 determinant is described, including the elimination of rows and columns to simplify the matrix and calculate the determinant's value.

05:02
🔢 Calculation of Determinant 'd'

In this paragraph, the process of calculating the determinant 'd' for the given system of equations is detailed. It begins by explaining the elements of the 3x3 determinant matrix and the method for evaluating it. The paragraph then walks through the calculation, demonstrating how to eliminate specific rows and columns to simplify the matrix and compute the determinant. The final result of the determinant 'd' is found to be 33 after performing the necessary arithmetic operations on the elements of the matrix.

10:05
📈 Solving for 'x', 'y', and 'z' using Kramer's Rule

The final paragraph focuses on using Kramer's Rule to solve for the variables 'x', 'y', and 'z' in the system of equations. It explains the process of calculating the determinants for each variable (dx, dy, and dz) and how to use these in finding the values of the variables. The paragraph provides a step-by-step breakdown of the calculations, including the elimination of rows and columns and the arithmetic operations required. The solutions for 'x', 'y', and 'z' are found to be 1, 2, and 3, respectively. The paragraph concludes by summarizing the entire process and emphasizing the successful application of Kramer's Rule to solve the system of equations.

Mindmap
Keywords
💡Kramer's Rule
Kramer's Rule is a method used to solve a system of linear equations with three variables. It is a specific case of Cramer's Rule, which is applicable when the determinant of the coefficient matrix is non-zero. In the video, Kramer's Rule is used to find the values of x, y, and z for the given system of equations. The rule states that each variable can be expressed as the quotient of two determinants, where one determinant is the coefficient matrix with the corresponding column replaced by the constants from the equations.
💡Linear Equations
Linear equations are mathematical equations in which the highest power of the variables is one. They are used to represent relationships between different variables that are proportional to each other. In the context of this video, a system of linear equations with three variables (x, y, z) is given, and the goal is to find the values of these variables that satisfy all equations simultaneously.
💡Coefficients
Coefficients are numerical factors that are multiplied by variables in a linear equation. They indicate the relative contribution or weight of each variable in the equation. In the video, the coefficients are the numbers in front of the variables x, y, and z in the system of equations, which are used to build the determinants needed for solving the system using Kramer's Rule.
💡Determinant
A determinant is a scalar value that can be computed from the elements of a square matrix and is used in various areas of mathematics, including linear algebra. In the context of the video, the determinant is used to find the inverse of a matrix and to solve systems of linear equations using Cramer's Rule. A determinant of a matrix is zero if the matrix is singular and cannot be inverted, which indicates that the system of equations may be dependent or inconsistent.
💡Matrix
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. In linear algebra, matrices are used to represent systems of linear equations, where each column typically represents a variable and each row represents an equation. The video script describes how to use matrices to apply Kramer's Rule and solve the system of equations.
💡Variables
Variables are symbols, often letters, that represent unknown quantities or values that can change within an equation or a mathematical model. In the context of the video, the variables are x, y, and z, which are the unknowns being solved for in the system of linear equations.
💡Cramer's Rule
Cramer's Rule is a general method for solving a system of linear equations with as many variables as there are equations, provided that the determinant of the coefficient matrix is non-zero. It expresses each variable as the quotient of two determinants, one including the coefficients of the variables and the other including the constants from the equations. The rule is particularly useful when dealing with systems of linear equations with three or more variables, as it provides a straightforward way to find the solution without needing to manipulate or reduce the system.
💡System of Equations
A system of equations is a collection of mathematical equations that are often related to each other and need to be solved simultaneously. Each equation in the system represents a condition or constraint on the variables involved. In the context of the video, the system of equations consists of three linear equations with three variables, which must be solved to find the values of the variables that satisfy all equations at once.
💡Solving Equations
Solving equations refers to the process of finding the values of the variables that make the equations true. In the context of this video, solving equations involves using a specific method, Kramer's Rule, to find the values of x, y, and z that satisfy the given system of linear equations with three variables.
💡Constants
Constants are fixed values that do not change in a mathematical equation or system of equations. In the context of the video, the constants are the numbers on the right side of the equations in the system, which are used in conjunction with the coefficients and variables to form the system and are part of the determinant calculations required for solving the system using Kramer's Rule.
💡Subscripts
Subscripts are characters or numbers placed below and to the right of a line of text to indicate a particular element within a sequence or set. In the context of the video, subscripts are used to denote the row numbers in the matrix representation of the system of linear equations, helping to distinguish between different coefficients and variables in the equations.
Highlights

Introduction to Kramer's Rule for solving a system of linear equations with three variables.

Equation system representation: a1x + b1y + c1z = d1, a2x + b2y + c2z = d2, a3x + b3y + c3z = d3.

Explanation of coefficients and subscripts representing the rows in the equation system.

Solution approach: x = dx/d, y = dy/d, z = dz/d.

Step-by-step guide on evaluating a 3x3 determinant for calculating 'd'.

Elaboration on how to find a1, a2, a3, b1, b2, b3, c1, c2, c3 using matrix elimination.

Calculation of determinant 'd' with the given coefficients resulting in d = 33.

Process of calculating dx, the determinant for the x variable, resulting in dx = 33.

Explanation for calculating dy, the determinant for the y variable, which results in dy = 66.

Procedure for finding dz, the determinant for the z variable, with dz = 99.

Final solution derivation: x = 1, y = 2, z = 3.

Practical application of Kramer's Rule in solving a system of equations with three variables.

Emphasis on the importance of understanding matrix determinants for applying Kramer's Rule.

Demonstration of the method for eliminating variables to find the determinants a1, a2, a3, b1, b2, b3, c1, c2, c3.

Detailed explanation of how to perform the calculations for each determinant in the equation system.

The significance of the determinant 'd' in finding the unique solution to the system of equations.

Clear and concise presentation of the mathematical process, making it accessible for learning and understanding.

Transcripts

Browse More Related Video

Cramer's Rule - 2x2 & 3x3 Matrices - Solving Systems of Linear Equations - 2 & 3 Variables

PreCalculus - Matrices & Matrix Applications (33 of 33) Using Cramer's Rule to Find x=? y=? z=?

Solve a system of three variables

Cramer's Rule - 2x2 Linear System

Solving 3 Equations for 3 Unknowns Using a Matrix in Row Echelon Form

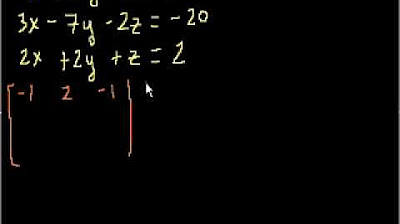
Solving 3 Equations with 3 Unknowns

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Kramer's RuleLinear EquationsMathematicsEducational TutorialVariable SystemDeterminant CalculationEquation SolvingMath CoachingAlgebra TechniquesNumerical Analysis