Solve a system of three variables

Brian McLogan
11 Oct 201212:45
EducationalLearning
32 Likes 10 Comments

TLDRThe transcript details a step-by-step process for solving a system of three-variable linear equations using elimination. The speaker instructs the audience to reduce the system to a two-variable system by eliminating the easiest variable, in this case, 'z'. Through a series of calculations, the speaker arrives at a new two-variable system and proceeds to eliminate 'y' to find 'x'. Despite a minor mistake, the speaker corrects it and eventually finds the values for 'x', 'y', and 'z', concluding with the solution: x = -1, y = 3, and z = -1.

Takeaways
  • 📝 The lecture focuses on solving systems of equations with three variables, emphasizing the importance of reducing the system to a two-variable system for easier resolution.
  • 🎯 When dealing with three-variable systems, the goal is to eliminate one variable, preferably one with a coefficient of one or negative one, to simplify the equations.
  • 📊 Two main methods for solving two-variable systems are mentioned: elimination and substitution, as well as graphing.
  • 🔢 The process begins by selecting two equations to eliminate the chosen variable; the lecture demonstrates this using equations labeled as number one and two, and two and three.
  • 🔍 The elimination technique is applied by multiplying one of the equations by a factor that creates a coefficient of the variable to be eliminated that can be easily canceled out when adding the equations.
  • ✍️ The lecturer provides a step-by-step example of eliminating the variable 'z' by multiplying the second equation by three and adding it to the first, resulting in a new two-variable equation.
  • 📌 After eliminating 'z', the lecturer is left with two new equations (labeled as 'a' and 'b') with only 'x' and 'y' variables.
  • 📐 The next step is to use the elimination method again on the two-variable equations to find the value of one variable, which in this case, the lecturer chooses to eliminate 'y'.
  • 🤔 The lecturer multiplies equation 'a' by -5 and equation 'b' by 2 to make the coefficients of 'y' opposites, allowing for easy elimination.
  • 👌 By adding the modified equations 'a' and 'b', the讲师 finds the value of 'x' to be -1, which is then substituted back into one of the original equations to find the value of 'y'.
  • 🔚 Finally, with the values of 'x' and 'y' known, the讲师 solves for 'z' and presents the complete solution to the system of equations as x = -1, y = 3, and z = -1.
Q & A

  • What is the main goal when dealing with a system of equations with three variables?

    -The main goal is to reduce the system to a system of two equations with two variables.

  • What are the three different processes learned for solving systems of equations with two variables?

    -The three processes are elimination, substitution, and graphing.

  • Which variable is considered the best to eliminate first in the system of equations?

    -The best variable to eliminate first is the one with a coefficient of one or negative one.

  • How does the speaker choose which equations to use for eliminating the variable z?

    -The speaker chooses equations 1 and 2, and later equations 2 and 3, because they have coefficients that can be easily manipulated to eliminate the z variable.

  • What is the process of eliminating the z variable in the given example?

    -The process involves multiplying equation 2 by 3 and then adding it to equation 1 to create a new equation with only x and y variables.

  • What method is used to solve the resulting system of two-variable equations?

    -The elimination method is used to solve the system of two-variable equations.

  • How does the speaker decide which variable to eliminate in the two-variable equations?

    -The speaker decides to eliminate the y variable because it is easier to do so with the coefficients available in the new equations.

  • What are the final values of x, y, and z after solving the system of equations?

    -The final solution is x equals negative one, y equals 3, and z equals negative one.

  • What mistake does the speaker make while solving the problem?

    -The speaker initially makes a mistake in the calculation when plugging the values of x and y back into the equation to solve for z, but corrects it after re-evaluating the work.

  • How does the speaker address the mistake made during the problem-solving process?

    -The speaker acknowledges the mistake and corrects it by re-evaluating the calculations and confirming the correct values of the variables.

  • What advice does the speaker give for solving problems like this?

    -The speaker advises that there are multiple ways to approach the problem and that it is easy to make mistakes, so careful checking and verification of the work are important.

Outlines
00:00
📝 Introduction to Solving Systems of Equations

The speaker begins by addressing the audience and acknowledges that homework quizzes have been taken away. They suggest writing down the process for solving systems of equations with three variables, emphasizing that the goal is to reduce the system to a system of two equations with two variables. The speaker reviews the methods learned for solving systems of equations with two variables, namely elimination and graphing, and highlights the importance of eliminating a variable with a coefficient of one or negative one. The speaker then discusses the process of elimination and introduces the equations to be used in the example.

05:00
🧠 Elaborating on the Elimination Process

The speaker continues by explaining the elimination process in detail. They outline the selection of equations for the elimination of variable 'z' and demonstrate the steps of multiplying and adding equations to achieve a new set of equations with only two variables. The speaker labels these new equations as 'a' and 'b' and explains the rationale behind each step. They also discuss the flexibility in choosing different equations for elimination and the importance of understanding the process over the specific numbers used.

10:01
🔢 Solving for Variables X and Y

In this part, the speaker focuses on solving for variables X and Y using the newly formed equations 'a' and 'b'. They describe the process of eliminating 'y' by multiplying equations 'a' and 'b' with appropriate coefficients and adding them together. The speaker makes a mistake in the process, acknowledges it, and corrects it with the audience's help. They then solve for 'x' and 'y' by substituting the values back into one of the original equations, demonstrating the importance of checking work for accuracy. The speaker concludes this section by finding the value of 'z', completing the solution for the system of equations.

Mindmap
Keywords
💡System of Equations
A system of equations refers to a collection of mathematical equations that are often related and need to be solved simultaneously. In the context of the video, the focus is on a system with three variables, which complicates the process and requires specific methods to find a solution. The main goal is to reduce the complexity by eliminating one variable to make it a system of two equations with two variables.
💡Elimination Method
The elimination method is a technique used to solve systems of linear equations by adding or subtracting equations to eliminate one variable, making it easier to solve the resulting system. In the video, this method is highlighted as an effective way to reduce a system of three equations to two, by strategically choosing equations to eliminate a variable, such as z, which has a coefficient of one or negative one.
💡Substitution
Substitution is a mathematical method where one variable in a set of equations is expressed in terms of another variable, and then that expression is substituted into other equations to solve the system. Although not explicitly used in the video, it is mentioned as one of the two main strategies, along with elimination, for solving systems of equations with two variables.
💡Graphing
Graphing is a visual method of solving systems of equations by plotting the equations on a coordinate plane and finding the point(s) where the graphs intersect, which represents the solution. In the video, graphing is mentioned as a possible method for solving systems of equations, particularly with two variables, but it is not the focus of the demonstration.
💡Coefficient
A coefficient is a numerical factor that multiplies a variable in an algebraic expression or equation. In the context of the video, the speaker looks for variables with coefficients of one or negative one because they are easier to eliminate when simplifying the system of equations.
💡Variables
Variables are symbols, often letters like x, y, and z, that represent unknown quantities in an equation. In the video, the focus is on a system of equations with three variables, and the process involves reducing this to a system with two variables to simplify the solution process.
💡Solving Equations
Solving equations involves finding the values of the variables that make the equation true. In the video, the speaker is guiding the audience through the process of solving a complex system of three equations with three variables, using techniques like elimination and substitution to find the values of x, y, and z.
💡Homework Quizzes
Homework quizzes are assignments given to students to practice and reinforce the concepts learned in a lesson. In the video, the speaker acknowledges that although the homework quizzes were taken away, the provided process can still be used as a guide for understanding how to approach similar problems in the future.
💡Notes
Notes are written records of important points or information, often taken during a lecture or while learning new material. In the video, the speaker encourages the audience to take notes as a way to remember the process for solving systems of equations with three variables.
💡Educational Content
Educational content refers to material that is designed to teach or instruct, often providing information on a specific topic or subject. The video is an example of educational content, as it is focused on explaining the process of solving a complex mathematical problem involving systems of equations.
💡Mathematical Techniques
Mathematical techniques are methods or strategies used to solve mathematical problems. In the video, several techniques like elimination, substitution, and graphing are discussed as ways to solve systems of equations with multiple variables.
Highlights

Introduction to solving a system of equations with three variables.

Emphasizing the importance of reducing the system to a two-variable form.

Discussion on the elimination method and its application to systems of equations.

Explanation of the best variable to eliminate based on coefficients.

Demonstration of the elimination process with a step-by-step approach.

Selection of equations for variable elimination based on strategic choices.

Use of multiplication to modify coefficients for easier elimination.

Addition of modified equations to eliminate the chosen variable.

Result of the elimination process forming a new system of two-variable equations.

Decision to use the elimination method for the new two-variable system.

Process of eliminating y变量 from the new system of equations.

Multiplication of equations to create coefficients for elimination.

Combining the modified equations to solve for one variable.

Solution for x by dividing and simplifying the resulting equation.

Back substitution to find the values of the remaining variables y and z.

Final solution of the system of equations with x, y, and z values.

Acknowledgment of a mistake and correction during the problem-solving process.

Conclusion and summary of the problem-solving approach and results.

Transcripts

Browse More Related Video

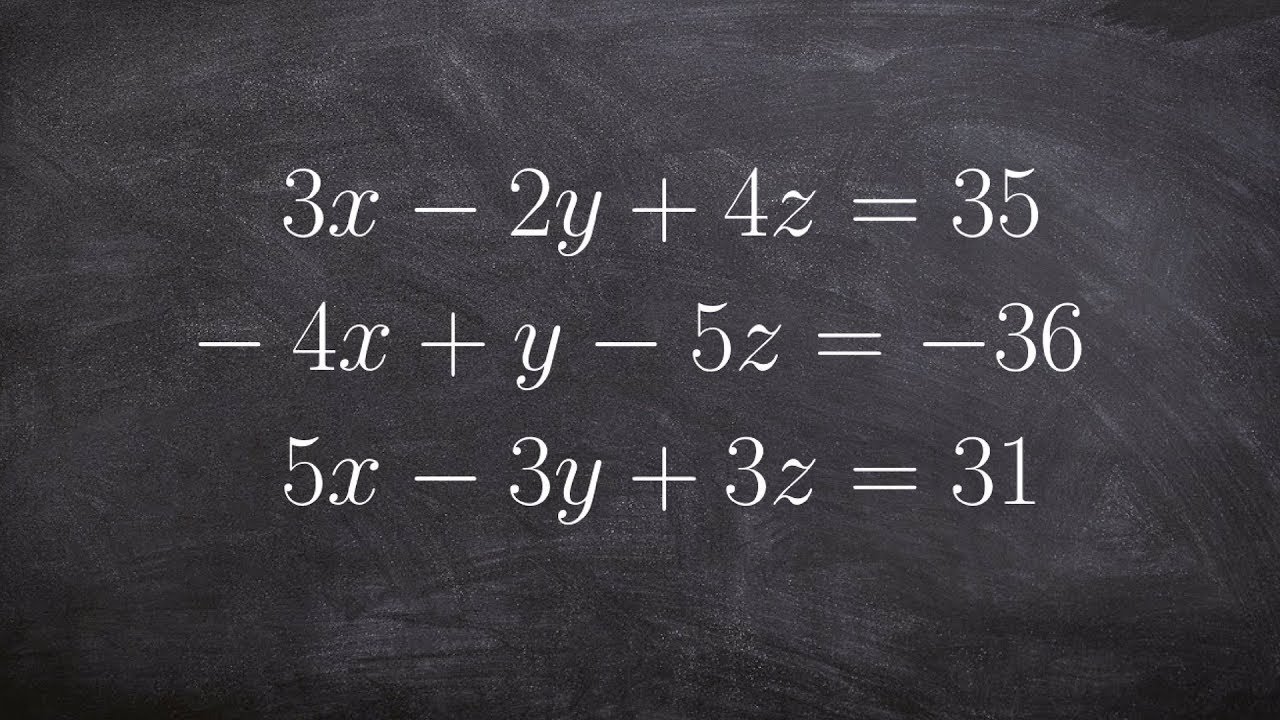
Solve a system with three variables

Gaussian Elimination With 4 Variables Using Elementary Row Operations With Matrices

PreCalculus - Matrices & Matrix Applications (7 of 33) Method of Gaussian Elimination: 3x3 Matrix*

Cramer's Rule - 3x3 Linear System

🔷11 - Gauss Jordan Elimination and Reduced Row Echelon Form

7.3.2 Gaussian Elimination

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
MathematicsAlgebraEquationsElimination MethodSubstitution MethodProblem SolvingEducational ContentInteractive LearningVariable EliminationMath Tutoring