AP Physics 1 review of Waves and Harmonic motion | Physics | Khan Academy
TLDRThe video script discusses Hooke's Law, which relates the force exerted by a spring to its extension or compression. It introduces the concept of simple harmonic motion and explains how the period of oscillation is independent of amplitude but depends on mass and spring constant for a mass-spring system, and on the length of the string for a pendulum. The script further explores waves, including transverse and longitudinal waves, and their relationship with speed, wavelength, and frequency. It also delves into the Doppler effect, wave interference, standing waves on strings and in tubes, and the concept of beat frequency. The content is rich with examples and explanations that demonstrate the principles of classical mechanics and wave physics.
Takeaways
- 📐 Hooke's Law states that the force exerted by a spring is proportional to its stretch or compression from the equilibrium length.
- 🔢 The spring constant (K) can be calculated using the formula K = mg / (L2 - L1), where L1 is the unstretched length and L2 is the stretched length with a mass (M) attached.
- 🌀 A simple harmonic oscillator's motion can be described by a sine or cosine function, with the variable being a function of time.
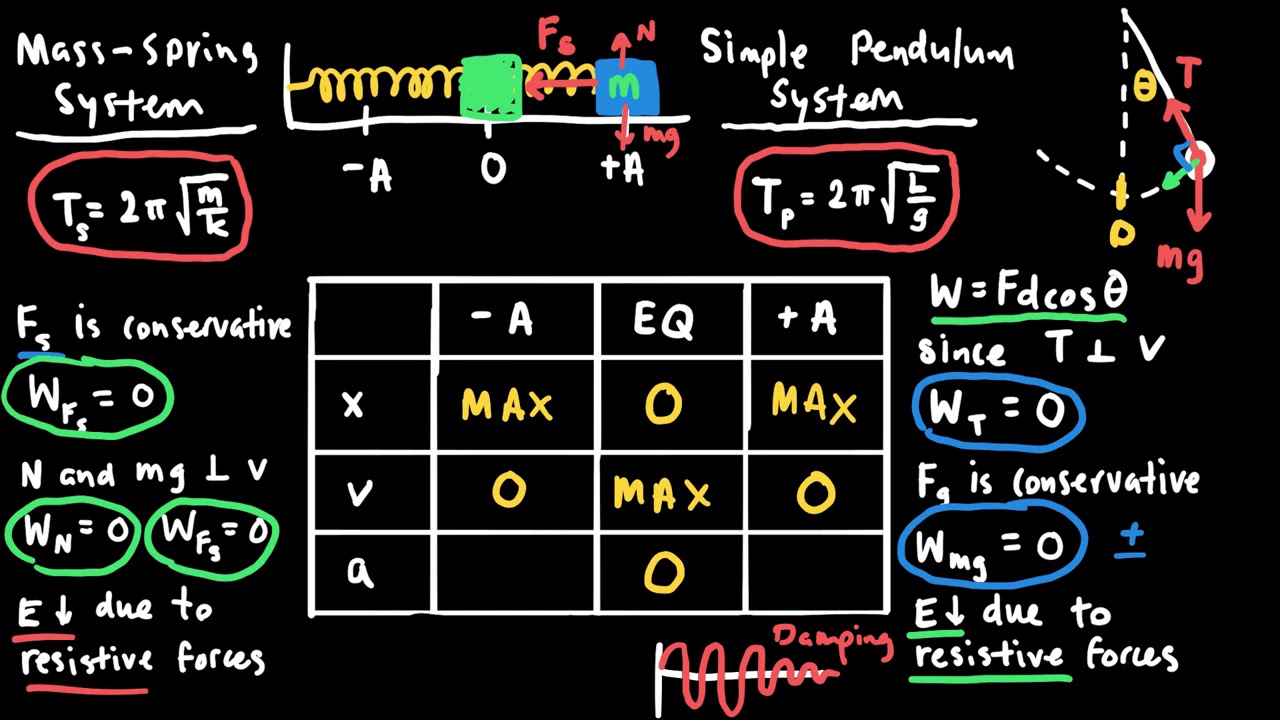
- 📶 The period of a mass-spring system is independent of amplitude and is given by T = 2π√(m/k), where m is the mass and k is the spring constant.
- ⏳ The period of a simple pendulum is also independent of mass and amplitude (for small angles), calculated as T = 2π√(L/g), where L is the string length and g is the acceleration due to gravity.
- 🌊 Waves are disturbances that transfer energy through a medium without transmitting mass, and can be classified by the medium or the type of disturbance.
- 🔽 Transverse waves have medium oscillations perpendicular to the wave velocity, like waves on a string, while longitudinal waves have oscillations parallel to the wave velocity, like sound waves in air.
- 🌐 The speed of a wave is determined by the medium's properties and is given by v = λf, where v is the wave speed, λ is the wavelength, and f is the frequency.
- 🚗 The Doppler effect describes the change in perceived frequency due to relative motion between the wave source and the observer, causing an increase or decrease in frequency based on the direction of motion.
- 🎶 Wave interference or superposition occurs when two waves overlap, combining to form a wave shape that is the sum of the individual waves, leading to constructive or destructive interference depending on their phase relationship.
- 🎸 Standing waves on strings and in tubes are determined by the medium's boundaries and length, with specific allowed wavelengths creating nodes and antinodes that do not move, resulting in a static oscillation pattern.
Q & A
What is Hooke's Law and how is it expressed mathematically?
-Hooke's Law describes the force exerted by an ideal or linear spring. It states that the force is proportional to the amount the spring has been stretched or compressed from its equilibrium position. Mathematically, it is expressed as F = k * x, where F is the spring force, k is the spring constant, and x is the displacement from the equilibrium position.
How do you calculate the spring constant in Hooke's Law using an example problem?
-To calculate the spring constant, you set up a situation where the spring is stretched by a mass and the force of gravity on the mass is balanced by the spring force. Using the formula F = k * x, and knowing that F is also equal to the weight of the mass (mg), you can solve for k by rearranging the formula to k = (mg) / (L2 - L1), where L1 is the unstretched length of the spring and L2 is the length after the mass is hung.
What is a simple harmonic oscillator and how is its motion described?
-A simple harmonic oscillator is a system whose change can be described by a sine or cosine function. The motion of a simple harmonic oscillator is given by the equation A * sin(2 * pi * (frequency * time + phase)) or A * cos(2 * pi * (frequency * time + phase)), where A is the amplitude, frequency is the oscillation rate, and phase is the initial displacement from equilibrium.
How do you determine whether to use sine or cosine in the equation for simple harmonic motion?
-The choice between sine and cosine depends on the initial conditions of the oscillator at time t=0. If the oscillator starts at the maximum displacement (amplitude) and moves towards the equilibrium position, use cosine. If it starts at the equilibrium position and moves away, use sine.
What is the formula for the period of a mass-spring system, and does it depend on the amplitude?
-The period of a mass-spring system is given by the formula T = 2 * pi * sqrt((m / k)), where m is the mass and k is the spring constant. The period does not depend on the amplitude of the oscillation.
How can you find the period of an oscillator from a graph of its motion?
-On a graph of the motion of a simple harmonic oscillator as a function of time, the period is the interval between successive peaks of the oscillation. This is the time it takes for the oscillator to complete one full cycle and return to its starting point.
What are waves and how do they transfer energy?
-Waves are disturbances that travel through a medium, transferring energy and momentum over distances without transmitting mass itself. Waves can be classified by their medium (like water, air, or string) and by the type of disturbance (transverse or longitudinal).
What is the relationship between wave speed, wavelength, and frequency?
-The speed of a wave is equal to the wavelength divided by the period, or equivalently, the wavelength times the frequency. This relationship is expressed as v = λ / T or v = λ * f, where v is the wave speed, λ is the wavelength, T is the period, and f is the frequency.
How does the Doppler effect influence the perceived frequency of a wave?
-The Doppler effect is the change in the perceived frequency of a wave when the source of the wave and the observer are moving relative to each other. If they are moving closer, the observer perceives a higher frequency due to the shorter wavelength. If they are moving apart, the observer perceives a lower frequency due to the longer wavelength.
What is wave interference and how does it affect the resulting wave?
-Wave interference, or superposition, occurs when two or more waves overlap in the same medium. The resulting wave is the sum of the individual waves' values at each point. If the waves are in phase (constructive interference), the resulting wave is larger. If they are out of phase (destructive interference), the resulting wave can be smaller or even zero.
How do standing waves on strings form and what are the conditions for their formation?
-Standing waves on strings form when waves traveling in opposite directions overlap. They require fixed or loose ends, known as nodes and antinodes, respectively. The wavelengths of the standing waves must be such that they start and end at nodes, with the fundamental frequency corresponding to half a wavelength fitting into the length of the string.
Outlines
📐 Hooke's Law and Simple Harmonic Motion
This paragraph introduces Hooke's Law, which describes the force exerted by a spring being proportional to its displacement from the equilibrium position. The spring constant (k) and the displacement (x) are defined, with an example problem given involving a hanging mass that stretches the spring. The concept of simple harmonic motion is then explored, with its sine or cosine function representation, amplitude, and the determination of using sine or cosine based on the oscillator's behavior at t=0. The period of an oscillator is derived, with examples for both a mass-spring system and a pendulum, highlighting that the period does not depend on the amplitude or mass. A graph interpretation for finding the period and wavelength of a simple harmonic oscillator's motion is also discussed.
🌊 Understanding Waves and Their Properties
This section delves into the nature of waves, defined as disturbances that transfer energy through a medium without transmitting mass. The distinction between transverse and longitudinal waves is made, with examples provided for each. The speed of wave propagation is related to the wavelength and frequency, with a clarification that changing the frequency does not alter the wave's speed, while changes in the medium's properties do. A practical example involving sound waves in a lab room is used to illustrate the principles discussed. The Doppler effect is introduced, explaining the perceived change in frequency due to relative motion between the source and the observer. Wave interference, both constructive and destructive, is also explained with examples of how waves combine when overlapping.
🌀 Wave Interference and Standing Waves
This part of the script discusses wave interference, where overlapping waves combine to form a resultant wave whose value is the sum of the individual waves. It differentiates between waves passing through each other and standing waves, which are stationary and oscillate in place. The formation of standing waves is dependent on specific wavelengths determined by the medium's boundaries. The concept of nodes and antinodes is introduced, with examples of standing waves on strings and in tubes. The behavior of standing waves with different boundary conditions, such as both ends fixed or one end loose, is explored. A method for calculating the speed of waves on a string given a standing wave is provided, as well as a discussion on standing waves in tubes and how their wavelengths are influenced by the tube's length and boundary conditions.
🔊 Beat Frequency and Wave Phenomena
The final paragraph addresses the concept of beat frequency, which occurs when two waves with different frequencies overlap and create a periodic variation in loudness. The beat period, the time taken to go from maximum constructive to destructive interference and back, is introduced, with the beat frequency defined as the number of these cycles per second. A formula to calculate the beat frequency by taking the difference between the two wave frequencies is provided. An example calculation of beat frequency for two overlapping waves with given periods is included, illustrating the concept clearly.
Mindmap
Keywords
💡Hooke's Law
💡Simple Harmonic Oscillator
💡Wavelength
💡Frequency
💡Transverse Waves
💡Longitudinal Waves
💡Doppler Effect
💡Wave Interference
💡Standing Waves
💡Beat Frequency
Highlights
Hooke's Law describes the force exerted by a spring and states that the force is proportional to the spring's displacement from its equilibrium position.
The equation for Hooke's Law is F = kx, where F is the spring force, k is the spring constant, and x is the displacement.
In a simple harmonic oscillator, the change in a variable can be described by a sine or cosine function.
The general form of the function for a simple harmonic oscillator is A sin(2πft + φ) or A cos(2πft + φ), where A is the amplitude, f is the frequency, t is the time, and φ is the phase constant.
The period of a mass-spring system is given by T = 2π√(m/k), where m is the mass and k is the spring constant.
The period of a simple pendulum is given by T = 2π√(L/g), where L is the length of the pendulum and g is the acceleration due to gravity.
Waves are disturbances that transfer energy and momentum through a medium without transmitting mass itself.
Transverse waves have medium oscillations perpendicular to the wave velocity, like waves on a string.
Longitudinal waves have medium oscillations parallel to the wave velocity, such as sound waves in air.
The speed of a wave is given by v = λf, where v is the wave speed, λ is the wavelength, and f is the frequency.
The Doppler effect describes the change in perceived frequency when the source and observer are in relative motion.
In wave interference, the total wave is the sum of individual wave values, which can result in constructive or destructive interference.
Standing waves on strings are formed by waves moving in opposite directions and have nodes and antinodes.
The length of a medium determines the allowed wavelengths for standing waves, which must start and end at nodes.
Standing waves in tubes are influenced by the tube's length and boundary conditions, such as open or closed ends.
The beat frequency is the difference in frequencies between two overlapping waves, leading to a periodic change in constructive and destructive interference.
The beat period is the time taken for the transition from loud to soft and back to loud sound, and the beat frequency is the number of these transitions per second.
Transcripts
Browse More Related Video
AP Physics 1 Simple Harmonic Motion, Mechanical Waves, and Sound Review

8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion

18. Simple Harmonic Motion (cont.) and Introduction to Waves

01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)

Anatomy of a Wave

Wave Speed on a String - Tension Force, Intensity, Power, Amplitude, Frequency - Inverse Square Law
5.0 / 5 (0 votes)
Thanks for rating: