01 - Oscillations And Simple Harmonic Motion, Part 1 (Physics Tutor)
TLDRThis comprehensive lecture introduces the concept of simple harmonic motion and its fundamental role in understanding waves. It begins with a historical overview of physics education, highlighting the progression from Newtonian motion to thermodynamics, and culminates in the study of waves. The lecture delves into oscillations, the mathematical representation of motion, and the real-life examples that illustrate these concepts. It covers the importance of understanding trigonometric functions like cosine and sine, and introduces the angular frequency and phase angle. The relationship between frequency, period, and amplitude is explored, along with the equations for position, velocity, and acceleration as functions of time. The impact of the spring constant on the oscillation frequency is discussed, and Hooke's law is introduced to describe the force exerted by a spring. The lecture concludes with a preview of the upcoming problems that will apply these concepts.
Takeaways
- 📚 The DVD set focuses on waves and their properties, with Volume 2 covering university-level physics topics related to waves.
- 🏋️♂️ Simple harmonic motion is the periodic back-and-forth motion of an object, such as a mass attached to a spring or a pendulum.
- 📐 The amplitude (A) of simple harmonic motion is the maximum displacement from the rest position, indicating how far the object moves.
- 🕰️ Frequency (F) is the number of oscillations per second and is measured in Hertz (Hz), while the period (T) is the time it takes for one complete oscillation and is inversely related to frequency (T = 1/F and F = 1/T).
- 📈 The motion of simple harmonic oscillations can be described mathematically using cosine functions, with the equation X(t) = A cos(ωt + φ), where ω is the angular frequency and φ is the phase angle.
- 📊 The velocity (V) and acceleration (A) of an oscillating object can be derived from the position function using calculus, with V(t) = -ωA sin(ωt + φ) and A(t) = -ω^2 A cos(ωt + φ).
- 🔄 The angular frequency (ω) is related to the spring constant (K) and mass (M) through Hooke's Law, with ω = √(K/M), which is crucial for determining the oscillation frequency and period.
- 📐 The phase angle (φ) in the oscillation equation determines the starting point of the graph, allowing for the adjustment of the oscillation's position on the time axis.
- 🌀 The Doppler shift and wave interference are mentioned as important wave phenomena that will be covered in the course, with applications in understanding sound waves and electromagnetic waves.
- 🔧 Hooke's law states that the force exerted by a spring is proportional to the displacement from its equilibrium position and is directed opposite to the displacement, with the formula F = -KX.
- 🌐 The course prepares students for understanding electricity and magnetism in terms of electromagnetic waves, which are all around us and interact with our daily lives.
Q & A
What is the main topic of the Ultimate Physics, Tutor Vol 2 DVD set?
-The main topic of the Ultimate Physics, Tutor Vol 2 DVD set is waves.
What is the first thing usually studied in Physics 1, either in high school or college?
-The first thing usually studied in Physics 1 is Newtonian motion, which deals with projectiles, gravity, collisions, and energy transfer.
What does the term 'simple harmonic motion' describe?
-Simple harmonic motion describes the periodic back-and-forth motion of an object about a fixed point, such as a mass attached to a spring.
How is the motion of a pendulum or a swingset an example of simple harmonic motion?
-A pendulum or a swingset exhibits simple harmonic motion because they both oscillate back and forth in a periodic manner about a fixed point, similar to the motion of a mass attached to a spring.
What is the relationship between frequency and period in simple harmonic motion?
-Frequency and period are inversely related in simple harmonic motion. The frequency is the number of oscillations per second, while the period is the time in seconds for one complete oscillation. Mathematically, the period (T) is equal to 1 divided by the frequency (F), and the frequency is equal to 1 divided by the period (F = 1/T).
What is the significance of the amplitude in simple harmonic motion?
-The amplitude in simple harmonic motion is the maximum displacement of the object from its rest position. It represents the extent of the motion and is a key characteristic of the oscillation.
What is Hooke's Law in the context of the script?
-In the context of the script, Hooke's Law states that the force exerted by a spring is equal to the negative product of the spring constant (k) and the displacement from the equilibrium position. It is represented as F = -kx.
How does the angular frequency (Omega) relate to the spring constant (k) and mass (m) in a simple harmonic motion system?
-The angular frequency (Omega) in a simple harmonic motion system is given by the square root of the spring constant (k) divided by the mass (m). Mathematically, Omega = sqrt(k/m).
What is the mathematical equation for the position of an object in simple harmonic motion as a function of time?
-The mathematical equation for the position of an object in simple harmonic motion as a function of time is given by x(t) = a * cos(Omega * t + phi), where a is the amplitude, Omega is the angular frequency, t is time, and phi is the phase angle.
What are the units for the angular frequency (Omega)?
-The units for the angular frequency (Omega) are radians per second.
How is the phase angle (phi) related to the starting conditions of the motion in simple harmonic motion?
-The phase angle (phi) in simple harmonic motion indicates where the graph of the motion starts, essentially describing the initial conditions of the motion. It shifts the graph to the right or left, depending on whether it has a positive or negative value.
Outlines
📚 Introduction to Waves and Course Overview
The speaker introduces the topic of waves and provides a brief history of the physics courses covered so far, including Newtonian motion and thermodynamics. He explains the sequence of topics and the relevance of this course on waves in the context of the entire physics curriculum. The DVD set aims to solidify the understanding of oscillations and energy transfer, preparing students for the study of electricity and magnetism in the next physics course.
🌐 Understanding Oscillations and Simple Harmonic Motion
The speaker delves into the concept of oscillations and simple harmonic motion, using everyday examples like swingsets and pendulums. He emphasizes the importance of understanding the mathematical representation of oscillations, particularly the use of cosine functions to describe the periodic motion. The speaker also introduces the idea of energy transfer in oscillations and sets the stage for discussing wave interference and the Doppler shift in future lectures.
📈 Defining Frequency, Period, and Amplitude
The speaker defines key terms related to simple harmonic motion: frequency, period, and amplitude. He explains the relationship between these terms, noting that frequency (the number of oscillations per second) and period (the time for one oscillation) are inversely related. The amplitude, or the maximum displacement from the rest position, is also described, with the speaker emphasizing its importance in understanding the extent of motion in simple harmonic systems.
🎢 Visualizing Simple Harmonic Motion with a Spring System
The speaker uses a spring system to visually demonstrate simple harmonic motion. He explains how the mass attached to the spring oscillates back and forth around its rest position, illustrating the concepts of amplitude and the speed variations at different points in the oscillation cycle. The speaker also discusses the theoretical scenario of a frictionless swing to emphasize the perpetual nature of simple harmonic motion in an ideal setting.
📊 Graphing Simple Harmonic Motion
The speaker explains how to graph simple harmonic motion, focusing on the position of the mass as a function of time. He introduces the concept of angular frequency and phase angle, which are crucial for accurately representing the oscillation on a graph. The speaker also highlights the relationship between the period of oscillation and the graphed wave, showing how the period corresponds to one complete cycle of the wave.
🔢 Mathematical Relations in Simple Harmonic Motion
The speaker establishes the mathematical relations that govern simple harmonic motion, including the formulas that connect the period, frequency, and angular frequency. He emphasizes the inverse relationship between the period and frequency, and how this translates into the angular frequency. The speaker also explains the significance of the phase angle in determining the starting point of the graphed motion.
🌟 The Equation of Simple Harmonic Motion
The speaker presents the general equation for simple harmonic motion, which includes the amplitude, angular frequency, time, and phase angle. He clarifies the roles of each component in the equation and how they contribute to the overall shape and behavior of the oscillation. The speaker also discusses the importance of understanding the angular frequency and phase angle in applying the equation to physical systems.
🚀 Hooke's Law and the Spring Constant
The speaker introduces Hooke's Law, which relates the force exerted by a spring to the displacement of the mass attached to it. He explains the concept of the spring constant (K) and how it affects the oscillation frequency and period of the system. The speaker provides formulas for calculating the angular frequency and period based on the spring constant and mass, reinforcing the connection between the physical properties of the system and its oscillatory behavior.
🎓 Conclusion and Transition to Problems
The speaker concludes the theoretical portion of the lecture by summarizing the key concepts covered, including simple harmonic motion, Hooke's Law, and the equations for angular frequency and period. He emphasizes the importance of understanding these concepts for solving the upcoming problems. The speaker then transitions to the next section, where practical problems related to the lecture material will be addressed.
Mindmap
Keywords
💡Simple Harmonic Motion
💡Amplitude
💡Frequency
💡Period
💡Angular Frequency
💡Phase Angle
💡Hooke's Law
💡Velocity
💡Acceleration
💡Wave
Highlights
Introduction to the concept of waves and their significance in physics.
Brief history of previous physics courses and their relation to the current topic.
Explanation of Newtonian motion and its relevance to physics one.
Discussion on thermodynamics and its coverage in physics DVD volume 1.
Overview of the content covered in physics volume 2 DVD.
Introduction to oscillations and their role in understanding waves.
Explanation of energy transfer in oscillations and wave formation.
Discussion on wave interference and its relation to sound waves.
Clarification on the Doppler shift and its importance in wave studies.
Preparation for physics 3 with a focus on electricity, magnetism, and electromagnetic waves.
Introduction to simple harmonic motion and Hooke's law.
Explanation of the mathematical representation of simple harmonic motion using cosine functions.
Discussion on the importance of understanding trigonometric functions for wave analysis.
Definition of frequency and its unit, Hertz, in the context of oscillations.
Explanation of the period of oscillation and its relationship with frequency.
Introduction to amplitude as a measure of maximum displacement in simple harmonic motion.
Illustration of the relationship between speed and position during simple harmonic motion.
Graphing simple harmonic motion to visualize the oscillation over time.
Derivation of the mathematical equation for simple harmonic motion.
Explanation of angular frequency and its role in converting frequency to radians for cosine functions.
Introduction to the phase angle and its impact on the starting position of the oscillation graph.
Discussion on the relationship between position, velocity, and acceleration in oscillating systems.
Transcripts
Browse More Related Video

Simple Harmonic Motion - Complete Review of the Mass-Spring System

AP Physics 1 review of Waves and Harmonic motion | Physics | Khan Academy
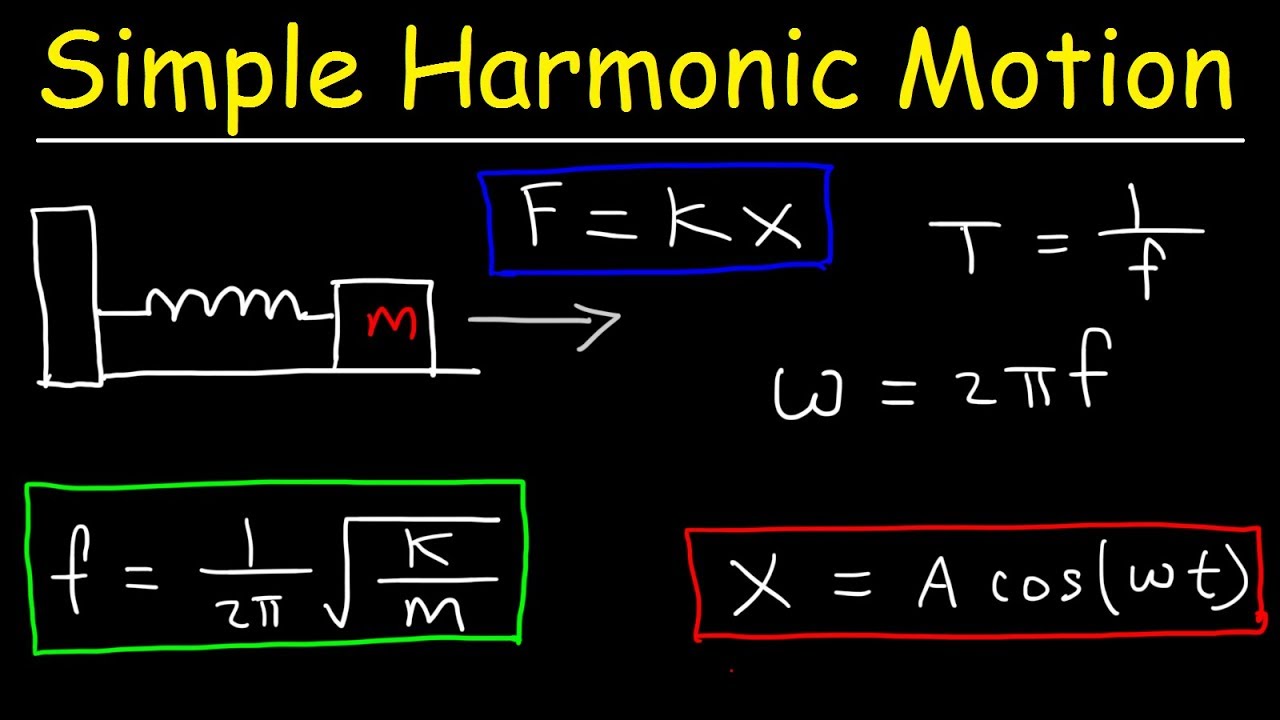
How To Solve Simple Harmonic Motion Problems In Physics
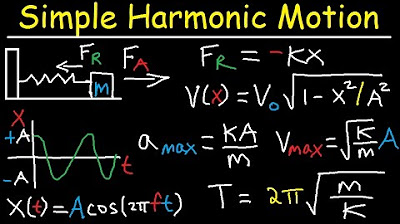
Simple Harmonic Motion, Mass Spring System - Amplitude, Frequency, Velocity - Physics Problems
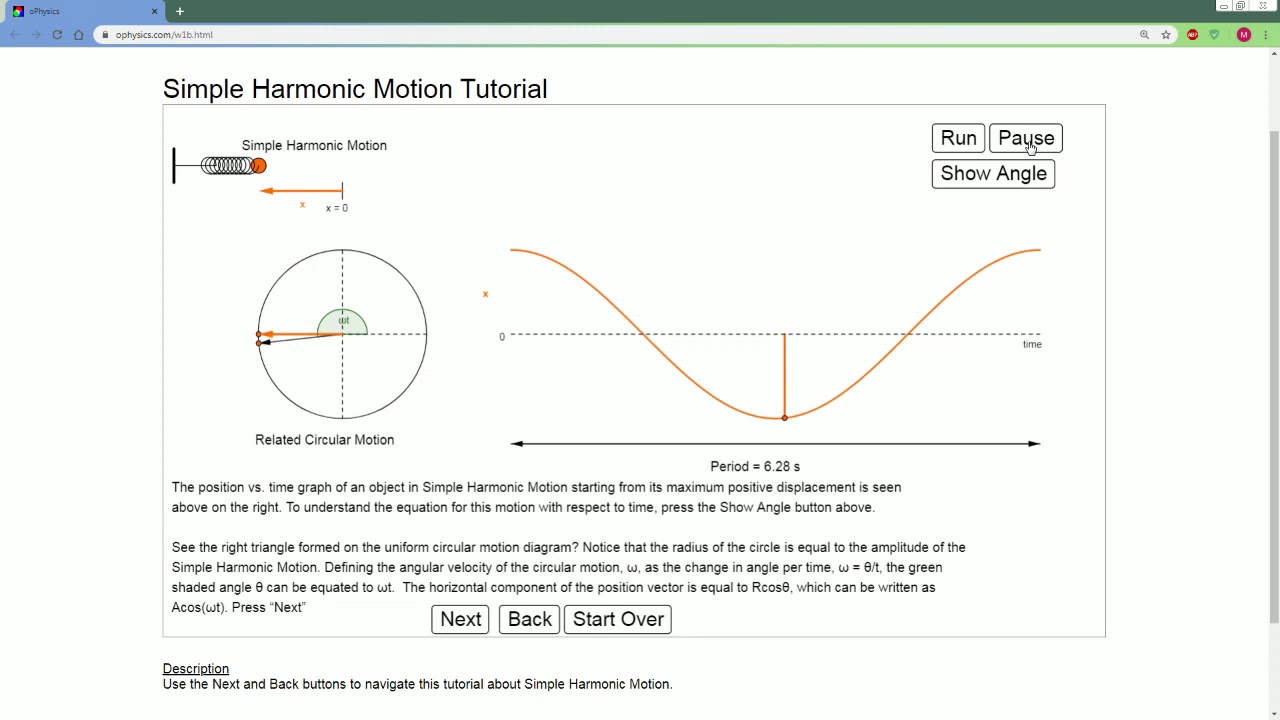
AP Physics Lecture on Simple Harmonic Motion. Watch this before 6.C
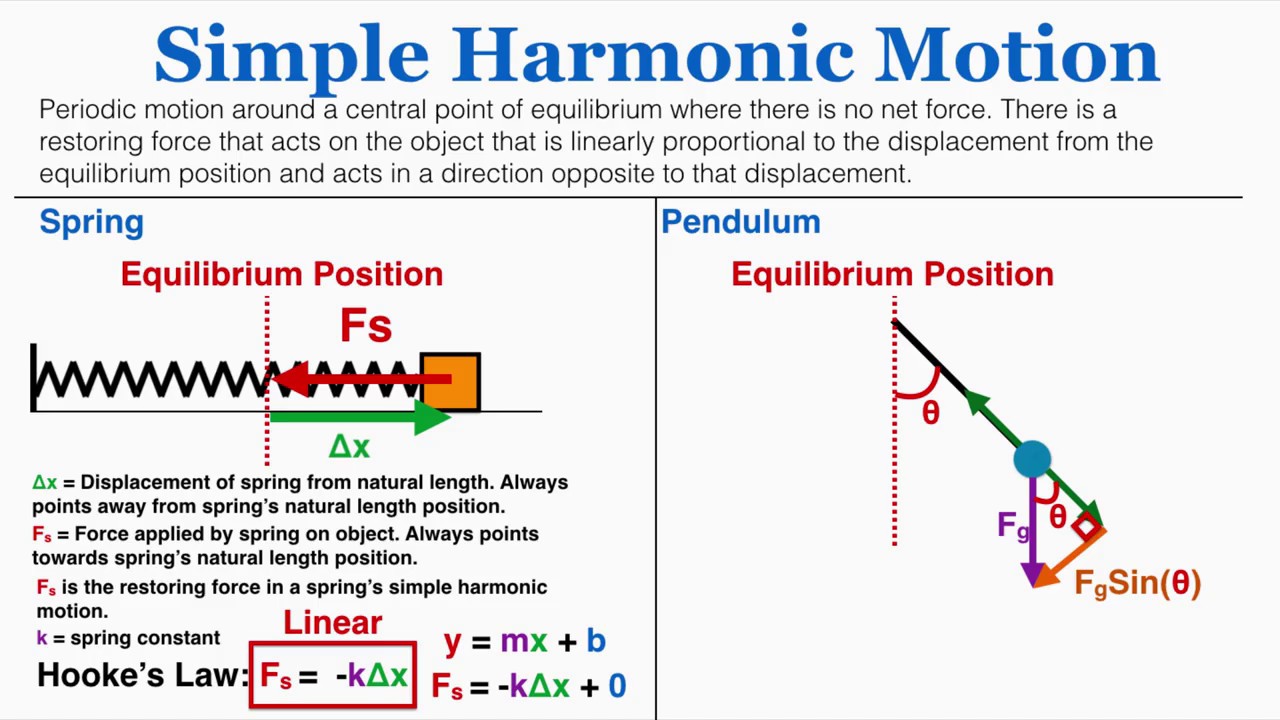
Simple Harmonic Motion - IB Physics
5.0 / 5 (0 votes)
Thanks for rating: