8.01x - Lect 10 - Hooke's Law, Springs, Pendulums, Simple Harmonic Motion
TLDRIn this engaging lecture, Professor Lewin explores the principles of simple harmonic motion, focusing on springs and pendulums. He explains Hooke's Law, detailing how the force exerted by a spring is proportional to its displacement. Lewin demonstrates how to measure the spring constant using gravity and masses, and how to calculate the period of oscillation for both springs and pendulums. He emphasizes the importance of small-angle approximations for pendulum motion and shows that the period of a pendulum is independent of its mass but depends on the length of the string and gravitational acceleration. The lecture concludes with impressive experimental validations of the theoretical predictions.
Takeaways
- 📐 Hooke's Law states that the force exerted by a spring is proportional to its displacement, with the force being negative when the displacement is positive and positive when the displacement is negative.
- 🔍 To measure the spring constant, one can hang a mass from the spring and observe the new equilibrium position, using the force of gravity on the mass.
- 📈 The spring constant (k) can be calculated from the ratio of the change in force (F) to the change in displacement (x), delta F/delta x.
- 🔄 The oscillation period of a mass attached to a spring is independent of the amplitude and is determined by the formula T = 2π√(m/k), where m is the mass and k is the spring constant.
- 🚫 Hooke's Law has limitations; if a spring is stretched beyond a certain point, it can experience permanent deformation and no longer obey the law.
- 🌐 The period of a pendulum is independent of the mass of the pendulum bob and is given by T = 2π√(l/g), where l is the length of the pendulum and g is the acceleration due to gravity.
- 📊 Small-angle approximations simplify the analysis of pendulum motion by assuming that the angle of oscillation is much less than one radian, allowing certain terms in the equations to be neglected.
- 🔄 The motion of a pendulum can be approximated as simple harmonic motion under the condition of small angles and when the string is considered massless.
- 🌌 In the absence of gravity, a pendulum would not oscillate and its period would be infinitely long, whereas a spring would still oscillate and could be used to measure mass in a weightless environment.
- 🎢 The period of a pendulum is extremely sensitive to the length of the string; changing the length by a factor of four results in the period changing by the same factor.
- 🤸♂️ Lewin's demonstration of swinging himself like a pendulum with a mass attached illustrates that the period of oscillation is indeed independent of the mass of the object.
Q & A
What is the basic principle behind the behavior of a spring described in the script?
-The basic principle is Hooke's Law, which states that the force exerted by an ideal spring to restore it to its equilibrium position is proportional to the displacement from that position, with the force being in the opposite direction of the displacement.
How is the spring constant measured in the script?
-The spring constant is measured by hanging a mass from the spring and observing the new equilibrium position. The force due to gravity on the mass is balanced by the spring force, and by plotting the force (due to different masses) against the displacement, the spring constant can be determined from the slope of the resulting straight line.
What happens when a spring is stretched beyond its elastic limit?
-When a spring is stretched beyond its elastic limit, it no longer obeys Hooke's Law, and permanent deformation occurs. The force required to stretch the spring does not increase significantly with further extension, and upon release, the spring does not return to its original length.
How does the period of oscillation for a mass attached to a spring relate to the spring constant and the mass of the object?
-The period of oscillation is independent of the amplitude and is determined by the formula T = 2π * sqrt(m/k), where T is the period, m is the mass of the object, and k is the spring constant.
What is the significance of the phase angle in the context of oscillation?
-The phase angle reflects the initial conditions of the oscillation, specifically the initial displacement and velocity. It does not affect the period of oscillation but indicates the starting point of the oscillation cycle.
How does the script demonstrate that the period of oscillation for a spring is independent of amplitude?
-The script demonstrates this by oscillating a mass on a frictionless surface and showing that the period remains constant even when the amplitude of the oscillation is changed. This is a nonintuitive result that comes from the derivation of the differential equation governing the oscillation.
What is the role of the small-angle approximation in simplifying the motion of a pendulum?
-The small-angle approximation allows us to treat the motion of a pendulum as simple harmonic motion by assuming that the angle of oscillation (theta) is very small. This approximation simplifies the differential equations of motion by making the cosine of theta approximately equal to 1 and neglecting the y-component of acceleration.
How does the period of a pendulum depend on its length and the acceleration due to gravity?
-The period of a pendulum is given by T = 2π * sqrt(l/g), where l is the length of the pendulum and g is the acceleration due to gravity. This shows that the period is directly proportional to the square root of the length and inversely proportional to the square root of the acceleration due to gravity.
What is the main difference between the period of a spring-mass system and a pendulum?
-The main difference is that the period of a spring-mass system depends on the mass of the object attached to the spring (T = 2π * sqrt(m/k)), while the period of a pendulum is independent of the mass of the object (T = 2π * sqrt(l/g)).
How does the script illustrate the concept of simple harmonic motion?
-The script illustrates simple harmonic motion through the examples of a spring-mass system and a pendulum. It shows how the periods of these systems can be calculated and how they relate to the physical properties of the systems, such as the spring constant and the length of the pendulum.
What is the significance of the experiment with the pendulum of different masses in the script?
-The experiment demonstrates that the period of a pendulum is independent of the mass of the object attached to it, which is a key characteristic of simple pendulum motion and a consequence of the small-angle approximation.
Outlines
🌟 Introduction to Springs and Simple Harmonic Oscillators
The video begins with an introduction to springs, pendulums, and simple harmonic oscillators, emphasizing their importance in the study of physics. The lecturer explains the concept of a spring's relaxed length and how extending it creates a restoring force that pushes the spring back to equilibrium. This force is proportional to the displacement and is described by Hooke's Law, where the force is equal to the spring constant (k) times the displacement (x). The spring constant can be measured using gravity and a hanging mass, allowing for the calculation of the spring's force based on the mass and displacement. The video also touches on the limitations of Hooke's Law and the potential for permanent deformation of the spring if stretched too far.
📈 Measuring the Spring Constant and Dynamic Analysis
The lecturer discusses alternative methods for measuring the spring constant, focusing on a dynamic approach that involves oscillating a mass attached to the spring on a frictionless surface. The period of oscillation is introduced as a key factor, revealing that it is dependent on the mass and the spring constant. The relationship between the period, mass, and spring constant is derived, and it is shown that the period is independent of the amplitude of oscillation. The lecturer then demonstrates this concept with a practical experiment involving a spray paint can suspended by springs and oscillating vertically, visually illustrating the sinusoidal motion of the mass as a function of time.
📊 Derivation of the Simple Harmonic Oscillator Equation
The lecturer presents a detailed derivation of the differential equation governing the motion of a simple harmonic oscillator. Starting with Newton's Second Law, the讲师 simplifies the equation by considering a massless spring and no external forces other than the spring force. The resulting second-order differential equation is then solved by assuming a sinusoidal function for the position of the mass as a function of time. The讲师 substitutes this trial solution into the differential equation and shows that the angular frequency (ω) of the oscillation is related to the spring constant (k) and the mass (m). The period of oscillation is derived and shown to be independent of the amplitude and phase angle, highlighting the fundamental characteristics of simple harmonic motion.
🌐 Application of Initial Conditions to Simple Harmonic Motion
The video explores how initial conditions, such as the initial position and velocity of the mass, determine the amplitude (A) and phase angle (φ) in the equation of motion for a simple harmonic oscillator. The lecturer provides a specific example where a mass is released from equilibrium with a given velocity, and the resulting motion is analyzed. By applying the initial conditions to the sinusoidal function, the讲师 calculates the amplitude and phase angle, demonstrating how they are influenced by the initial state of the system. The讲师 also emphasizes the importance of understanding initial conditions when solving physical problems involving oscillatory motion.
📉 Verification of the Independence of Amplitude on Period
The lecturer conducts an experiment to verify the nonintuitive concept that the period of oscillation for a simple harmonic oscillator is independent of its amplitude. Using an air track, the讲师 oscillates an object with different amplitudes and measures the periods for each case. Despite varying the amplitude, the measured periods remain consistent, confirming the theoretical prediction. The讲师 also discusses the impact of the object's mass on the period, explaining that the period is inversely proportional to the square root of the mass. This is demonstrated by combining two objects of equal mass and showing that the period for the combined system is the same as for a single object with half the mass.
🔄 Small-Angle Approximations and Pendulum Motion
The lecturer introduces the concept of small-angle approximations and their application to the motion of a pendulum. By assuming that the angle of oscillation (θ) is small, the讲师 simplifies the forces acting on the pendulum and derives the differential equations of motion. Using these equations, the讲师 shows that the motion of the pendulum can be approximated as simple harmonic oscillation, with a period that depends only on the length of the pendulum (l) and the acceleration due to gravity (g), and is independent of the mass of the pendulum bob. The lecturer emphasizes the importance of these approximations in making the mathematical analysis tractable and in understanding the fundamental behavior of the pendulum.
🎢 Comparing Spring and Pendulum Oscillations
The lecturer compares the periods of oscillation for a spring and a pendulum, highlighting the differences in how mass and length affect each system. For a spring, the period is dependent on the mass attached to it, while for a pendulum, the period is independent of the mass and only related to the length of the string and the acceleration due to gravity. The讲师 also discusses the implications of these differences, such as the ability to measure mass in a weightless environment using a spring, and the lack of pendulum motion in the absence of gravity. The video concludes with a demonstration of a large pendulum with a period of approximately 4.5 seconds, reinforcing the principles of simple harmonic motion.
🤸♂️ Physical Demonstration of Pendulum Periods
The lecturer physically demonstrates the period of a pendulum by oscillating it at different angles and measuring the time for ten oscillations. Despite varying the angle of release, the measured period remains consistent, confirming the theoretical prediction that the period is independent of the amplitude of oscillation. The lecturer also humorously involves the audience in the counting process, creating an interactive and engaging learning experience. The video concludes with a dramatic demonstration of the讲师 swinging the pendulum while sitting on it, showing that the period remains unchanged even with the讲师's added mass and motion, further illustrating the principles discussed.
Mindmap
Keywords
💡Hooke's Law
💡Spring Constant
💡Simple Harmonic Oscillator
💡Period of Oscillation
💡Amplitude
💡Angular Frequency
💡Massless Spring
💡Small-Angle Approximation
💡Phase Angle
💡Differential Equation
Highlights
Introduction to the concepts of springs, pendulums, and simple harmonic oscillators as key topics in physics.
Explanation of the relaxed length of a spring and the force that drives it back to equilibrium.
Discussion on the experimental fact that the force in many springs is proportional to displacement, known as Hooke's Law.
Method to measure the spring constant using gravity and a hanging mass.
Demonstration of how springs can be stretched beyond Hooke's Law, causing permanent deformation.
Introduction to the dynamic method of measuring the spring constant by observing oscillations.
Derivation of the differential equation for a mass attached to a spring on a frictionless surface.
Explanation of how the period of oscillation is independent of the amplitude and depends on the mass and spring constant.
Demonstration of the oscillation pattern over time using a spray paint can and springs.
Substitution of a sinusoidal function into the differential equation to find the solution for x as a function of time.
Discussion on the significance of the angular frequency, period, and phase angle in the context of oscillations.
Example calculation of the period of oscillation based on given initial conditions.
Experimental verification of the independence of the period of oscillation from the amplitude.
Discussion on the effect of mass on the period of a pendulum versus a spring.
Derivation of the pendulum's period based on small-angle approximations and comparison to the spring's period.
Demonstration of the pendulum's oscillation period and its sensitivity to the length of the string.
Conclusion on the practical applications and the remarkable agreement of theoretical predictions with experimental results.
Transcripts
Browse More Related Video

AP Physics 1 review of Waves and Harmonic motion | Physics | Khan Academy

Simple Harmonic Motion - Physics 101 / AP Physics 1 Review with Dianna Cowern
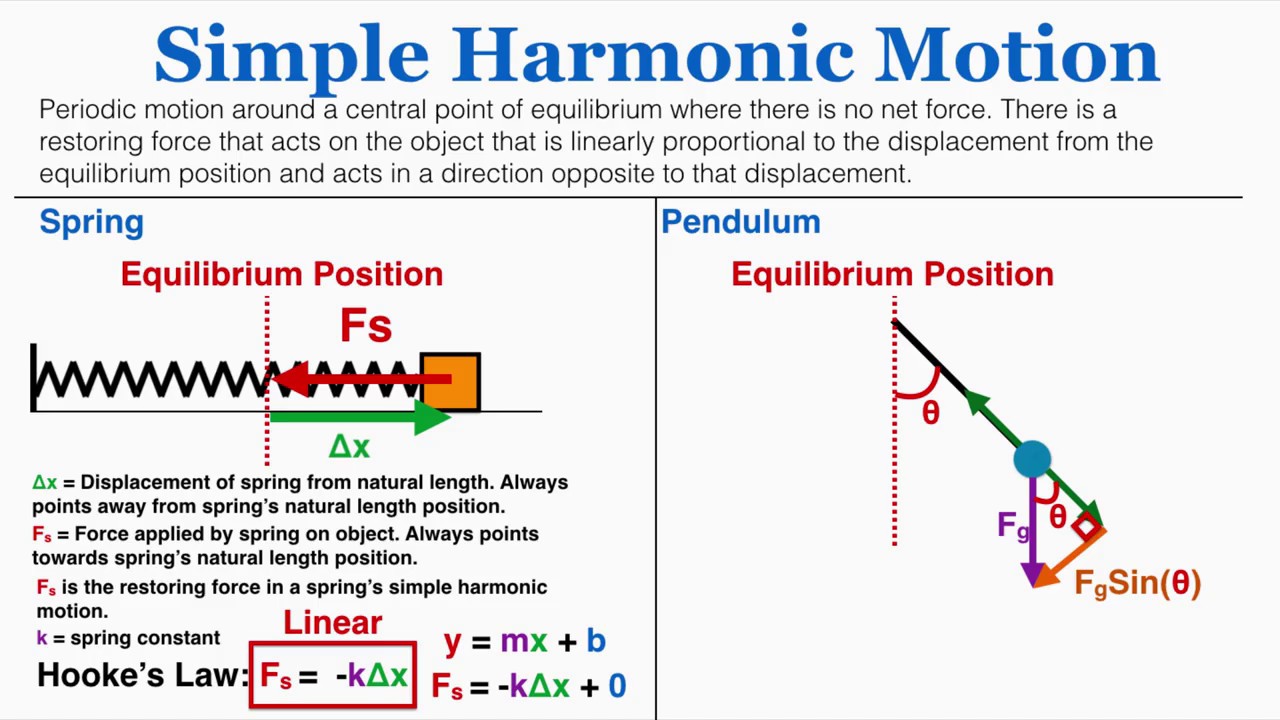
Simple Harmonic Motion - IB Physics

Pendulums | Oscillations and mechanical waves | Physics | Khan Academy
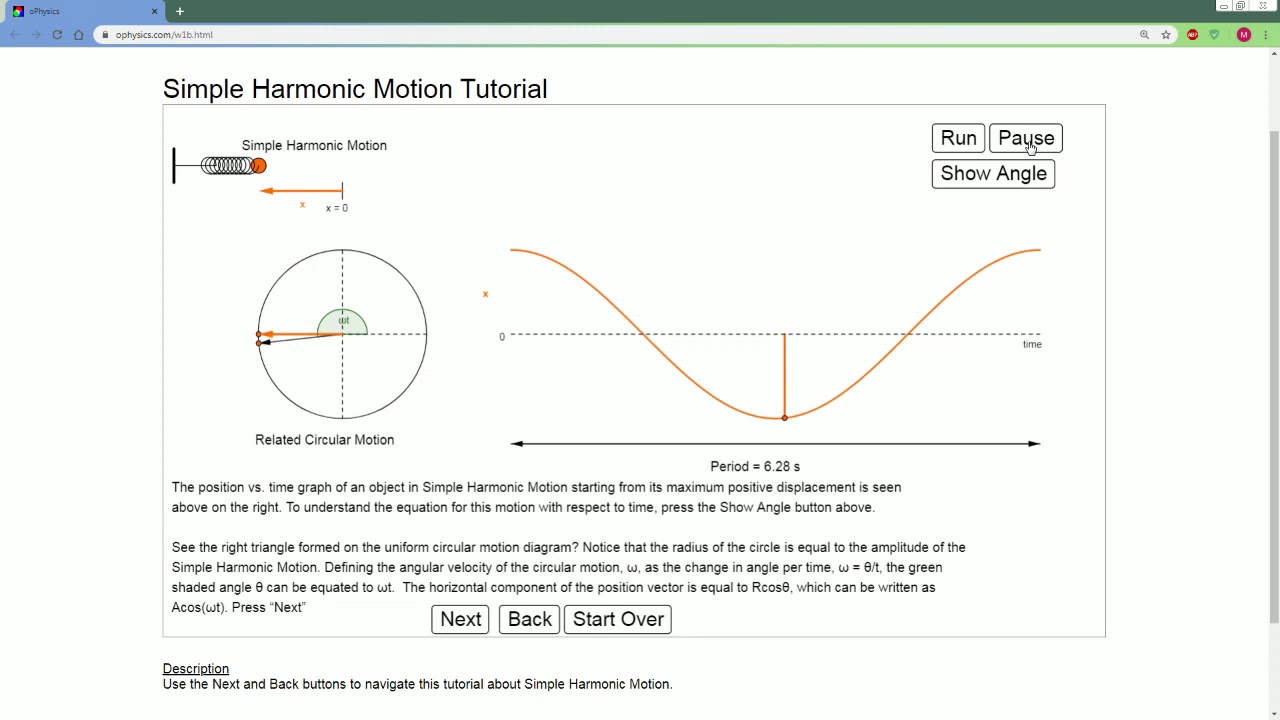
AP Physics Lecture on Simple Harmonic Motion. Watch this before 6.C

Simple harmonic motion and angular frequency [IB Physics SL/HL]
5.0 / 5 (0 votes)
Thanks for rating: