ALL OF Calculus 1 in a nutshell.
TLDRThis video script introduces the fundamental concepts of Calculus I, emphasizing the study of change and motion through functions. It explains the necessity of a one-to-one or many-to-one relationship for a set of inputs and outputs to form a function, and how the vertical line test confirms this. The script delves into limits, continuity, and the three types of discontinuities, highlighting their significance in understanding function behavior. Derivatives and their applications, such as analyzing instantaneous rates of change and optimization, are discussed, along with differentiation rules. Integration is presented as a method to calculate areas and volumes under curves, with an explanation of indefinite and definite integrals. The overview concludes by inviting viewers to explore the rich applications of calculus.
Takeaways
- 📈 The core concept of Calculus is the study of change and motion through functions.
- 📱 Functions map inputs to outputs, typically visualized as graphs in a 2D coordinate system.
- 🔍 The vertical line test is used to determine if a graph represents a function, intersecting more than once means it's not a function.
- 🎯 Limits describe how a function behaves near a point, even if it doesn't touch the point itself.
- 🔄 Continuity in functions is maintained if the function is defined at a point, the limit exists, and the function's value matches the limit's value.
- 🚧 Discontinuities occur in three forms: removable, jump, and infinite, affecting the graph of a function.
- 📌 Derivatives are used to find the rate of change or the instantaneous slope of functions at specific points.
- 🔢 Higher-order derivatives allow us to find the slope of the slope, further analyzing function behavior.
- 📚 Derivation rules like constant rule, product rule, quotient rule, etc., are essential for calculating derivatives.
- 🌍 Applications of derivatives range from determining instantaneous velocity to optimization problems.
- 📊 Integration involves finding areas under curves by summing infinitesimal slices, leading to the concept of definite integrals.
Q & A
What is the main focus of Calculus One?
-Calculus One focuses on the study of change and motion, primarily through the understanding and application of functions, limits, continuity, derivatives, and integrals.
What is a function in the context of Calculus?
-A function in Calculus is a relation that maps each input value (x-axis) to exactly one output value (y-axis), allowing for the creation of a graph. It must have either a one-to-one or many-to-one relationship and pass the vertical line test.
How can you determine if a graph represents a function?
-You can use the vertical line test to determine if a graph represents a function. If a vertical line intersects the graph at more than one point, then it is not a function.
What does the concept of limits describe in calculus?
-Limits in calculus describe how a function behaves near a certain point, even though the function may not be defined at that point. It is the value that x approaches infinitely close to, but never actually reaches.
What are the three types of discontinuities in a function?
-The three types of discontinuities are the removable discontinuity, jump discontinuity, and infinite discontinuity. Removable discontinuity occurs at a single point, jump discontinuity involves a sudden jump to another value, and infinite discontinuity is where the function diverges at an asymptote.
What is the definition of a continuous function?
-A function is considered continuous at a point if it is defined at that point, the limit exists at that point, and the value of the function at that point is equal to the limit of the function at that point.
What is the purpose of derivatives in calculus?
-Derivatives are used to find the rate of change or the instantaneous slope of a function at specific points. They are essential for analyzing changes in physical quantities such as velocity and for optimization problems.
How are derivatives represented in calculus?
-Derivatives are typically represented using the LaGrange or Leibniz notation, denoted as the derivative of a function with respect to x, often written as f'(x) or df/dx.
What are the main differentiation rules in calculus?
-The main differentiation rules include the constant rule, constant multiple rule, sum rule, difference rule, product rule, quotient rule, and chain rule. These rules help in evaluating and finding the derivatives of various functions.
How is integration used in calculus?
-Integration is used to find the areas and volumes under curves by summing up infinitely small slices under the function. It involves finding the antiderivative of a function and calculating the definite integral for a specified interval.
What are the two main types of integrals in calculus?
-The two main types of integrals are the indefinite integral, which outputs the antiderivative of a function, and the definite integral, which calculates the area under the curve of a function between two specified points (from x=a to x=b).
Outlines
📚 Introduction to Calculus and Functions
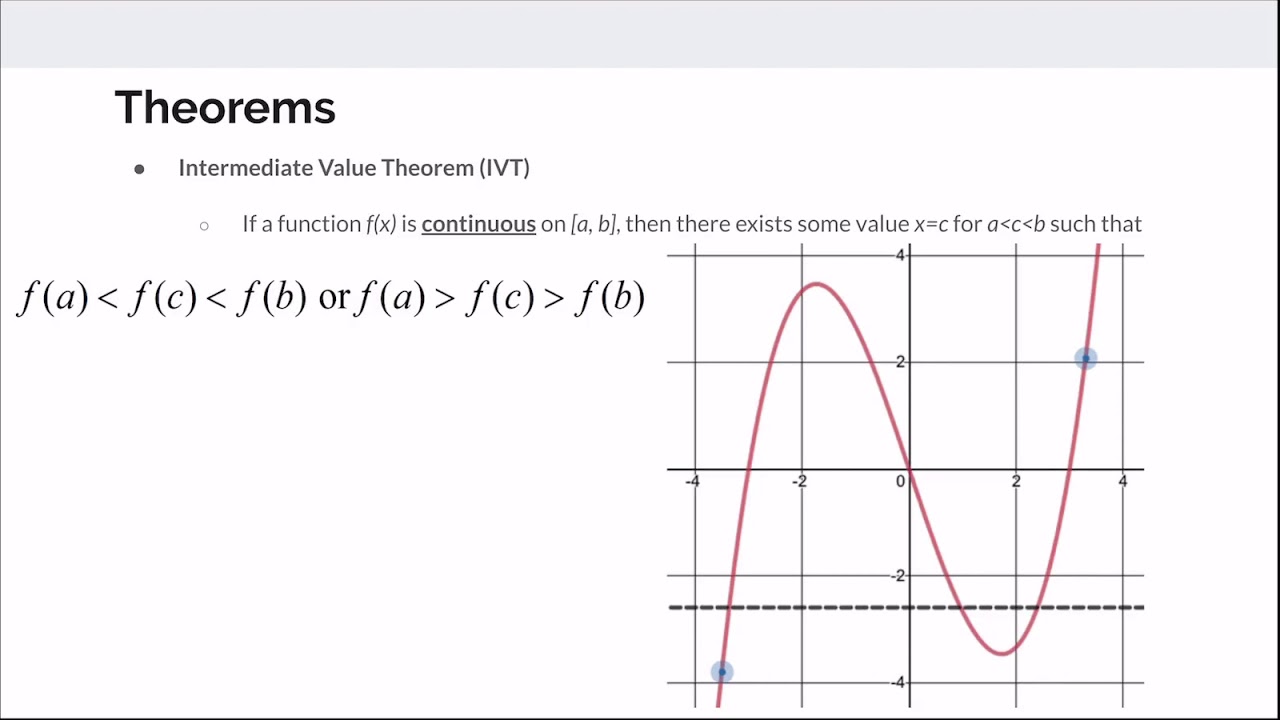
This paragraph introduces the fundamental concepts of Calculus, which is the study of change and motion. It emphasizes the importance of functions, which are relationships between sets of inputs and outputs, typically represented in 2D as graphs with inputs on the x-axis and outputs on the y-axis. The paragraph explains the necessity of functions having either a one-to-one or many-to-one relationship and introduces the vertical line test to determine if a graph represents a function. It also delves into the concept of limits, explaining how they describe a function's behavior near a point without actually touching it. The general expression for limits is provided, highlighting the idea of a value that x approaches but never reaches. The paragraph concludes by discussing the three types of discontinuities: the removable discontinuity, jump discontinuity, and infinite discontinuity, and the conditions for a function to be considered continuous.
📈 Derivatives, Differentiation Rules, and Applications
This paragraph focuses on derivatives, which are instrumental in analyzing the rate of change of functions, providing insights into the instantaneous slope at specific points. It introduces the concept of higher-order derivatives, which represent the slope of the slope. The paragraph then outlines the differentiation rules, including the constant rule, constant multiple rule, sum rule, difference rule, product rule, quotient rule, and chain rule. It also highlights the practical applications of derivatives, such as determining instantaneous velocity and optimization problems. The discussion then shifts to integration, which is used to calculate the areas and volumes under curves. The paragraph describes the process of integration, starting from slicing the area under the curve into rectangles to eventually summing an infinite number of infinitesimally small slices to obtain the exact area. It concludes by distinguishing between the two types of integrals: the indefinite integral, which outputs the antiderivative of a function, and the definite integral, which calculates the area under the curve between two points.
🎓 Summary of Calculus One
The final paragraph serves as a concise summary of the key points covered in Calculus One. It reiterates the foundational concepts of functions, limits, continuity, and the importance of derivatives and integrals in understanding the behavior of functions and their applications. The paragraph encapsulates the essence of calculus, emphasizing the journey from basic functions to more complex concepts such as optimization and area calculation under curves. It concludes by acknowledging that while some details were left out, the provided information offers a solid foundation and a starting point for delving deeper into the beautiful world of calculus.
Mindmap
Keywords
💡Calculus
💡Functions
💡Limits
💡Continuity
💡Derivatives
💡Differentiation Rules
💡Integration
💡Indefinite Integral
💡Definite Integral
💡Vertical Line Test
💡Discontinuities
Highlights
Calculus is fundamentally the study of change and motion.
Functions are the foundation of calculus, relating a set of inputs to a set of outputs.
In a 2D space, functions take an input on the x-axis and output a value on the y-axis, creating a graph.
A function must have a one-to-one or many-to-one relationship to be valid, which can be tested using the vertical line test.
Limits describe how a function behaves near a point, even though it does not include the point itself.
The general expression for limits is \( \lim_{x \to a} f(x) = l \), which is read as 'the limit of f of x as x approaches a is the value l'.
Discontinuities occur when limits do not exist or diverge, and can be of three types: removable, jump, or infinite.
A function is considered continuous at a point if it is defined there, the limit exists, and the function's value equals the limit's value.
Derivatives are used in calculus to analyze the rate of change of functions, providing the instantaneous slope at certain points.
Derivatives are denoted using the LaGrange and Leibniz notation, and higher-order derivatives can be taken to find the slope of the slope.
Differentiation rules, such as constant rule, sum rule, product rule, quotient rule, and chain rule, are used to evaluate and calculate derivatives.
Derivatives have practical applications in determining instantaneous velocity and optimization problems to find maximum or minimum values.
Integration involves finding areas and volumes under curves by summing up infinitely small slices.
There are two types of integrals: indefinite integrals, which output the antiderivative of a function, and definite integrals, which calculate the area under the curve.
Integration starts with a rough approximation by slicing the area under the curve into rectangles and refines as the number of slices increases.
The journey into calculus begins with understanding these fundamental concepts that open up a world of mathematical beauty and practical applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: