1.3 - Average Rates of Change
TLDRThe video script delves into the foundational concept of 'rates of change' in calculus, focusing on how function values or outputs alter with varying input values. It distinguishes between two types of change: the average rate of change, calculated over an interval, and the instantaneous rate of change, examined at a precise point. The script introduces the average rate of change formula, illustrating its geometric interpretation as the slope of a secant line between two points on a function's curve. The concept of the difference quotient is also explored, serving as a preliminary to more advanced calculus topics. Through examples using functions like f(x) = x^2, the script demonstrates how to calculate the average rate of change and the difference quotient, emphasizing their significance in understanding the behavior of functions. The summary underscores the script's aim to prepare viewers for further study in calculus, particularly the integration of limits with the difference quotient.
Takeaways
- 📈 The concept of rates of change is central to calculus, focusing on how function values (outputs) change with input values (x-values).
- 🔢 There are two types of rates of change: average rate of change, which measures the change over an interval, and instantaneous rate of change, which focuses on the change at a single point.
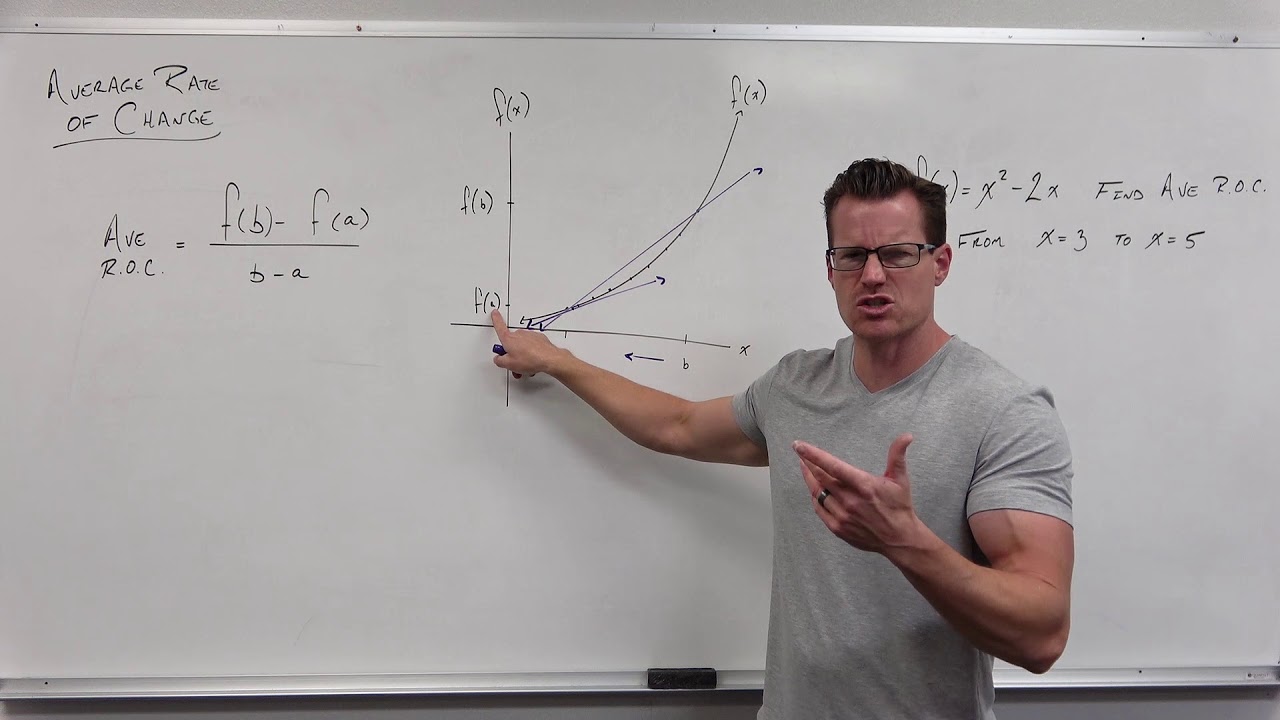
- 📖 The average rate of change is calculated by finding the difference in y-values (f(x2) - f(x1)) and dividing by the difference in x-values (x2 - x1), akin to the slope formula for a line.
- 📐 Geometrically, the average rate of change corresponds to the slope of the secant line that passes through two points on a curve.
- 📉 As the interval between x-values decreases, the average rate of change approaches the instantaneous rate of change, which is the focus of further calculus discussions.
- 📌 Function notation can be used to represent the average rate of change more generally as (f(x2) - f(x1)) / (x2 - x1).
- ➗ The difference quotient is a formula used to calculate the average rate of change and is defined as (f(x + h) - f(x)) / h, where h represents a small change in the input value.
- 🔑 The difference quotient is logically equivalent to the average rate of change and is used to find the simplified form of the rate of change for various functions.
- 📐 For a linear function, such as f(x) = x^2, the difference quotient simplifies to a form that can be used to find the rate of change for any x and h values.
- 🤔 The process of simplifying the difference quotient involves algebraic manipulation and can vary depending on the type of function (polynomial, rational, radical).
- ➡️ The difference quotient is a precursor to the concept of derivatives in calculus, which deal with instantaneous rates of change and are found using limits.
Q & A
What is the main focus of calculus?
-The main focus of calculus is the study of continuous change, particularly how function values (outputs) change as input values change.
What are the two types of rates of change discussed in the video?
-The two types of rates of change discussed are the average rate of change and the instantaneous rate of change.
How is the average rate of change of a function defined?
-The average rate of change of a function is defined as the change in y values (output) divided by the associated change in x values (input) over a specific interval.
What is the geometric representation of the average rate of change?
-The geometric representation of the average rate of change is the slope of the secant line that passes through two points on the curve of the function.
What is the difference quotient?
-The difference quotient is an expression representing the average rate of change of a function and is defined as (f(x + h) - f(x)) / h, where f(x) is the function and h is the change in the input value.
Why is the difference quotient important in calculus?
-The difference quotient is important because it is used to extend the concept of average rate of change to the idea of instantaneous rate of change, which is a fundamental concept in calculus.
How does the average rate of change relate to the slope of a line?
-The average rate of change is closely related to the slope of a line, especially when dealing with linear functions. It represents the change in y values per unit change in x values, similar to how slope is calculated.
What happens to the average rate of change as the x values get closer to each other?
-As the x values get closer to each other, the average rate of change becomes smaller. This is because the function values at those points are closer together, resulting in a smaller rate of change over a smaller distance.
What is the purpose of calculating the difference quotient for different values of h?
-Calculating the difference quotient for different values of h helps to understand how the rate of change of the function behaves as we get closer to a specific point on the function, which is essential for studying instantaneous rates of change.
How does the simplified form of the difference quotient help in evaluating it for specific values?
-The simplified form of the difference quotient allows for a quicker and more efficient way to evaluate the rate of change for any given x and h values without having to start the calculations from scratch each time.
What is the relationship between the difference quotient and the concept of limits in calculus?
-The difference quotient is used in conjunction with limits to define the instantaneous rate of change at a single point. As h approaches zero, the difference quotient is used to find the derivative of the function at that point, which is a fundamental operation in calculus.
Outlines
📈 Introduction to Rates of Change in Calculus
The video begins by introducing the concept of rates of change, which is central to the study of calculus. It differentiates between two types of change: average rate of change, which measures the change over an interval, and instantaneous rate of change, which focuses on the change at a specific point. The average rate of change is defined as the change in y-values (outputs) divided by the change in x-values (inputs) between two points on a function. This is analogous to the slope of a line, but it applies to any function, not just linear ones. The geometric representation of this is the slope of the secant line passing through two points on the function's curve.
🔍 Calculating Average Rate of Change with Function Notation
The video provides a method for calculating the average rate of change using function notation. It demonstrates how to find the average rate of change for a given function, f(x) = x^2 + 1, over different intervals. The process involves finding the function values at the endpoints of the interval and using these to calculate the average rate of change. The video emphasizes that this calculation is akin to finding the slope of a secant line between two points on the curve of the function.
📐 Understanding the Difference Quotient and Its Graphical Interpretation
The video explains the difference quotient, another expression for the average rate of change, which is logically equivalent to the previous formulas but uses a different labeling scheme. The difference quotient is defined as (f(x + h) - f(x)) / h, where h represents a small change in the x-value. The video illustrates that this formula represents the slope of a secant line between a point on the function and a nearby point. Simplifying the difference quotient for the function f(x) = x^2 yields a general formula that can be used for any x and h values.
🔢 Evaluating the Difference Quotient with Specific Values
The video demonstrates how to evaluate the difference quotient for specific values of x and h, using the function f(x) = x^2. It shows that as the distance h decreases, the rate of change approaches the instantaneous rate of change at x. This is similar to the concept of limits in calculus, where values are considered to be increasingly close to a point of interest. The video concludes by noting that using a simplified form of the difference quotient is more efficient than recalculating it from scratch each time.
🧮 Simplifying the Difference Quotient for Various Functions
The video discusses the process of simplifying the difference quotient for different types of functions, such as polynomial, rational, and radical functions. It emphasizes that the more complex the function, the more involved the simplification process becomes. For a rational function g(x) = 1/x, the video shows how to find a common denominator and simplify the difference quotient. For a radical function h(x) = √x, the conjugate multiplication method is introduced to simplify the expression. The goal in each case is to eliminate the h in the denominator and arrive at a simplified formula for the difference quotient.
📚 Summary of Average Rate of Change and Difference Quotient
The video concludes with a summary of the concepts covered. It reiterates that the average rate of change over an interval is modeled geometrically by the slope of a secant line on the function's graph. The difference quotient is a formula that can be simplified for any function, which is essential for extending the concept to calculus. The video hints at the future discussion on limits and how they will be combined with the difference quotient to define a fundamental concept in calculus.
Mindmap
Keywords
💡Average Rate of Change
💡Instantaneous Rate of Change
💡Function Notation
💡Secant Line
💡Tangent Line
💡Difference Quotient
💡Limits
💡Continuous Change
💡Slope
💡Function Values
💡Graphical Representation
Highlights
Calculus is the study of continuous change, focusing on how function values change with input values.
Two types of change are discussed: average rate of change and instantaneous rate of change.
The average rate of change is calculated over an interval and is akin to the slope of a line between two points on a function.
Function notation is introduced to represent the change in function values (f(x2) - f(x1)) over the change in input values (x2 - x1).
The geometric interpretation of average rate of change is the slope of the secant line through two points on a curve.
Instantaneous rate of change focuses on the change at a single point, which will be explored in more detail later.
The concept of the difference quotient is introduced as a method to calculate the average rate of change.
The difference quotient is logically equivalent to the average rate of change formula but uses a different labeling scheme.
The difference quotient is defined as (f(x + h) - f(x))/h and is used to find the slope of the secant line between points.
As the distance between x values decreases, the rate of change also becomes smaller, indicating a more localized change.
Examples are provided to show how to calculate the average rate of change for different intervals using a given function.
The importance of function notation (f(x)) is emphasized for its utility in representing changes in function values over intervals.
The video demonstrates the process of simplifying the difference quotient for specific functions, such as f(x) = x^2.
The simplified form of the difference quotient can be used as a formula for any combination of x and h values.
The concept of limits is alluded to as a future topic that will formalize the idea of shrinking the distance h to approach instantaneous change.
Different strategies are used for simplifying the difference quotient based on the type of function, such as polynomial, rational, or radical functions.
The video concludes with a summary of the average rate of change and the difference quotient, setting the stage for further exploration into calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: