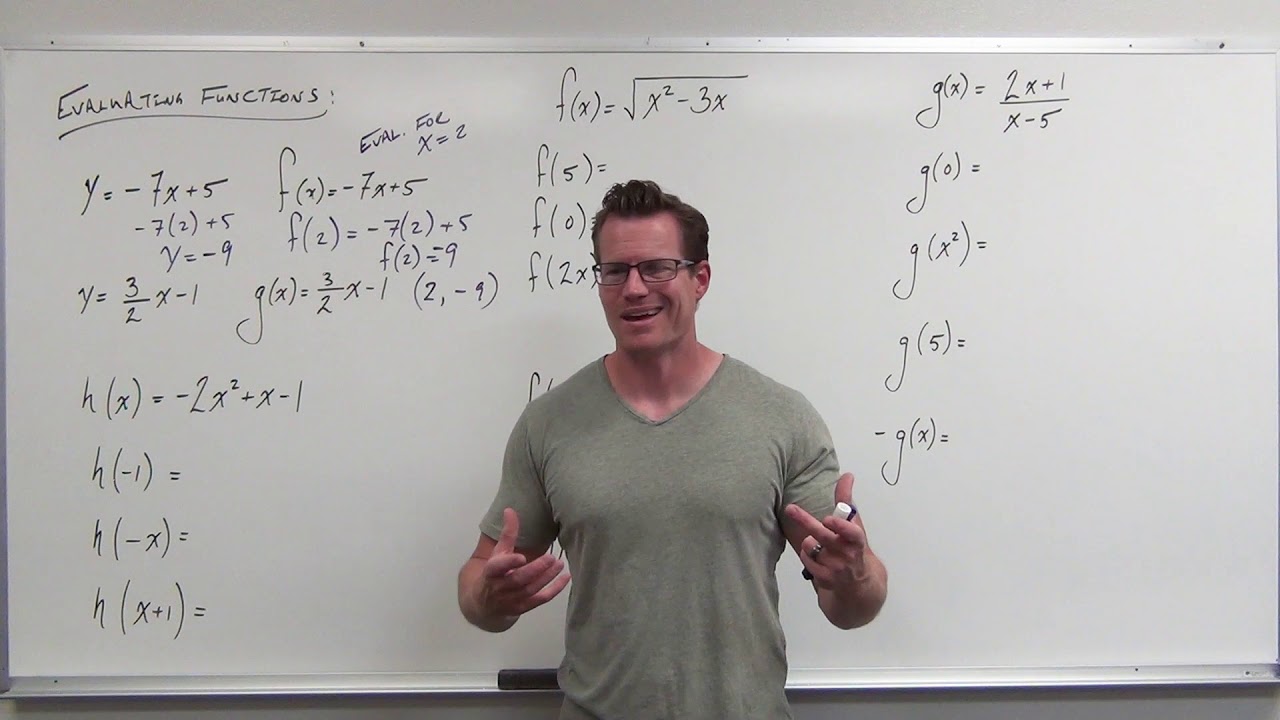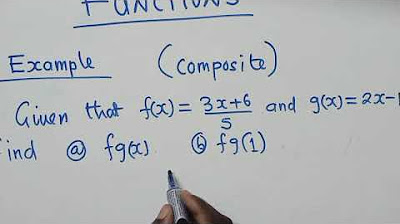Calculus made EASY! 5 Concepts you MUST KNOW before taking calculus!
TLDRIn this informative video, Dr. Ji introduces five fundamental math concepts crucial for understanding calculus. Starting with function notation, the video explains the role of input (independent variable) and output (dependent variable), and how to represent functions algebraically and graphically. The importance of understanding linear functions, including slope calculation and point-slope form, is emphasized. The video also delves into exponent rules, particularly rational and negative exponents, and their applications. Domain and range concepts, including interval and set notation, are clarified. Lastly, the concept of composite functions is introduced, highlighting how outputs of one function can be inputs for another. The video assures viewers that mastering these basics will greatly ease the transition into calculus.
Takeaways
- 📚 Function Notation: Understanding function notation is crucial for calculus, where f(x) represents the output for a given input x.
- 🔢 Linear Functions: Familiarity with slope (m) and the point-slope form is essential, even for non-linear functions, to find the secant line between two points.
- 💡 Exponents: Mastery of rational exponents, negative exponents, and extracting greatest common factors with exponents is vital for simplifying expressions in calculus.
- 📈 Domain and Range: Knowledge of interval and set notation is important for curve sketching and analyzing the behavior of functions across different intervals.
- 🔄 Composite Functions: Recognizing and working with composite functions (F(g(x))) is a key concept, as well as being able to decompose them into simpler functions.
- 🔍 Evaluating Functions: Learning to find inputs and outputs both algebraically and graphically is necessary for understanding function behavior and solving problems.
- 📊 Graph Interpretation: Interpreting graphs to find points, evaluate functions, and determine the existence of outputs is a practical skill for calculus.
- 🌐 Coordinate Representation: Representing points on a function using coordinates (x, f(x)) helps in understanding the relationship between inputs and outputs.
- 📌 Secant Lines: Understanding that the slope of a line connecting two points on a curve represents the secant line, not the function's slope, is important for calculus.
- 📚 Precalculus Foundation: While calculus builds upon precalculus knowledge, focusing on these five key concepts provides a solid foundation for further study.
- 🎓 Encouragement for Learning: The video emphasizes that with a good grasp of these basic concepts, learners can approach calculus with confidence and success.
Q & A
What are the five important math concepts covered in the video?
-The five important math concepts covered in the video are function notation, linear functions, exponents, domain and range, and composite functions.
What is function notation and why is it important in calculus?
-Function notation is a way to represent a function with a variable, typically using f(x) where x is the input. It's important in calculus because it simplifies the representation of functions and their outputs, making it easier to understand and manipulate functions in various calculations.
How do you represent the output of a function when the input is a specific number?
-To represent the output of a function when the input is a specific number, you replace the variable in the function's formula with that number. For example, if the function is f(x) = 2x + 1 and you want to find the output when x = 2, you would calculate f(2) = 2*2 + 1 = 5.
What is the slope of a linear function and how is it calculated?
-The slope of a linear function is a measure of how steep the line is and is represented by the letter m. It is calculated using the rise over run formula, which is (y2 - y1) / (x2 - x1), where (x1, y1) and (x2, y2) are two points on the line.
What is the purpose of the point-slope form in linear functions?
-The point-slope form is used to describe the equation of a line when you know the slope of the line and a point on the line. It is given by the formula (y - y1) = m(x - x1), where m is the slope and (x1, y1) is the known point.
What are rational exponents and how are they used in calculus?
-Rational exponents are expressions that involve both a radical (root) and a fractional exponent. In calculus, rational exponents are used to convert between radical forms and fractional exponents, which is important for simplifying expressions and performing various calculations.
What is the negative exponent rule and how does it apply in calculus?
-The negative exponent rule states that a number raised to a negative exponent is equal to the reciprocal of that number raised to the positive exponent. In calculus, this rule is often used to eliminate fractions by rewriting expressions with negative exponents as positive exponents, simplifying further calculations.
How do you express the domain and range of a function in interval notation?
-In interval notation, the domain and range of a function are expressed using parentheses and brackets to indicate inclusivity or exclusivity of the endpoints. For example, an interval from -4 to 4 inclusive would be written as [-4, 4]. An open circle indicates exclusivity (not including the endpoint), while a closed circle indicates inclusivity (including the endpoint).
What is a composite function and how is it represented?
-A composite function is a function that takes the output of one function and uses it as the input for another function. It is represented as F(g(x)), which means the function F is applied to the result of the function g(x). This concept is crucial in calculus for understanding how functions interact with each other.
How do you identify and work with composite functions in calculus?
-In calculus, you identify composite functions by recognizing that one function's output is being used as the input for another function. To work with them, you often need to simplify the composite function by substituting the inner function's output into the outer function and then simplifying the resulting expression.
What is the significance of understanding the concepts of domain, range, and composite functions before starting calculus?
-Understanding the concepts of domain, range, and composite functions before starting calculus is significant because these concepts form the foundation for more advanced topics in calculus. They help in analyzing and graphing functions, performing algebraic manipulations, and comprehending the behavior of functions, which are essential skills for success in calculus.
Outlines
📚 Introduction to Calculus: Essential Math Concepts
Dr. Ji introduces the video by emphasizing the importance of understanding five key math concepts before delving into calculus. These concepts are not exhaustive but are crucial for easing the transition into calculus. The first concept discussed is function notation, which is deemed the most important. The video explains the basics of functions, including inputs (independent variables), outputs (dependent variables), and how to represent functions using function notation. The concept is illustrated using linear and piecewise functions, and the video demonstrates how to find outputs for given inputs and vice versa. The application of function notation in representing coordinates of points on a function is also covered.
📈 Understanding Graphs and Linear Functions
This paragraph focuses on the graphical representation of functions and linear equations. It explains how to interpret graphs and find inputs or outputs by visually scanning the graph. The video introduces the concept of slope in linear functions, explaining its calculation and how it relates to secant lines on a graph. The paragraph also discusses the point-slope form of linear equations and touches on converting these into slope-intercept form. The importance of understanding these concepts for calculus is highlighted, particularly in the context of curve sketching and analyzing the behavior of functions.
🔢 Exponents and Their Applications in Calculus
The third paragraph delves into the world of exponents, highlighting three key rules or applications crucial for calculus. These include rational exponents, negative exponents, and extracting the greatest common factor with exponents. The video provides examples of how to convert between radical and rational exponents, the significance of negative exponents in simplifying fractions, and the process of factoring out the greatest common factor from expressions with exponents. The explanation is geared towards preparing viewers for the complexities of calculus, where these concepts are frequently applied.
📊 Domain and Range: Interval and Set Notations
This section introduces the concepts of domain and range, explaining the difference between interval and set notation. The video clarifies the use of brackets and parentheses in interval notation to denote inclusivity or exclusivity of values. It also covers the representation of infinity in interval notation. Set notation is briefly discussed, with examples of how to express domain and range using greater than, less than, and equality symbols. The paragraph emphasizes the practical application of interval notation in calculus, particularly for curve sketching and analyzing the intervals where a graph exhibits certain behaviors.
🔄 Composite Functions: Structure and Simplification
The final paragraph of the video script discusses composite functions, which involve substituting the output of one function into another function. The process of creating composite functions is explained, along with the notation used to represent them. The video provides examples of how to break down complex composite functions into simpler functions. It also touches on the reverse process of decomposing composite functions into their constituent parts, which is an essential skill in calculus. The video concludes by encouraging viewers to master these concepts for a smoother transition into calculus, and invites engagement through likes, subscriptions, and comments.
Mindmap
Keywords
💡Function Notation
💡Independent Variable
💡Dependent Variable
💡Piecewise Function
💡Slope
💡Exponents
💡Domain and Range
💡Composite Functions
💡Rational Exponents
💡Negative Exponents
💡Greatest Common Factor (GCF)
Highlights
Dr. Ji introduces five key math concepts essential for understanding calculus.
Function notation is emphasized as the most important concept, simplifying the understanding of inputs and outputs.
The dependent variable (y) and independent variable (x) are explained within the context of a function.
Piecewise functions are introduced as a type of function that doesn't follow a single equation pattern.
The concept of replacing variables in functions to find outputs is demonstrated.
The algebraic process of solving for an input given an output is outlined.
Function notation is used to represent coordinates of points on a function graph.
The importance of understanding linear functions and their slopes in calculus is discussed.
The calculation of slope using two points on a graph is explained, including the concept of secant lines.
Exponents and their applications, including rational and negative exponents, are highlighted as crucial for calculus.
The process of factoring out the greatest common factors with exponents is detailed.
Domain and range are introduced with interval and set notations, important for curve sketching in calculus.
Composite functions are defined and their role in inserting the output of one function into another is explained.
The ability to break down composite functions into their original functions is emphasized for calculus.
The video concludes with an encouragement for viewers to apply these concepts to make calculus easier.
The presenter invites viewers to like the video and subscribe to the channel for more educational content.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: