Calculus in 20 Minutes with Professor Edward Burger
TLDRThe video script offers a rapid-fire introduction to calculus, covering its fundamental concepts in under 20 minutes. It explains the two core issues of calculus: finding the instantaneous rate of change and calculating areas under curves. The script introduces the derivative as the solution to the first problem and demonstrates how it relates to the slope of a tangent line. It also touches on the applications of calculus, including linear approximation, optimization problems, and graphing functions. The video concludes with a brief mention of antiderivatives and the fundamental theorem of calculus, which allows for the computation of areas under curves by integrating from one point to another.
Takeaways
- 📌 The two fundamental questions of calculus are finding instantaneous rate of change and calculating areas under curves.
- 🔄 Instantaneous rate of change is the slope of the tangent line at a particular point on a curve, representing how quickly something is changing at that instant.
- 📈 To find the slope of a tangent line, we use the concept of limits to approach the 'zero over zero' problem and define the derivative.
- 📚 The derivative is the limit as Δx approaches zero, represented as the limit of (f(x+Δx) - f(x)) / Δx.
- 🔢 The derivative can be used for various applications such as finding maxima or minima, linear approximation, and related rates.
- 🌐 The process of finding the area under a curve is based on the fundamental theorem of calculus, which involves integrating the function from point A to point B.
- 🧩 Integration is the reverse process of differentiation, and it helps in finding antiderivatives, which are useful in solving various problems like motion and distance.
- 🔄 The antiderivative, or indefinite integral, of a function can be found using various rules such as power rules, substitution, and the chain rule.
- 📊 Calculus allows us to analyze complex functions by finding critical points, determining increasing/decreasing intervals, and identifying points of inflection using first and second derivatives.
- 🛠️ The concept of related rates can be used to find unknown rates of change when given one rate and a relationship described by an equation, using implicit differentiation.
- 🎓 Understanding calculus requires a solid foundation in the concepts of limits, derivatives, and integrals, and the ability to apply them to a wide range of problems.
Q & A
What are the two main questions addressed in calculus?
-The two main questions addressed in calculus are: 1) How do you find the instantaneous rate of change, and 2) How do you find the areas under curves.
What is the relationship between instantaneous rate of change and the slope of a line?
-The instantaneous rate of change is equal to the slope of the tangent line at a particular point on a curve. As the points on a secant line get closer together, the slope of the resulting line approaches the slope of the tangent line.
How is the concept of a limit used in calculus?
-The concept of a limit is used in calculus to deal with indeterminate forms, such as 0/0, that arise when trying to find instantaneous rates of change. By taking the limit as the change in time (ΔT) or change in distance (ΔX) approaches zero, we can find the unique value the function approaches, which allows us to determine the instantaneous rate of change.
What is the definition of the derivative?
-The derivative is defined as the limit as ΔX goes to zero of the expression (f(X + ΔX) - f(X)) / ΔX. It represents the instantaneous rate of change of a function at a specific point and gives the slope of the tangent line at that point.
What are the main rules for taking derivatives of more complicated functions?
-The main rules for taking derivatives of more complicated functions include the product rule, quotient rule, and chain rule. The product rule involves multiplying the derivative of the first term by the second term plus the second term's derivative by the first term. The quotient rule states that the derivative of a quotient is the bottom times the derivative of the top minus the top times the bottom's derivative, all divided by the bottom squared. The chain rule is used when dealing with composite functions and involves taking the derivative of the outer function and multiplying it by the derivative of the inner function.
How can you find the derivative of a function using implicit differentiation?
-Implicit differentiation is used when the function is given as a relation, such as x^2 + y^2 = 1. To find the derivative with respect to X (dy/dx), you differentiate both sides of the equation with respect to X, treat y as a function of X, and solve for the derivative.
What is linear approximation and how is it used?
-Linear approximation is a method used to estimate the value of a function at a specific point when the exact value is not known. It involves finding the equation of the tangent line at a known point and then plugging in the unknown point to approximate the value. This technique is useful for making calculations and is the basis for how computers perform calculus.
How do you find maxima and minima using calculus?
-To find maxima and minima using calculus, you take the derivative of the function and set it equal to zero or find where the derivative does not exist (but the function does). These points are candidates for local maxima or minima. The first derivative test can then be used to determine whether these points are indeed maxima or minima by checking the sign of the derivative around these critical points.
What is the fundamental theorem of calculus and how does it relate to finding areas under curves?
-The fundamental theorem of calculus connects differentiation and integration. It states that if you want to find the area under a curve from point A to point B, you can do so by integrating the function f(X) from A to B. The area is given by the antiderivative F(X) evaluated at B minus F(X) evaluated at A, i.e., ∫ from A to B f(X) dX = F(B) - F(A).
How can you use calculus to analyze motion?
-By taking derivatives of different orders, you can analyze various aspects of motion. The first derivative represents velocity, the second derivative represents acceleration, and so on. By integrating these derivatives, you can find the position and displacement over time. This allows you to model and analyze the motion of objects in both horizontal and vertical planes.
What are asymptotes and how do they relate to functions?
-Asymptotes are lines that a function approaches but never reaches. A vertical asymptote occurs when the denominator of a function equals zero (after simplification), while a horizontal asymptote occurs when the limit of the function as X approaches infinity or negative infinity equals a certain value. Asymptotes can be used to understand the behavior of functions at certain values of X and provide insights into the graph of the function.
Outlines
📚 Introduction to Calculus and Instantaneous Rate of Change
This paragraph introduces the fundamental concepts of calculus, focusing on two main questions: finding the instantaneous rate of change and determining areas under curves. It explains that these seemingly separate questions are, in fact, closely related. The discussion begins with the definition of rate as change in distance over change in time, leading to the concept of a slope on a graph. The average rate of change between two points is shown to be the slope of the line connecting these points. The instantaneous rate is then approached by shrinking this line (secant line) to a point, resulting in a tangent line whose slope represents the instantaneous rate of change. The challenge of dealing with a zero over zero indeterminate form is introduced, setting the stage for the use of limits to find the derivative, which is the central concept for addressing both main questions.
🔢 Derivatives, Rules, and Applications
This paragraph delves deeper into the concept of derivatives, explaining how to calculate them for various types of functions. It introduces the product rule, quotient rule, and chain rule for more complex functions, providing a brief overview of how each rule is applied. The paragraph also touches on implicit differentiation for relations that aren't explicitly functions. Further applications of derivatives are discussed, such as finding instantaneous velocity and acceleration from velocity, as well as using derivatives for linear approximation and determining maxima and minima. The importance of understanding the problem, listing known facts, and finding relationships to solve problems is emphasized, a method applicable to all of life's challenges.
📈 Maxima, Minima, and Related Rates
This section continues the exploration of calculus by discussing the use of derivatives to find maxima and minima, and to solve related rate problems. It explains how setting the derivative equal to zero or finding where it is undefined can help identify potential maximum and minimum values. The concept of linear approximation is also revisited, with an emphasis on using tangent lines for approximation. The related rates topic is introduced, showing how knowledge of one rate of change can be used to find another related rate, using the Pythagorean theorem as an example. The paragraph concludes with a brief mention of graphing functions using derivatives to determine critical points, concavity, and inflection points, as well as the concept of asymptotes for exotic functions.
🧠 Antiderivatives and the Fundamental Theorem of Calculus
The final paragraph shifts focus to antiderivatives and the process of integration. It provides a formula for finding antiderivatives of basic functions and introduces the concept of substitution for more complex integrals. The integration of velocity to find position and the application of calculus to the study of motion are discussed. The paragraph culminates in explaining the fundamental theorem of calculus, which allows for the calculation of areas under curves by integrating from one point to another. The process is illustrated with an example, showing how to find the area under a curve from point A to point B by using the antiderivative. The paragraph concludes by highlighting the ability to calculate areas under more complex curves and reiterates the comprehensive nature of calculus, encouraging further exploration and application of the concepts learned.
Mindmap
Keywords
💡Calculus
💡Instantaneous Rate of Change
💡Derivative
💡Tangent Line
💡Secant Line
💡Limit
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Implicit Differentiation
💡Linear Approximation
Highlights
The introduction of the two fundamental questions of calculus: finding instantaneous rate of change and calculating areas under curves.
Understanding rate as change in distance over change in time, and its relation to the slope of a line.
The concept of a secant line and its average rate of change in relation to the slope of the line connecting two points on a graph.
The distinction between average rate and instantaneous rate of change, and the convergence towards a tangent line for the latter.
The introduction of the derivative as the limit as Delta X approaches zero, representing the instantaneous rate of change.
The explanation of the zero over zero problem in calculus and the method of approaching the zero point to resolve it.
The application of calculus in determining the limit of a function and its significance.
The rules for taking derivatives of complicated functions, such as the product rule, quotient rule, and chain rule.
The concept of implicit differentiation and its use in differentiating relations rather than explicit functions.
The use of derivatives in finding instantaneous velocity and further in determining acceleration through second derivatives.
The method of linear approximation to estimate the value of a function at a certain point using the tangent line approximation.
The use of calculus in identifying maxima and minima by finding where the derivative equals zero or does not exist.
The fundamental method of solving problems by understanding the question, listing known facts, and finding relationships.
The application of related rates in calculating changing rates when one rate is known, using connections like the Pythagorean theorem.
The process of graphing functions accurately by identifying critical points, using the first and second derivative tests, and understanding the function's concavity.
The concept of antiderivatives and the fundamental theorem of calculus, which relates the process of integration to finding areas under curves.
The method of substitution as a technique for integrating complicated functions by transforming them into simpler forms.
The comprehensive summary of calculus concepts, including the application of integration in various scenarios such as calculating areas and analyzing motion.
Transcripts
Browse More Related Video

Why Are Slope and Area Opposite: The Fundamental Theorem of Calculus

Business Calculus - Math 1329 - Section 5.3 - The Definite Integral and Fundamental Thm of Calculus
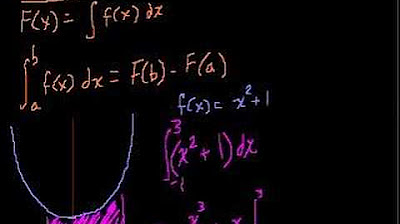
Definite Integrals (part 4)
What Integral Calculus Is — Topic 85 of Machine Learning Foundations

ALL OF Calculus 1 in a nutshell.

Mastering Calculus: An Introduction to Integrals
5.0 / 5 (0 votes)
Thanks for rating: