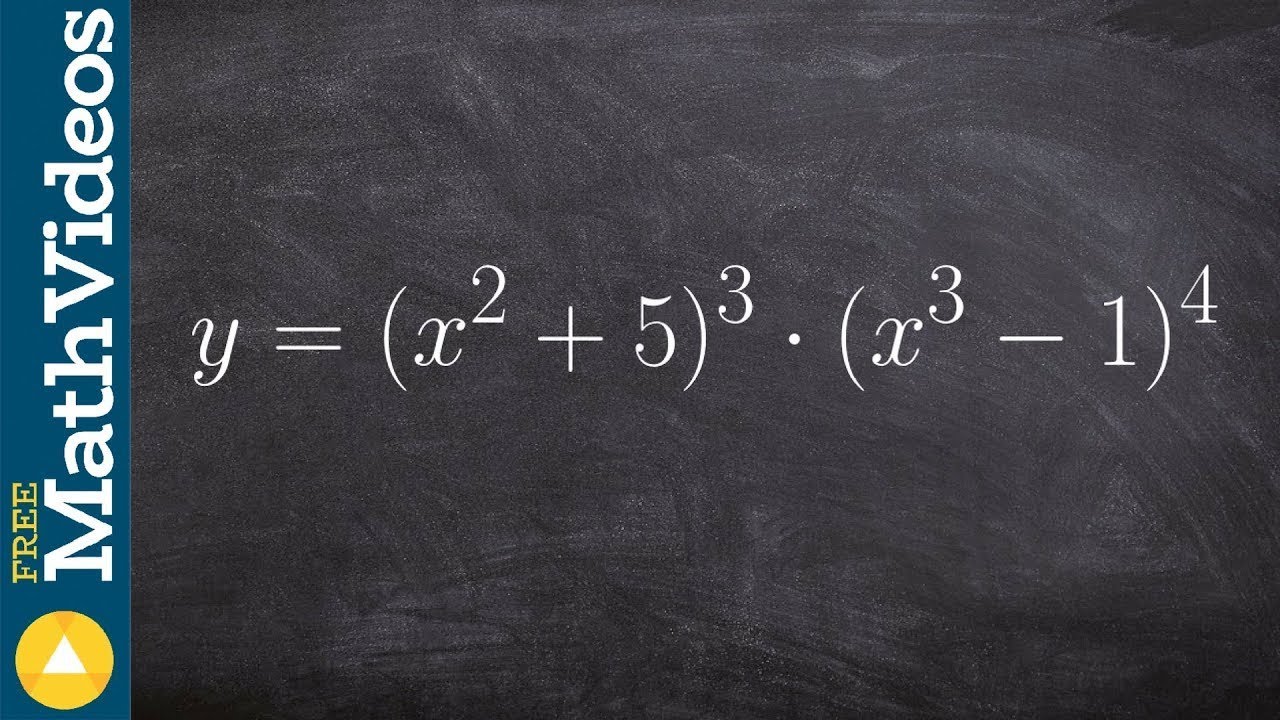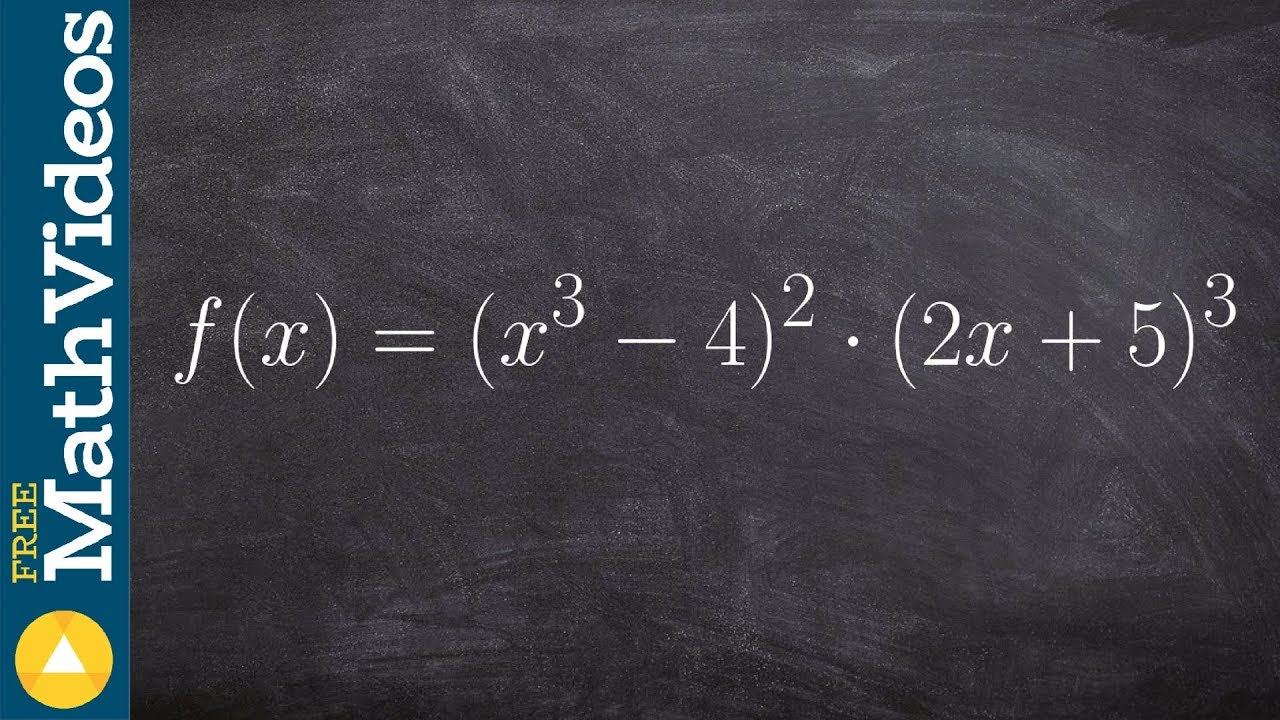Simplifying Derivatives
TLDRThis video lesson focuses on simplifying derivatives using the product and chain rules. The instructor demonstrates the process with two example problems, showing how to find the derivatives of complex functions. The first example involves differentiating a function of the form x^3(2x - 5)^4, using the product rule and chain rule to simplify the expression and factor out the greatest common factor. The second example tackles the derivative of x^2 times the square root of (4 - 9x), again applying the product rule and chain rule, and explaining how to rationalize the denominator if required. The lesson is a comprehensive guide to mastering these calculus concepts.
Takeaways
- 📚 The lesson focuses on simplifying derivatives using the product and chain rules.
- 🧮 For the function x^3 * (2x - 5)^4, apply the product rule to find the derivative.
- 📈 Calculate the derivative of x^3 as 3x^2, and use the chain rule for differentiating (2x - 5)^4.
- 🔢 Factor out the greatest common factor (GCF) to simplify the expression after applying the rules.
- 🌟 For the second example, x^2 * √(4 - 9x), again use the product rule to differentiate.
- 🛠 Differentiate x^2 to get 2x and apply the chain rule to differentiate √(4 - 9x).
- 📊 Rewrite the square root as a rational exponent to simplify the expression further.
- 🤝 Combine like terms and find common denominators for the terms involving x.
- 🌐 Factor out the lowest exponent for terms with negative exponents in the denominator.
- 📝 The final answer for the second derivative can be left in radical form or rationalized if required.
- 🎓 Understanding the chain rule and power rule is crucial for differentiating composite functions.
- 🔍 Practice identifying and factoring out GCFs to simplify derivatives and improve problem-solving efficiency.
Q & A
What is the main focus of the lesson?
-The main focus of the lesson is simplifying derivatives, specifically using the product rule and chain rule.
What is the product rule used for in differentiation?
-The product rule is used for differentiating the product of two functions. It states that the derivative of a function f times g is the derivative of f (f') times g plus f times the derivative of g (g').
What is the formula for the product rule?
-The formula for the product rule is (f * g)' = f' * g + f * g'.
What is the chain rule used for in differentiation?
-The chain rule is used for differentiating composite functions. It involves differentiating the outer function and then multiplying by the derivative of the inner function.
How is the derivative of x cubed calculated?
-The derivative of x cubed is calculated using the power rule, which states that the derivative of x^n is n*x^(n-1). Thus, the derivative of x cubed (x^3) is 3x^2.
What is the process for finding the derivative of 2x - 5 raised to the fourth power?
-To find the derivative of 2x - 5 raised to the fourth power, you use the chain rule. First, differentiate the outer function (which is the fourth power) to get 4*(2x - 5)^3. Then, differentiate the inner function (2x - 5) to get 2, and multiply the two results.
How can the expression 3x^2 * (2x - 5)^4 + 8x * (2x - 5)^3 be simplified?
-The expression can be simplified by factoring out the greatest common factor (GCF). In this case, x^2 and (2x - 5)^3 are factored out, leaving 3 * (2x - 5) and 8x after distributing and combining like terms.
What is the derivative of x squared times the square root of 4 - 9x?
-The derivative is found by using the product rule. First, differentiate x squared to get 2x and keep the square root part the same. Then, differentiate the square root of 4 - 9x using the chain rule, which involves differentiating 4 - 9x and multiplying by the derivative of the square root function.
How do you rationalize the denominator when asked to do so?
-To rationalize the denominator, you multiply both the numerator and the denominator by the conjugate of the denominator. In the context of the script, this would involve multiplying by the square root of 4 - 9x to eliminate the negative exponent in the denominator.
What is the final simplified form of the derivative for the function x squared times the square root of 4 - 9x?
-The final simplified form is x * (8 - 45/2 * x) / sqrt(4 - 9x), or if rationalizing the denominator is not required, x * (8 - 45x/2) / (4 - 9x)^(1/2).
What is the importance of factoring out the GCF in simplifying derivatives?
-Factoring out the GCF simplifies the expression and makes it easier to work with. It also helps in reducing the complexity of the calculations and can reveal patterns or symmetries in the expression that can be useful for further manipulations.
How does the power rule apply to the term (2x - 5)^4 in the first example?
-The power rule applies by differentiating the term inside the parentheses first, which is 2x - 5, and then raising the result to the fourth power. The derivative of 2x - 5 is 2, and applying the power rule, we get 4 * (2x - 5)^3.
Outlines
📚 Simplifying Derivatives using Product and Chain Rules
This paragraph introduces the concept of simplifying derivatives, focusing on the application of the product rule for a function involving x cubed times (2x - 5) to the fourth power. The explanation begins with identifying the function parts, f and g, and proceeds to calculate their derivatives using the product and chain rules. The process involves finding the derivative of x cubed, applying the chain rule to (2x - 5) to the fourth power, and then combining these results. The simplification of the expression is achieved by factoring out the greatest common factor (GCF), x squared, and 2x - 5 to the third power, resulting in a final simplified derivative.
📈 Applying the Chain Rule to a Composite Function
This section delves into the application of the chain rule for differentiating a composite function. The example given is the derivative of x squared times the square root of (4 - 9x). The explanation starts by using the product rule to differentiate the first part of the function, x squared, resulting in 2x. The second part, the square root of (4 - 9x), is then addressed using the chain rule. The process involves rewriting the expression in radical form and factoring out the GCF, which in this case is x raised to the power of negative one-half. The summary highlights the importance of factoring out the lower exponent when dealing with negative exponents and demonstrates how to simplify the expression by distributing and combining like terms, ultimately resulting in a final answer that can be left in radical form or further rationalized as required.
📝 Rationalizing the Denominator for a Square Root Expression
The final paragraph discusses the optional step of rationalizing the denominator of a square root expression. It builds upon the previous example, where the derivative was left in a form involving a square root in the denominator. The explanation outlines the process of multiplying both the numerator and the denominator by the square root of (4 - 9x) to achieve a rationalized form. The summary emphasizes that while the radical form is acceptable, the rationalized form can be provided if necessary, offering flexibility in presenting the final answer.
Mindmap
Keywords
💡Derivative
💡Product Rule
💡Chain Rule
💡Power Rule
💡Greatest Common Factor (GCF)
💡Rational Exponent
💡Simplifying Expressions
💡Composite Function
💡Differentiation
💡Like Terms
💡Combining Terms
Highlights
The lesson focuses on simplifying derivatives using an example problem involving the derivative of a function composed of x cubed times 2x minus 5 raised to the fourth power.
The product rule is introduced and explained, which is used to find the derivative of a product of two functions.
The derivative of x cubed is calculated as 3x squared, showcasing the use of basic power rule.
The chain rule is applied to find the derivative of (2x - 5) raised to the fourth power, highlighting its importance in dealing with composite functions.
The process of factoring out the greatest common factor (GCF) is discussed as a method to simplify the expression.
An example of the derivative of x squared times the square root of 4 - 9x is provided to illustrate the application of the product rule.
The power rule is used again to differentiate the outer function of x squared, resulting in 2x.
The chain rule is applied a second time to differentiate the inner function (4 - 9x) raised to the one half.
The concept of rational exponents is introduced and used to simplify the expression further.
The method of factoring out terms with negative exponents is explained, leading to a more simplified form of the expression.
The process of distributing and combining like terms is detailed to arrive at the final simplified form of the derivative.
The final answer is expressed in a form involving a radical, showcasing the application of algebraic simplification techniques.
An alternative form of the final answer is presented, where the denominator is rationalized if required.
The lesson emphasizes the importance of understanding and applying the product rule and chain rule for solving complex derivative problems.
The process of simplifying derivatives is demonstrated step by step, providing a clear and comprehensive guide for learners.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: