Higher Order Derivatives!
TLDRThe video script focuses on the concept of higher order derivatives, starting with an example of the function x cubed and its successive derivatives. It explains the notation for higher order derivatives, using tick marks or parentheses to denote the order. The script then delves into examples using the chain rule, product rule, and quotient rule for finding derivatives of functions like f(x) = 3(2 - x)^3 and g(x) = (1 - 4x) / (x - 3), and emphasizes the importance of simplifying the first derivative before proceeding to the second and beyond. The video aims to help viewers understand the process of finding higher order derivatives and the algebraic manipulation required to simplify expressions, making the task more manageable.
Takeaways
- 📚 Section 9.8 is focused on higher order derivatives, which are the derivatives of derivatives.
- 🔍 The motivation for studying higher order derivatives is that functions like x^3 can be differentiated multiple times.
- 📈 Derivatives can be denoted with tick marks (e.g., y'' for second derivative) or using terms like 'f double prime' for the second derivative of f(x).
- 🌟 You can find higher order derivatives by adding more tick marks or using parentheses to denote the order (e.g., y^(4) for the fourth derivative).
- ∞ The derivative of zero is always zero, and you can derive a function infinitely many times.
- 🔑 The Chain Rule is crucial for finding derivatives when the function involves a power of another function.
- 🧮 Simplifying the expression after finding the first derivative can make finding the second derivative easier.
- 📉 When applying the Quotient Rule, it's important to simplify the expression to avoid unnecessary complexity.
- 🔄 The Product Rule is used when differentiating a product of two functions, and it involves multiplying the derivative of one by the other and vice versa.
- ⚙️ Practice algebraic manipulation of the first derivative to simplify the process of finding higher order derivatives.
- 📝 For higher order derivatives beyond the second, you take the derivative of the previous order derivative (e.g., third derivative is the derivative of the second derivative).
Q & A
What is the main topic of section 9.8?
-The main topic of section 9.8 is higher order derivatives.
What is the motivation behind studying higher order derivatives?
-The motivation is that functions that can be derived more than once, such as x cubed, can have their derivatives derived multiple times, and higher order derivatives allow us to denote and work with these repeated derivatives.
How is the second derivative of a function denoted?
-The second derivative is denoted by adding two tick marks above the derivative symbol, like 'y'' or 'f''.
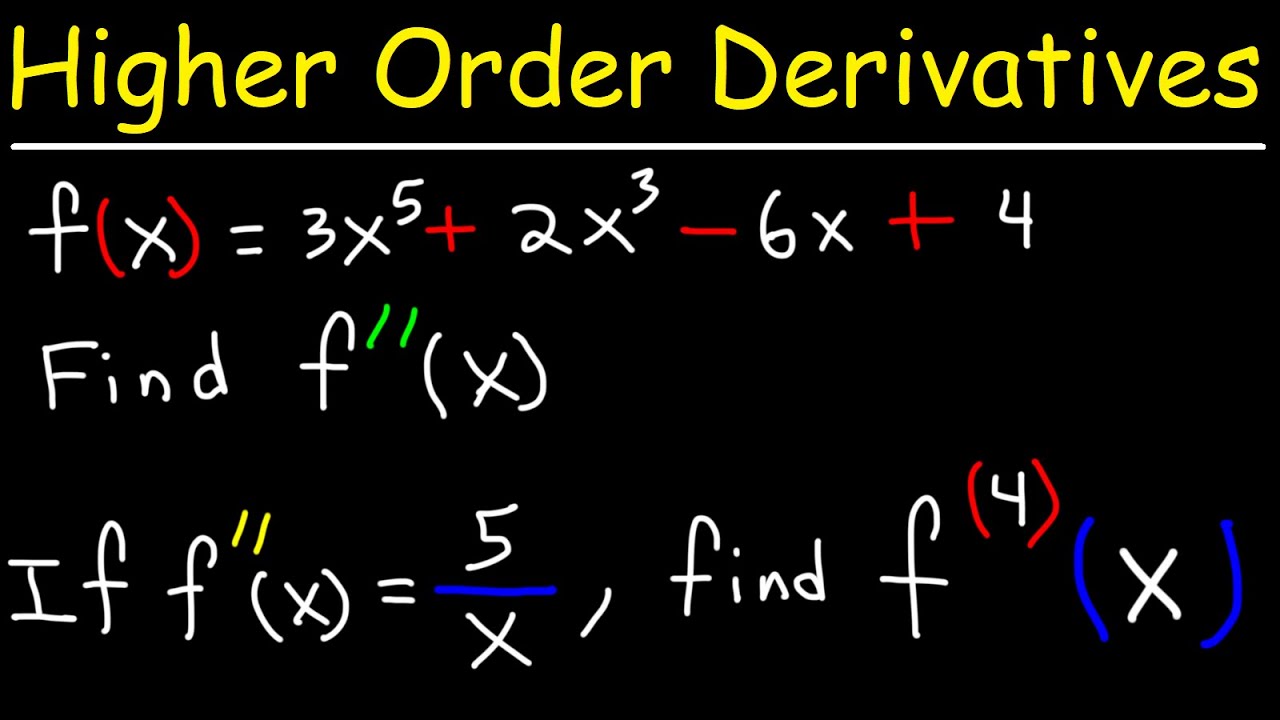
What is the derivative of x cubed?
-The derivative of x cubed is 3x squared.
How can you find the second derivative of a function?
-You can find the second derivative by taking the derivative of the first derivative.
What is the derivative of zero?
-The derivative of zero is zero.
What is the chain rule and how is it applied?
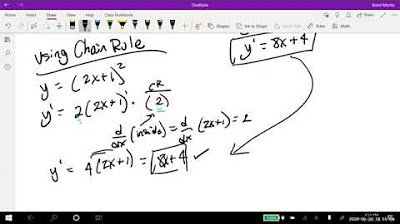
-The chain rule is a method used to find the derivative of a composite function. It states that the derivative of the composite function is the derivative of the outer function times the derivative of the inner function.
What is the quotient rule and how is it used?
-The quotient rule is used to find the derivative of a function that is the quotient of two other functions. It states that the derivative of the quotient is the denominator times the derivative of the numerator minus the numerator times the derivative of the denominator, all divided by the square of the denominator.
What is the purpose of simplifying the first derivative before finding the second derivative?
-Simplifying the first derivative makes it easier to find the second derivative by reducing the complexity of the expression and making the application of the derivative rules more straightforward.
How can you denote the nth derivative of a function?
-The nth derivative of a function can be denoted by placing a small parenthesis with the number 'n' next to the function, like 'y(n)' or 'f^(n)'.
What is the process for finding the third derivative of a function?
-To find the third derivative, you first find the first derivative, then the second derivative, and finally, you take the derivative of the second derivative.
Why is algebraic manipulation of the first derivative important?
-Algebraic manipulation of the first derivative is important because it simplifies the expression, making it easier to apply the derivative rules and find higher order derivatives.
Outlines
📚 Introduction to Higher Order Derivatives
The video begins with an introduction to section 9.8, which focuses on higher order derivatives. The speaker explains that derivatives can be found for functions like x cubed and that these derivatives can be taken multiple times. The notation for higher order derivatives is introduced, with the use of tick marks and parentheses to denote the order of the derivative. The concept of deriving a function infinitely many times is also mentioned, with the derivative of zero always being zero. The video then transitions into examples using the notation f prime, f double prime, and so on, for original functions.
🧮 Applying the Product and Chain Rules
The speaker presents an example problem involving the function f(x) = 3(2 - x)^3. The process of finding the first and second derivatives using the product and chain rules is detailed. The importance of simplifying expressions before taking further derivatives is emphasized. The speaker demonstrates how to apply the product rule by breaking down the derivative into parts and then combining them after applying the rule. The video also shows how to simplify the expression further by factoring out common terms and distributing where necessary.
🔢 Deriving Quotients and Simplifying Algebraically
The third paragraph deals with the quotient rule for derivatives, demonstrated through the function g(x) = (1 - 4x) / (x - 3). The speaker calculates the first derivative and then simplifies the expression algebraically. The process of finding the second derivative is also shown, again using the quotient rule and then simplifying. The video emphasizes the importance of algebraic simplification before taking subsequent derivatives, as it makes the process more manageable. The speaker concludes with a note on the monotony of the process but encourages practice for better understanding and efficiency in finding higher order derivatives.
Mindmap
Keywords
💡Derivative
💡Higher Order Derivatives
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Simplifying
💡Infinitely Derivable
💡Tick Mark Notation
💡F Prime, F Double Prime, etc.
💡Algebraic Manipulation
💡Function Behavior
Highlights
Introduction to higher order derivatives in section 9.8, emphasizing the possibility of deriving functions more than once.
Explanation of denoting higher order derivatives with additional tick marks or using parentheses to indicate the order.
Demonstration of deriving a simple function, x cubed, to show how derivatives can be found successively.
Use of the chain rule in deriving composite functions, as illustrated with an example involving (2 - x) cubed.
Simplification techniques for derived expressions, including the product and chain rules, to make further derivations more manageable.
The concept that the derivative of zero is simply zero, and how it applies to higher order derivatives.
Alternative notation using function names (e.g., f, g) with primes to denote successive derivatives.
Example problem involving the function f(x) = 3(2 - x) cubed, showcasing the application of the chain rule.
Strategy for simplifying expressions before taking successive derivatives to avoid complex calculations.
Illustration of the quotient rule in finding the derivative of a function g(x) = (1 - 4x) / (x - 3).
Technique for algebraically simplifying the first derivative to facilitate the calculation of the second derivative.
Use of the chain rule to find the second derivative of g(x), and the importance of recognizing simplification opportunities.
Emphasis on the algebraic simplification as a key step in preparing for higher order derivative calculations.
The monotonous nature of the section, which is focused on practicing the process of finding successive derivatives.
Advice on expecting to perform algebraic simplification and multiple derivations when tackling problems in this section.
Promise of more video content covering additional example problems to reinforce the concepts of higher order derivatives.
Summary of the process: find the first derivative, simplify, and then continue to derive until the desired order is reached.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: