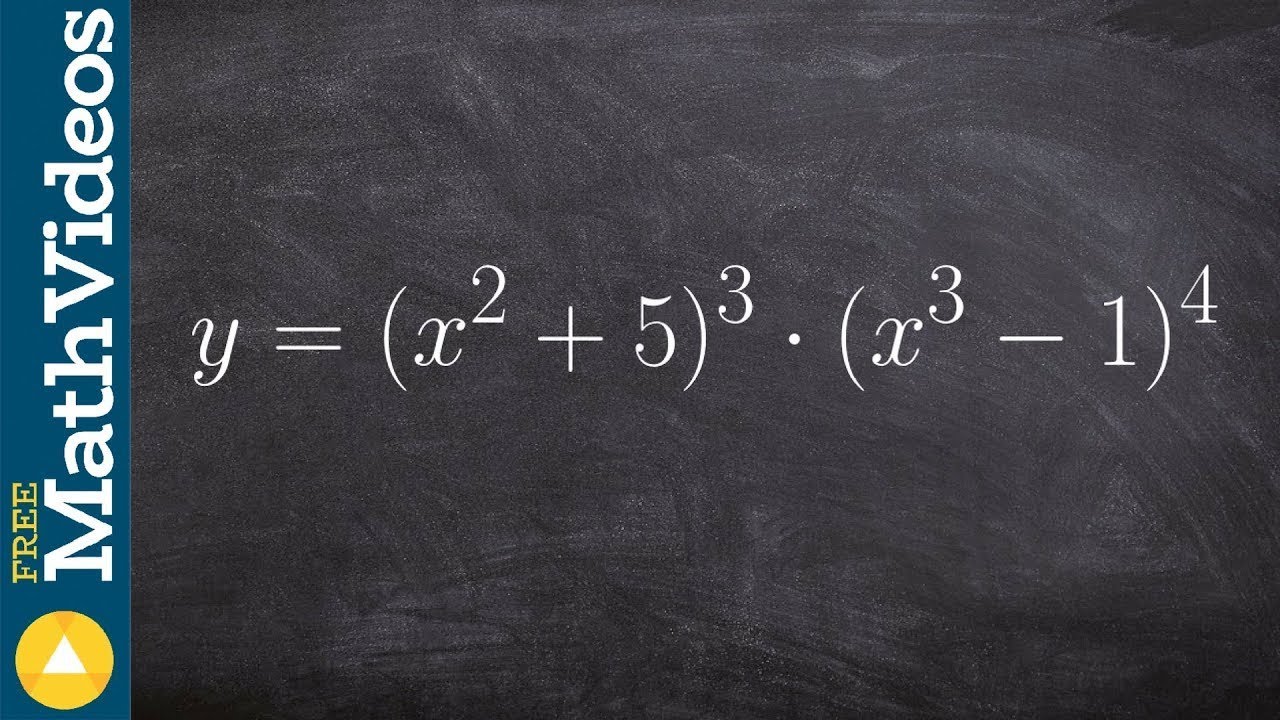How to take the derivative with chain rule inside product rule

Brian McLogan
17 Oct 201704:37
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the application of the product and chain rules in calculus to differentiate a given function. The function consists of a product of two terms: x squared and (x cubed - 4). The presenter guides through the differentiation process step by step, emphasizing the importance of using parentheses for clarity. After applying the product rule, the derivative is simplified by combining like terms and factoring out common factors, such as 6 and (2x + 5) squared. The presenter also suggests simplifying each term first and arranging them in descending order before factoring out the greatest common factor (GCF). The final simplified form of the derivative is presented, and the presenter invites questions or feedback from the audience, ensuring understanding and engagement.

Takeaways
  • 📚 Apply the product rule when differentiating a function that is a product of two functions.
  • 🔗 Recognize the chain rule when dealing with a binomial expression raised to a power.
  • 📐 Differentiate the 'outside' function first, then the 'inside' function in a composite function scenario.
  • ✅ Remember to use parentheses to avoid confusion when differentiating complex expressions.
  • 🧮 Simplify each term after differentiation and arrange them in descending order for clarity.
  • 🔑 Factor out the greatest common factor (GCF) from the differentiated terms to simplify the expression further.
  • 🔢 Treat monomial terms separately from binomial terms when simplifying, as they have different methods of simplification.
  • 📉 Identify and factor out the highest power term from binomial expressions to streamline the simplification process.
  • 🏁 Use brackets to distinguish between terms and groupings in the simplified expression for better readability.
  • 💡 Any term raised to the power of zero is equal to 1, which can be omitted in the final expression unless clarity is needed.
  • ❗ Remember that the final answer should be in a form that would be expected in a multiple-choice test setting, simplified and factored as much as possible.
Q & A

  • What mathematical rule is mentioned at the beginning of the transcript?

    -The product rule is mentioned at the beginning of the transcript.

  • Which function is identified as the parent function in the given example?

    -The parent function identified is x squared (x^2).

  • What is the inside function in the derivative calculation?

    -The inside function is x cubed minus 4 (x^3 - 4).

  • What is the derivative of the parent function x squared?

    -The derivative of the parent function x squared is 2x.

  • What is the derivative of the inside function x cubed minus 4?

    -The derivative of the inside function x cubed minus 4 is 3x^2.

  • How does the speaker suggest to simplify the derivative expression?

    -The speaker suggests simplifying each term first and then arranging them in descending order.

  • What is the common factor that can be factored out from the monomial terms?

    -The common factor that can be factored out from the monomial terms is 6.

  • What term is suggested to be factored out from the binomial terms?

    -The term 2x + 5 squared is suggested to be factored out from the binomial terms.

  • What does anything raised to the power of 0 equal?

    -Anything raised to the power of 0 equals 1.

  • What is the final form of the derivative after factoring out common terms?

    -The final form of the derivative after factoring out common terms is 6(x^2 + (2x + 5)^1 + (x^3 - 4)^1 + (2x + 5)^4).

  • Why does the speaker recommend using parentheses when dealing with complex expressions?

    -The speaker recommends using parentheses to avoid confusion and to clearly indicate the grouping of terms in complex expressions.

  • What is the purpose of the practice of simplifying and factoring out terms in derivatives?

    -The purpose is to make the derivative expression more manageable and to prepare it for further analysis or to match it with the format expected in a multiple-choice question.

Outlines
00:00
📚 Applying the Product and Chain Rules

The paragraph begins with an emphasis on the importance of recognizing the application of the product rule and the chain rule in calculus. The speaker introduces a mathematical expression involving a binomial raised to a higher power, which prompts the use of the chain rule. The explanation continues with a step-by-step process of differentiating the given function, which includes taking derivatives of the terms and applying the product rule. The speaker also emphasizes the use of parentheses to avoid confusion. The process concludes with the derivative of the function, which is then simplified by combining like terms and factoring out the greatest common factor (GCF). The paragraph ends with an invitation for the audience to identify any mistakes or ask questions.

Mindmap
Keywords
💡Product Rule
The Product Rule is a fundamental theorem in calculus used to find the derivative of a product of two functions. In the video, it is applied to a mathematical expression involving two functions, x^2 and x^3 - 4, to find their combined derivative. The rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
💡Chain Rule
The Chain Rule is a method in calculus for finding the derivative of a composite function. It is mentioned in the script when discussing a binomial expression raised to a higher power. The rule is used to break down the derivative into a product of the derivative of the outer function and the inner function. In the video, it is applied to simplify the expression involving x^3 - 4.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. The script focuses on finding derivatives of given functions, which is central to the theme of the video. For instance, the derivative of x^2 is 2x, and this concept is repeatedly used to simplify and find the derivative of more complex expressions.
💡Binomial
A binomial is a polynomial with two terms, such as 'x + 5' or '2x - 4'. In the video, binomials are raised to powers and manipulated using the Chain Rule and other algebraic techniques. The script discusses binomials in the context of derivatives and simplification, which is essential for understanding the overall process of differentiating expressions.
💡Simplifying
Simplification in mathematics involves reducing complex expressions to a more straightforward form. The script emphasizes the importance of simplifying expressions after applying the Product and Chain Rules. This process helps in organizing terms and finding a more manageable form of the derivative, which is crucial for further analysis or for multiple-choice questions.
💡Monomial
A monomial is an algebraic expression with only one term, such as '3x' or '4y^2'. In the video, monomials are discussed in the context of simplifying expressions. They are often the simplest form of terms that result from the differentiation process and are easier to manipulate and combine with other terms.
💡Factoring Out
Factoring out is the process of extracting the greatest common factor (GCF) from a polynomial. In the script, this technique is used to simplify expressions further by identifying common factors across terms. Factoring out '6' from certain terms is an example from the video, which helps in reducing the complexity of the expression.
💡
💡Greatest Common Factor (GCF)
The GCF is the largest factor that two or more numbers have in common. In the context of the video, finding the GCF is a step towards simplifying algebraic expressions. It is used to factor out common terms from a polynomial, which simplifies the expression and makes it easier to work with.
💡Parentheses and Brackets
Parentheses and brackets are mathematical symbols used to group terms or expressions in an equation. In the video, they are used to clarify the order of operations and to distinguish between different parts of the expression. The script mentions the importance of using parentheses to avoid confusion, especially when dealing with complex expressions involving multiple operations.
💡Exponents
Exponents are used to indicate the number of times a base is multiplied by itself. In the video, exponents are used in the context of binomials raised to higher powers, which requires the application of the Chain Rule for differentiation. The script discusses how to handle expressions with exponents during the simplification process.
💡Multiple Choice
Multiple choice is a type of question format where respondents are given a question and a set of possible answers, out of which they must choose the correct one. The script mentions that the process of simplifying derivatives, as taught in the video, is not typically seen in the form of multiple-choice questions on tests, implying that the skills taught are more for understanding and application rather than for standardized testing.
Highlights

The transcript discusses the application of the product rule and the chain rule in calculus.

The derivative of the first term is taken, considering the outside and inside functions.

The parent function is x squared, and the inside function is x cubed minus 4.

The derivative of the parent function is 2x, and the derivative of the inside function is 3x.

The importance of using parentheses for clarity in mathematical expressions is emphasized.

The process of simplifying expressions by combining like terms is demonstrated.

The transcript shows how to apply the chain rule to a binomial raised to a higher power.

A step-by-step approach to simplifying derivatives is presented, including factoring out common terms.

The use of brackets is suggested to differentiate between grouping terms and parentheses.

The transcript provides a practical example of how to factor out the greatest common factor (GCF).

The concept of anything raised to the power of 0 being equal to 1 is mentioned.

The final simplified form of the derivative is expressed in terms of x squared, x cubed, and constants.

The transcript encourages the audience to check for mistakes and ask questions for clarification.

The importance of recognizing and applying mathematical rules, such as the product and chain rules, is highlighted.

The transcript illustrates the process of taking derivatives of composite functions.

The use of the product rule is demonstrated with a specific example involving x squared and x cubed minus 4.

The transcript explains the concept of factoring out terms from a derivative to simplify the expression.

The process of simplifying derivatives for a test environment is discussed, where multiple-choice questions are common.

The transcript concludes with a reminder that the goal is to simplify the derivative to a form that would be expected in a test setting.

Transcripts

Browse More Related Video

Taking the derivative of two binomials using product and chain rule

Product Rule With 4 Functions - Derivatives | Calculus

Implicit Differentiation for Calculus - More Examples #2

Simplifying Derivatives

How to use implicit differentiation on an equation for dy dx

Factoring Review

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusProduct RuleChain RuleDerivativeBinomialMathematicsEducationSimplificationFactoringLearningComplex Functions