Derivative of e_____cos(e_) | Advanced derivatives | AP Calculus AB | Khan Academy
TLDRThe video script discusses the application of the product rule and chain rule to derive a complex mathematical expression. It involves taking the derivative of the product of the cosine of x and e to the cosine of x. The explanation is methodical, walking through the process of identifying the two functions, applying the product rule to find their derivatives, and then using the chain rule to evaluate these derivatives. The final result is presented in a simplified form, demonstrating a thorough understanding of calculus concepts.
Takeaways
- 📚 The script discusses the process of differentiating a complex mathematical expression involving the product and chain rules.
- 🌀 The expression in question is the derivative of cosine of x times e to the cosine of x.
- 🔄 The product rule is applied to break down the expression into two parts for easier differentiation.
- 📈 The first part involves the derivative of e to the power of the function 'cosine of x'.
- 📊 For the first part, the outer function's derivative is e to the cosine of x, and it is multiplied by the derivative of the inner function, which is -sine of x.
- 🔄 The second part of the expression requires finding the derivative of the cosine of e to the x with respect to x.
- 📈 The chain rule is used again for the second part, identifying 'e to the x' as the inner function and 'cosine' as the outer function.
- 📊 The derivative of the outer function with respect to 'e to the x' is -sine of 'e to the x', and it is multiplied by the derivative of 'e to the x', which is simply 'e to the x'.
- 🔢 The final derivative expression is a combination of both parts, resulting in a product of several terms involving e to the power of x and sine of x.
- 🔍 The final expression can be simplified by combining like terms, but the script leaves it in its expanded form for clarity.
- 🎓 The process demonstrated in the script is an example of applying fundamental calculus rules to solve for derivatives of complex functions.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is the process of finding the derivative of a specific mathematical expression using the product rule and the chain rule.
What is the expression for which the derivative is being found?
-The expression for which the derivative is being found is the cosine of x times the exponential function e to the cosine of x.
What is the product rule mentioned in the transcript?
-The product rule is a calculus formula used to find the derivative of the product of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
How is the chain rule applied in this context?
-The chain rule is applied to find the derivatives of the individual functions within the product rule. It is used to evaluate the derivative of the exponential function with respect to the cosine of x and the derivative of the cosine function with respect to the exponential function.
What is the derivative of the outer function e to the something with respect to something?
-The derivative of the outer function e to the something with respect to something is simply e to the something, which in this case is e to the cosine of x.
What is the derivative of the cosine function with respect to x?
-The derivative of the cosine function with respect to x is negative sine of x.
What is the final expression for the derivative of the given expression?
-The final expression for the derivative is negative e to the cosine of x times e to the x times sine of e to the x times sine of x plus e to the cosine of x times the derivative of the second function.
How can the final expression be simplified?
-The final expression can be simplified by factoring out common terms such as e to the x and e to the cosine of x, and by combining like terms.
What is the significance of using both the product rule and the chain rule in this problem?
-The significance of using both the product rule and the chain rule in this problem is that it demonstrates a method for finding the derivative of complex expressions that involve the product of functions and the evaluation of derivatives with respect to composite functions.
What is the role of the sine function in the final derivative expression?
-The sine function appears in the final derivative expression as a factor that multiplies with the exponential functions, indicating the influence of the sine of x on the rate of change of the original expression.
How does the process outlined in the transcript help in understanding calculus concepts?
-The process outlined in the transcript helps in understanding calculus concepts by demonstrating the step-by-step application of the product rule and the chain rule, which are fundamental tools in differentiating complex functions.
Outlines
🧮 Deriving a Complex Expression Using Product and Chain Rules
This section delves into the derivative of a complex expression, e^(cos(x)) * cos(e^x), employing both the product and chain rules for differentiation. The expression is broken down as the product of two functions, necessitating the use of the product rule initially to separate the derivatives. It is explained how each derivative is then tackled individually using the chain rule. For the first function, e^(cos(x)), the derivative is obtained by applying the chain rule, resulting in e^(cos(x)) * (-sin(x)). For the second function, cos(e^x), again the chain rule applies, yielding -sin(e^x) * e^x. The segment meticulously illustrates the step-by-step application of these rules, reinforcing the interplay between the product and chain rules in calculus.
🔚 Finalizing the Derivation with Simplification
The conclusion of the derivative's derivation simplifies the previously obtained expressions. It revisits the application of the product and chain rules, culminating in a neat simplification of the complex expression's derivative. Specifically, it highlights the assembly of the derived components into the final expression, accentuating the negative sign's placement and the multiplication of e^x with e^(cos(x)) as key steps. This segment is pivotal for demonstrating how to neatly integrate and simplify the parts of a derivative calculation, showcasing the culmination of applying calculus rules to a complex expression.
Mindmap
Keywords
💡Derivative
💡Chain Rule
💡Product Rule
💡Cosine
💡Exponential Function
💡Sine
💡Differentiation
💡Rate of Change
💡Composite Function
💡Trigonometric Functions
💡Mathematical Analysis
Highlights
Introduction to differentiating a complex expression involving e to the power of cosine of x times cosine of e to the x.
Explanation of viewing the expression as a product of two functions, applying the product rule.
Derivation starts with differentiating e to the cosine of x, introducing the chain rule for further steps.
Identification of the outer function as e to something, leading to e to the cosine of x after differentiation.
Multiplication by the derivative of the inner function, cosine of x, results in negative sine of x.
Complete derivation of the first term using the chain rule, highlighting the product of derivatives.
Transition to differentiating the second function, cosine of e to the x, with anticipation of applying the chain rule again.
Explanation of the derivative of cosine of something as negative sine of that something, in this context, e to the x.
Multiplication by the derivative of e to the x with respect to x, which is just e to the x.
Finalization of the derivative of the second function, showcasing the application of the chain rule.
Substitution of the derived terms back into the original product rule expression.
Simplification and rearrangement of terms for clarity and coherence in the final derivative expression.
Illustration of how to combine terms with the same base during simplification, despite leaving it in expanded form.
Completion of the derivative, summarizing the application of both the product and chain rules on a complex expression.
Emphasis on the systematic approach to differentiation, demonstrating the power of combining algebraic and calculus concepts.
Transcripts
Browse More Related Video

Simplifying Derivatives

Product Rule With 4 Functions - Derivatives | Calculus
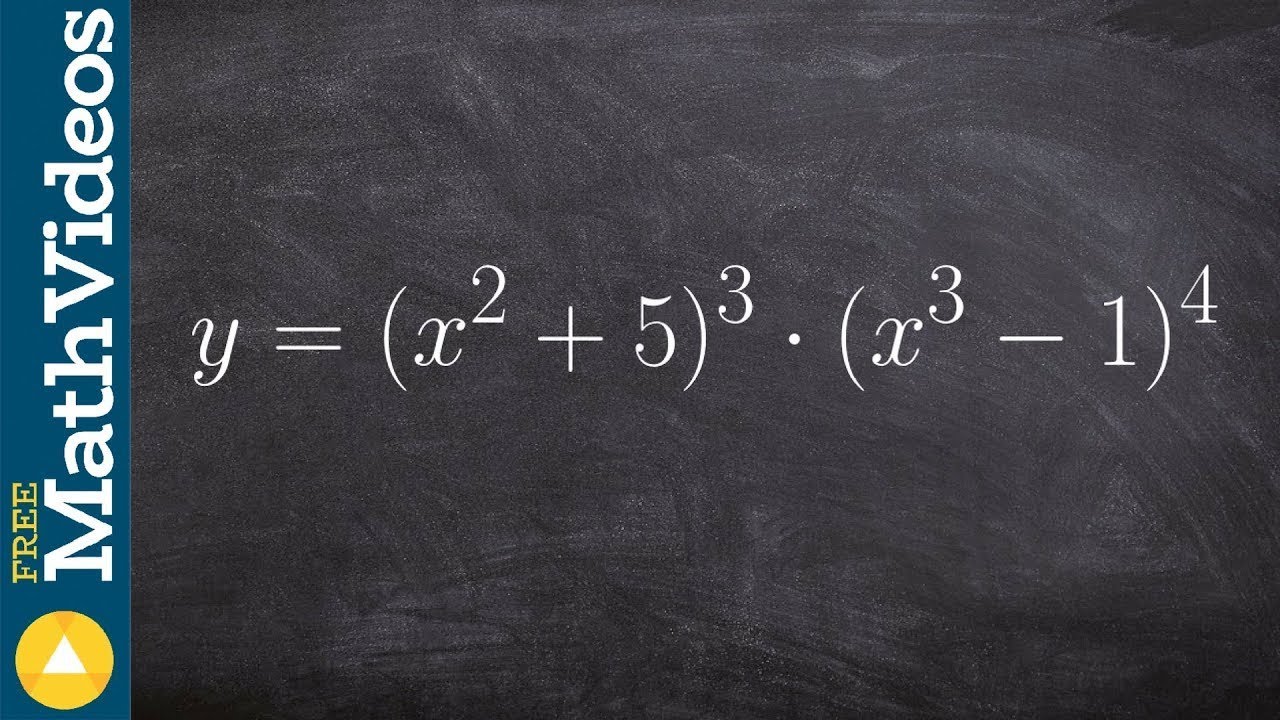
Taking the derivative of two binomials using product and chain rule

The Chain Rule - More Examples

Logarithmic functions differentiation | Advanced derivatives | AP Calculus AB | Khan Academy

BusCalc 11 Derivative Product Rule
5.0 / 5 (0 votes)
Thanks for rating: