The Chain Rule
TLDRThe video script provides an in-depth lesson on the Chain Rule, a fundamental concept in calculus for differentiating composite functions. The instructor begins by explaining the concept of composite functions, denoted as f(G(x)) or F(G of X), where f(x) is the outer function and G(x) is the inner function. The Chain Rule is then introduced as a method to find the derivative of such compositions. The process involves differentiating the outer function while treating the inner function as a single variable (often replaced with 'u'), and then multiplying by the derivative of the inner function. The lesson continues with step-by-step examples, illustrating how to apply the Chain Rule to various functions, including those requiring the use of additional differentiation rules such as the power rule and the quotient rule. The instructor also demonstrates how to simplify expressions and emphasizes the importance of practice to master the technique. The script concludes with a comprehensive example that involves finding the derivative at a specific point, calculating the slope of the tangent line, and writing the equation of the tangent line using the point-slope form. The lesson is practical, emphasizing the application of the Chain Rule to solve complex differentiation problems.
Takeaways
- ๐ The Chain Rule is a fundamental differentiation technique used to find the derivative of compositions of functions.
- ๐ In a composition of functions, the outer function is the one into which the inner function (G(x)) is plugged in to form F(G(x)).
- ๐ฏ To apply the Chain Rule, first differentiate the outer function with respect to the inner function, then multiply by the derivative of the inner function.
- ๐ The Chain Rule simplifies the process of differentiating complex functions, especially when dealing with high powers or nested functions.
- โ๏ธ The process often involves substituting the inner function with a new variable (u), finding the derivative with respect to that variable, and then substituting back.
- ๐งฎ Practice is key to mastering the Chain Rule, as it allows for shortcuts and mental calculations that bypass the need for explicit substitution steps.
- ๐ The Chain Rule is not only limited to polynomial functions but also applies to more complex scenarios such as rational functions and square roots.
- ๐ค Recognizing the outer and inner functions is crucial for applying the Chain Rule correctly and differentiating composite functions.
- ๐ When differentiating more complex composite functions, it may be necessary to use additional rules like the Quotient Rule or Product Rule in conjunction with the Chain Rule.
- ๐ The final form of the derivative can often be simplified further, and it's important to express the derivative in its most concise and understandable form.
- ๐ The Chain Rule is a powerful tool that, when combined with other differentiation rules, can tackle a wide array of calculus problems involving composite functions.
Q & A
What is the Chain Rule in calculus?
-The Chain Rule is a differentiation rule used to find the derivative of compositions of functions. It states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function.
How do you denote the composition of two functions, f and g, in calculus?
-The composition of two functions f and g can be denoted in two ways: as fโg or f(g(x)). Both notations are read as 'F of G of X'.
What is the outer function in a composition of functions?
-In a composition of functions, the outer function is the function that the inner function is plugged into. It is also sometimes referred to as the parent function.
What is the inner function in a composition of functions?
-The inner function in a composition is the function that gets plugged into the outer function. It is also sometimes called the transformation of the parent function.
How does the Chain Rule simplify the process of differentiating complex functions?
-The Chain Rule simplifies the differentiation process by allowing you to differentiate the outer function while treating the inner function as a single entity, and then multiply by the derivative of the inner function. This avoids the need to expand and differentiate each term of a complex function individually.
What is the general formula for the Chain Rule?
-The general formula for the Chain Rule is (d/dx)[f(g(x))] = f'(g(x)) * g'(x), where f'(g(x)) is the derivative of the outer function evaluated at the inner function, and g'(x) is the derivative of the inner function.
How do you apply the Chain Rule to a function like y = โ(x - 7)?
-First, rewrite the function with an exponent: y = (x - 7)^(1/2). Then, let u = x - 7, so y = u^(1/2). Apply the Chain Rule: dy/dx = (1/2)u^(-1/2) * du/dx, where du/dx = 1. Thus, dy/dx = (1/2)(x - 7)^(-1/2) * 1 = (1/2โ(x - 7)).
What is the Quotient Rule in calculus, and how is it different from the Chain Rule?
-The Quotient Rule is used to differentiate quotients of two functions. It states that the derivative of the quotient f(x)/g(x) is [g(x)f'(x) - f(x)g'(x)] / [g(x)]^2. The Chain Rule, on the other hand, is used for differentiating compositions of functions. The main difference is that the Quotient Rule deals with division, while the Chain Rule deals with nested functions.
Can you provide an example of using the Chain Rule to find the derivative of y = (2x - 5)^(5/3)?
-Let u = 2x - 5, so y = u^(5/3). By the Chain Rule, dy/dx = (5/3)u^(2/3) * du/dx. Calculate du/dx = 2. The derivative is then (5/3)(2x - 5)^(2/3) * 2 = (10/3)(2x - 5)^(2/3).
What is the process for finding the equation of a tangent line to a curve at a specific point using the Chain Rule?
-First, find the derivative of the curve using the Chain Rule. Then, evaluate the derivative at the specific point to find the slope of the tangent line. Next, find the y-coordinate of the point on the curve by substituting the x-value into the original function. Finally, use the point-slope form of a line to write the equation of the tangent line.
Why is it important to practice differentiating functions using the Chain Rule, even if you can do it without it in simple cases?
-Practicing the Chain Rule is important because it is essential for differentiating more complex functions that cannot be easily handled without it. It's a fundamental skill in calculus that allows for the simplification and efficient computation of derivatives in various mathematical and real-world applications.
Outlines
๐ Introduction to the Chain Rule
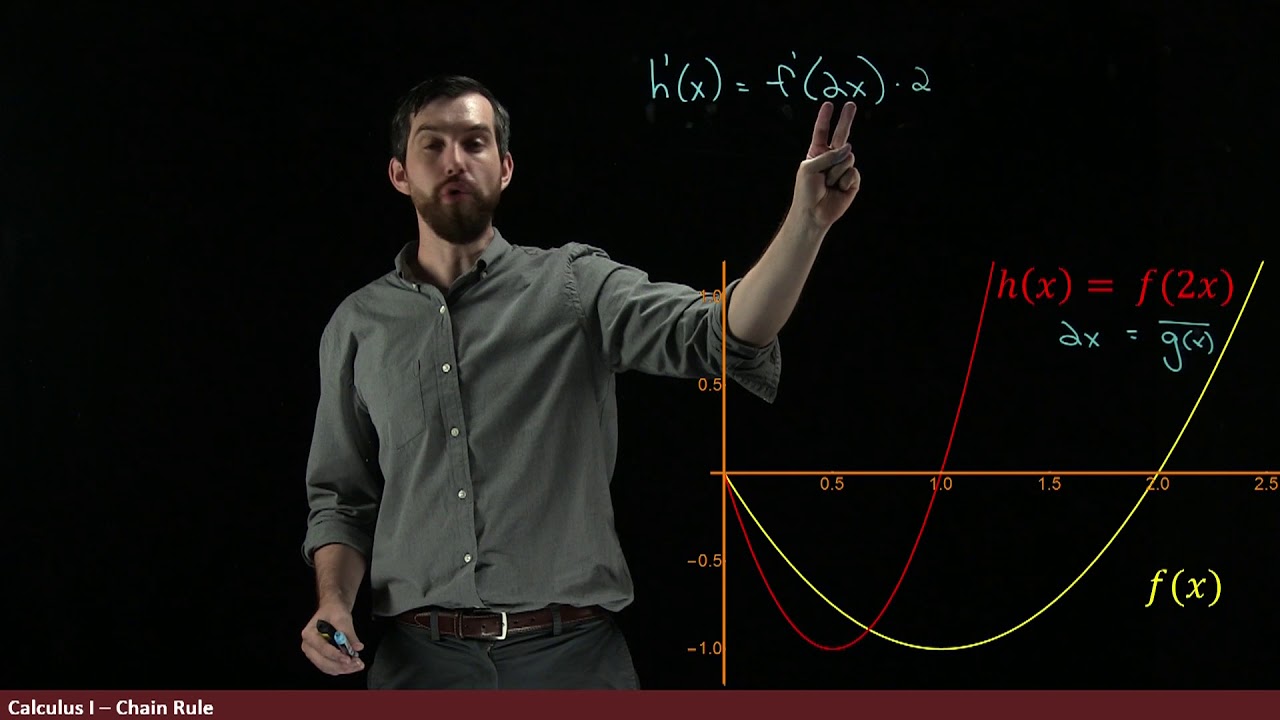
The paragraph introduces the Chain Rule, a fundamental concept in calculus for differentiating compositions of functions. It explains the notation for composite functions and distinguishes between the outer (parent) function and the inner (transformation) function. The importance of the Chain Rule is highlighted, especially for differentiating complex functions without the need for extensive manual expansion.
๐ข Applying the Chain Rule
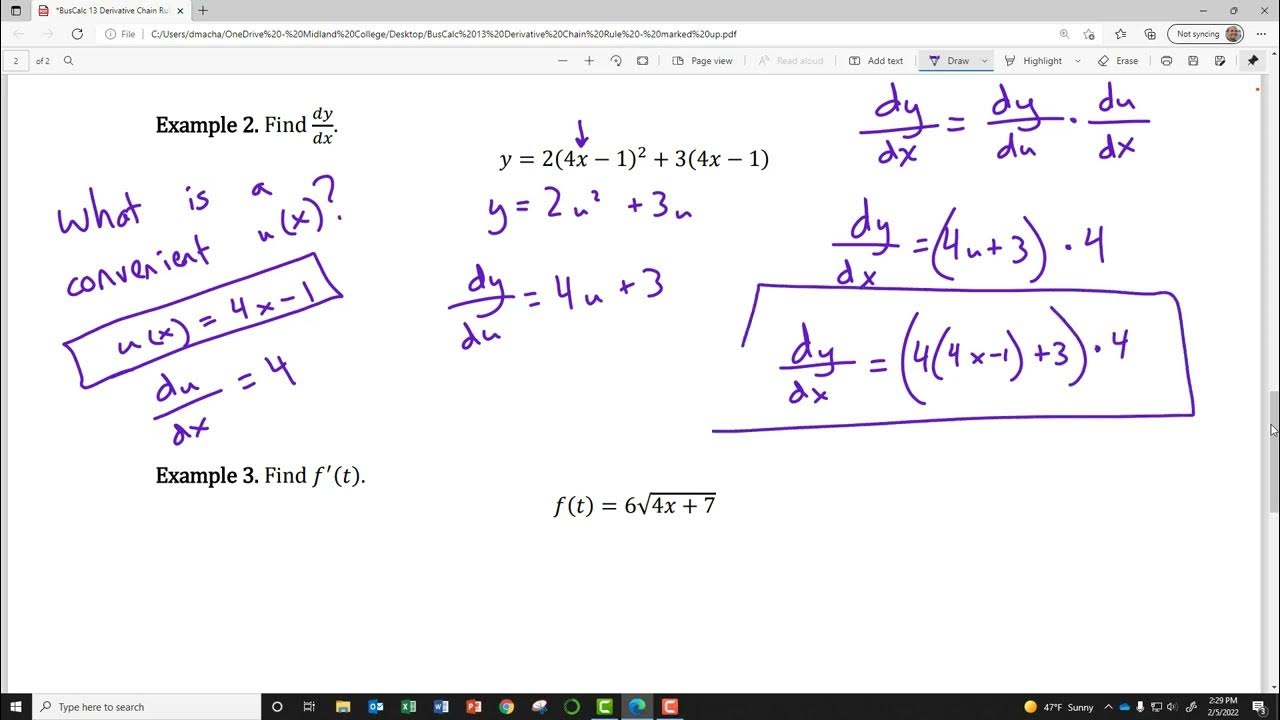
This section delves into the application of the Chain Rule, illustrating the process with examples. It outlines the steps for differentiating composite functions by first finding the derivative of the outer function, then multiplying by the derivative of the inner function. The paragraph emphasizes the technique of substituting the inner function with a variable (u-substitution) to simplify the differentiation process.
๐ Simplifying the Chain Rule Process
The paragraph focuses on simplifying the application of the Chain Rule by avoiding unnecessary steps. It demonstrates how to directly apply the rule without intermediate substitution steps, showing that with practice, the process becomes more intuitive and efficient. The paragraph also includes an example of differentiating a square root function using the Chain Rule.
๐ Advanced Chain Rule Applications
This part of the script explores more complex applications of the Chain Rule, including situations where the inner function requires the use of the quotient rule. The paragraph demonstrates the process of differentiating more complicated functions, emphasizing the importance of correctly applying the Chain Rule and the quotient rule when necessary.
๐ Derivative at a Specific Point
The focus shifts to finding the derivative at a specific point, rather than the general derivative. The paragraph explains how to find the slope of the tangent line at a given x-value by substituting into the derivative. It also covers finding the y-coordinate of the point of tangency by evaluating the original function at the given x-value.
๐ Writing the Equation of the Tangent Line
The final paragraph describes the process of writing the equation of the tangent line to the curve at a specific point. It uses the point-slope form of a line to express the equation, substituting the slope found from the derivative and the coordinates of the point of tangency. The paragraph concludes with the verification of the derived equation using a graphing tool like Desmos.
๐ฃ๏ธ Conclusion and Offer for Help
The script concludes with an offer for further assistance and an encouragement to reach out if additional help is needed. It acknowledges the complexity of the algebra involved in the problems and provides reassurance that the presenter is available for support.
Mindmap
Keywords
๐กChain rule
๐กDerivative
๐กComposite functions
๐กOuter function
๐กInner function
๐กPower rule
๐กQuotient rule
๐กProduct rule
๐กTangent line
๐กPoint of tangency
๐กDesmos
Highlights
The Chain Rule is a differentiation rule used to find the derivative of compositions of functions.
Composition of two functions can be denoted as F(G(x)) or (fโg)(x), where F is the outer function and G is the inner function.
The Chain Rule states that the derivative of a composite function y = F(G(x)) is dy/dx = F'(G(x)) * G'(x).
To apply the Chain Rule, first replace the inner function with a new variable, such as u, to simplify differentiation.
After finding the derivative of the outer function with respect to the new variable, substitute back the original inner function.
Multiply the result by the derivative of the inner function to complete the application of the Chain Rule.
The Chain Rule is particularly useful when dealing with complex or higher power compositions that are cumbersome to expand.
An example given was the composition of a linear function (2x - 5) and a quadratic function (x^2), demonstrating how to apply the Chain Rule.
Another example was the composition involving a square root function and a linear function (x - 7), illustrating the identification of inner and outer functions.
A rational function was also used as an example, emphasizing the process of identifying the inner function (x^2 - x - 20) and outer function (1/x).
The Chain Rule simplifies the differentiation process, avoiding the need to expand complex expressions before applying the power rule.
The process of differentiating a composite function using the Chain Rule was demonstrated step by step for clarity.
Shortcuts and mental calculations can be used to simplify the application of the Chain Rule after understanding the process.
The derivative of a composite function can be found without explicitly going through all the substitution steps, once familiar with the rule.
The Chain Rule can be combined with other differentiation rules, such as the power rule and the quotient rule, for more complex functions.
The Chain Rule is not only about finding the derivative but also about identifying the correct outer and inner functions within a composition.
The process of finding a derivative at a specific point and the equation of the tangent line at that point was demonstrated using the Chain Rule.
Transcripts
Browse More Related Video
Chain rule | Derivative rules | AP Calculus AB | Khan Academy
Worked example: Derivative of รยรย(3x_-x) using the chain rule | AP Calculus AB | Khan Academy
Interpreting the Chain Rule Graphically
Derivatives of Composite Functions: The Chain Rule
1.7 - The Chain Rule
BusCalc 13 Derivative Chain Rule
5.0 / 5 (0 votes)
Thanks for rating: