AP Physics Workbook 5.O Conservation of Energy and Momentum
TLDRThis video script delves into the principles of the conservation of energy and momentum in physics, specifically within a scenario involving two carts and a spring. It explains how the total mechanical energy remains constant in a conservative system, and how increasing the mass of the first cart (m1) affects the final velocity and momentum of the system. The script also includes a mathematical derivation that demonstrates the direct proportionality between velocity and the square root of mass, supporting the claim that a larger mass results in a greater final velocity, thus providing a deeper understanding of the physical concepts at play.
Takeaways
- 📚 The script is a tutorial on Unit 5 Momentum from an AP Physics workbook, focusing on the conservation of energy and momentum.
- 🌟 The scenario involves a cart (m1) with spring potential energy that gets compressed and then releases, moving towards and hitting another cart (m2).
- 🔄 The system is conservative, meaning there is no friction, and the total mechanical energy does not change when m1 is large.
- ⚙️ The initial mechanical energy stored in the spring (potential energy) is converted into kinetic energy as m1 moves.
- 📈 The final velocity of cart m1 changes with its mass; as m1 increases, its final velocity decreases, but its momentum may still increase due to conservation of momentum.
- 💡 The total momentum of the system (m1 + m2) will be larger if m1 is larger because momentum is the product of mass and velocity.
- 🚀 To achieve a larger final velocity, m1 should be larger, as it helps to increase the system's momentum while not affecting the total mechanical energy.
- 📊 The conservation of momentum and energy principles are used together to derive an equation that supports the claim that increasing mass leads to an increase in velocity.
- 🔢 The derived equation shows that the velocity is directly proportional to the square root of m1, confirming that increasing mass results in a higher velocity.
- 📝 The process of rationalizing the denominator is mentioned, which is a mathematical technique used to simplify fractions involving square roots.
- 🎓 The script serves as an educational resource for understanding the principles of conservation of energy and momentum in a physical system.
Q & A
What is the main topic of the tutorial?
-The main topic of the tutorial is the conservation of energy and momentum in the context of a physics problem involving two carts, M1 and M2, and a spring.
How does the total mechanical energy of the system change when M1 is launched?
-The total mechanical energy of the system does not change when M1 is launched, as it is a conservative system. The spring's potential energy is converted into the kinetic energy of M1.
What is the role of friction in this scenario?
-Friction is neglected in this scenario, which implies that the system is idealized and energy losses due to friction are not considered.
What happens to the total momentum of the system after M1 is launched?
-The total momentum of the system remains constant after M1 is launched, according to the law of conservation of momentum.
How does the mass of M1 (m1) affect the final velocity of the carts?
-The final velocity of the carts is directly proportional to the square root of the mass of M1. As M1 increases, the final velocity also increases due to the conservation of momentum.
What is the initial form of potential energy in this problem?
-The initial form of potential energy in this problem is spring potential energy, which is then converted into kinetic energy.
What is the significance of the equation m1 * v = constant in the context of this problem?
-The equation m1 * v = constant indicates that the momentum (product of mass and velocity) of M1 is conserved throughout the interaction with M2.
How does the increase in M1's mass affect the overall momentum of the system?
-An increase in M1's mass results in an increase in the overall momentum of the system, provided that the velocity of M1 decreases proportionally less than the increase in mass.
What mathematical concept is used to derive the relationship between mass and velocity?
-The mathematical concept used to derive the relationship between mass and velocity is the conservation of momentum, combined with the concept of rationalizing the denominator when dealing with square roots in fractions.
What is the final conclusion regarding M1's mass and the velocity of the carts?
-The final conclusion is that increasing M1's mass will result in an increase in the final velocity of the carts, due to the conservation of momentum and the direct proportionality between velocity and the square root of mass.
How does this tutorial relate to the principles of the AP Physics exam?
-This tutorial relates to the principles of the AP Physics exam by demonstrating the application of fundamental concepts such as conservation of energy and momentum in solving physics problems, which are key topics in the AP Physics curriculum.
Outlines
📚 Introduction to Unit 5: Momentum and Conservation Laws
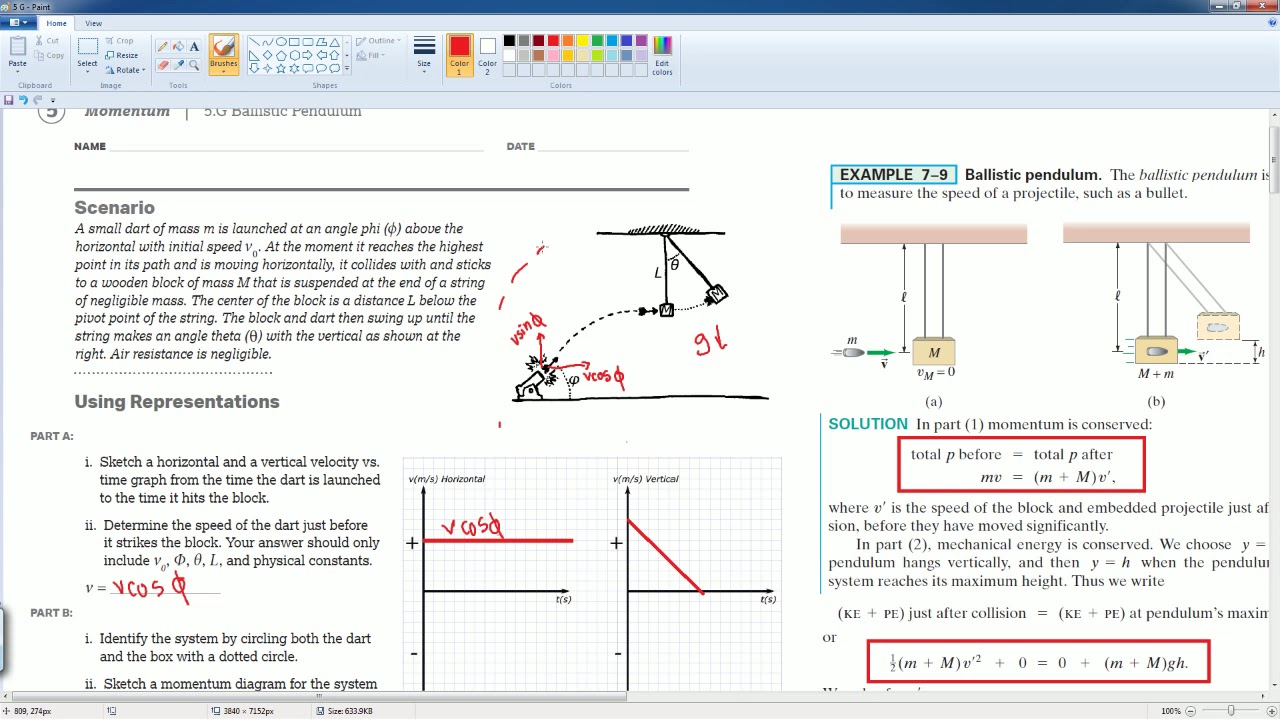
This paragraph introduces the topic of the video, which is Unit 5 of an AP Physics workbook focusing on momentum. It sets the scene for the discussion by describing a scenario where a car (m1) is compressed, gaining spring potential energy, and then releases this energy to move towards and collide with another car (m2). The paragraph outlines the task of breaking down the claim and evidence regarding the conservation of energy and momentum in a system without friction. It also begins to address the question of how the total mechanical energy of the system changes after cart 1 is launched and provides an initial analysis based on the conservation of energy, stating that the total mechanical energy remains constant in a conservative system.
🚀 Analysis of Momentum and Velocity with Varying Mass
The second paragraph delves deeper into the analysis of how the total momentum of the system changes when the mass of m1 is large. It explains the conservation of momentum and how it relates to the system's velocity. The paragraph clarifies that while the mass of m1 increases, its velocity may decrease, the momentum could still increase due to the larger mass. This is because momentum is the product of mass and velocity, and an increase in mass can compensate for a decrease in velocity, maintaining or even increasing the momentum. The paragraph also discusses the implications of increasing m1 to achieve a larger final velocity (v) and provides a mathematical derivation to support this claim. By combining the principles of conservation of energy and momentum, the paragraph derives an equation that shows the final velocity is directly proportional to the square root of m1. This confirms that increasing the mass (m1) will result in an increase in velocity, thus supporting the claim that m1 should be large to achieve a higher final speed.
Mindmap
Keywords
💡Conservation of Energy
💡Momentum
💡Mechanical Energy
💡Conservative System
💡Spring Potential Energy
💡Kinetic Energy
💡Collision
💡Velocity
💡Mass
💡Conservation of Momentum
💡Direct Proportion
Highlights
The topic of discussion is the conservation of energy and momentum in a physics scenario involving two carts and a spring.
The first cart (m1) is compressed and releases spring potential energy, moving towards and hitting the second cart (m2).
The system is conservative, meaning there is no friction or external forces affecting the total mechanical energy.
The total mechanical energy of the system remains constant despite changes in mass or velocity.
The initial potential energy stored in the spring is converted into kinetic energy for the carts.
The final velocity of cart m1 changes with its mass; as m1 increases, its final velocity decreases.
The total momentum of the system is conserved and is dependent on both the masses and velocities of the carts.
Increasing the mass of m1 (while keeping the system conservative) results in a larger total momentum.
The final velocity of the carts is directly proportional to the square root of the mass of m1.
The mathematical derivation involves both conservation of energy and conservation of momentum principles.
The equation derived from the conservation laws shows that increasing m1 will increase the velocity of the system.
The process of rationalizing the denominator is mentioned as a mathematical technique used in the derivation.
The final equation supports the claim that the velocity is directly proportional to the square root of the mass of m1.
The analysis concludes that m1 should be large to achieve a high final velocity in the system.
The tutorial provides a comprehensive understanding of the physics concepts applied to the scenario.
The transcript is a valuable resource for learning the application of conservation laws in physics problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: