AP Physics Workbook 5.G Ballistic Pendulum
TLDRThis tutorial delves into solving the Ballistic Pendulum Problem from the AP Physics workbook, emphasizing the conservation of momentum and mechanical energy. It explains how to sketch velocity vs. time graphs, calculate the system's collision velocity and final height using equations derived from these principles. The tutorial also illustrates the impact of increasing the dart's mass on both the collision velocity and the height gained, providing a deeper understanding of the physical concepts involved.
Takeaways
- 📚 The tutorial covers the 'Five Point G - The Ballistic Pendulum Problem' from the AP Physics workbook.
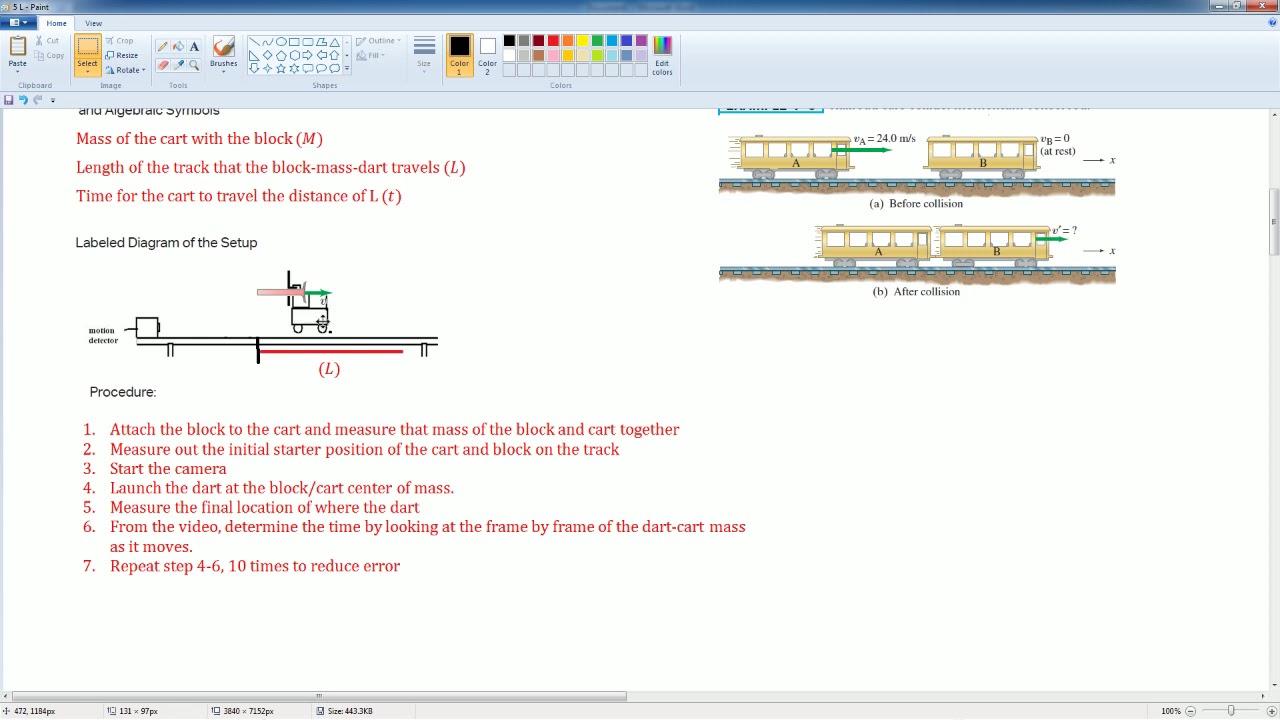
- 🎯 The problem involves a bullet hitting a stationary mass, causing it to lift a certain height, demonstrating conservation of momentum.
- 🔄 The total momentum before the collision (mv) is equal to the total momentum after the collision (m + M)v', where m is the mass of the bullet and M is the mass of the pendulum.
- 🚀 The conservation of mechanical energy in the vertical direction is given by the equation: (1/2)(m + M)v'^2 = h, where h is the height gained.
- 🌟 A key equation provided is v' = √(2gh) for finding the collision velocity, and v = √(2gh) for the original velocity when dividing m by (m + M).
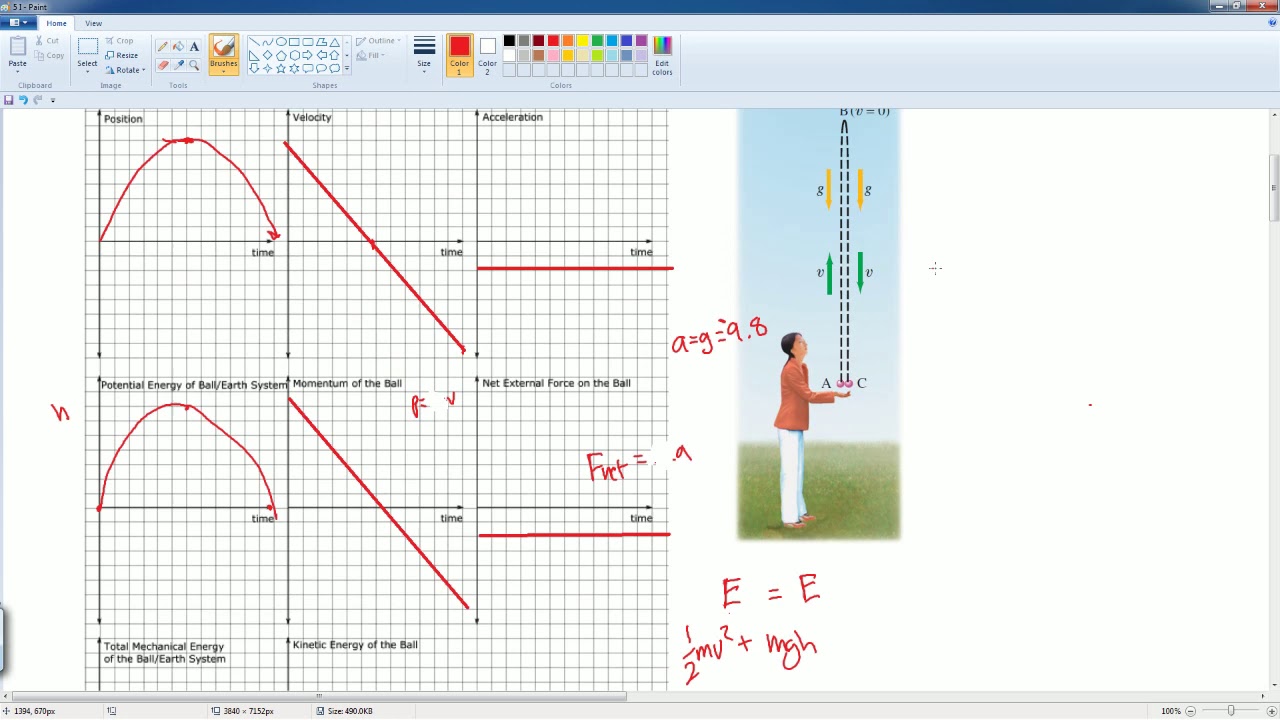
- 📊 The first task is to sketch horizontal and vertical velocity versus time graphs, with the horizontal velocity being constant (v cos θ) and the vertical velocity decreasing over time due to gravity.
- 🎢 The vertical component of the velocity (v sin φ) decreases because gravity acts downwards, affecting the object's upward motion.
- 🥊 Determining the speed of the dart just before it strikes the block involves using the equation v₀ = v cos φ, where v₀ is the initial velocity and φ is the angle.
- 🌐 The system to be considered includes the dart, the block, and the Earth due to gravitational potential energy.
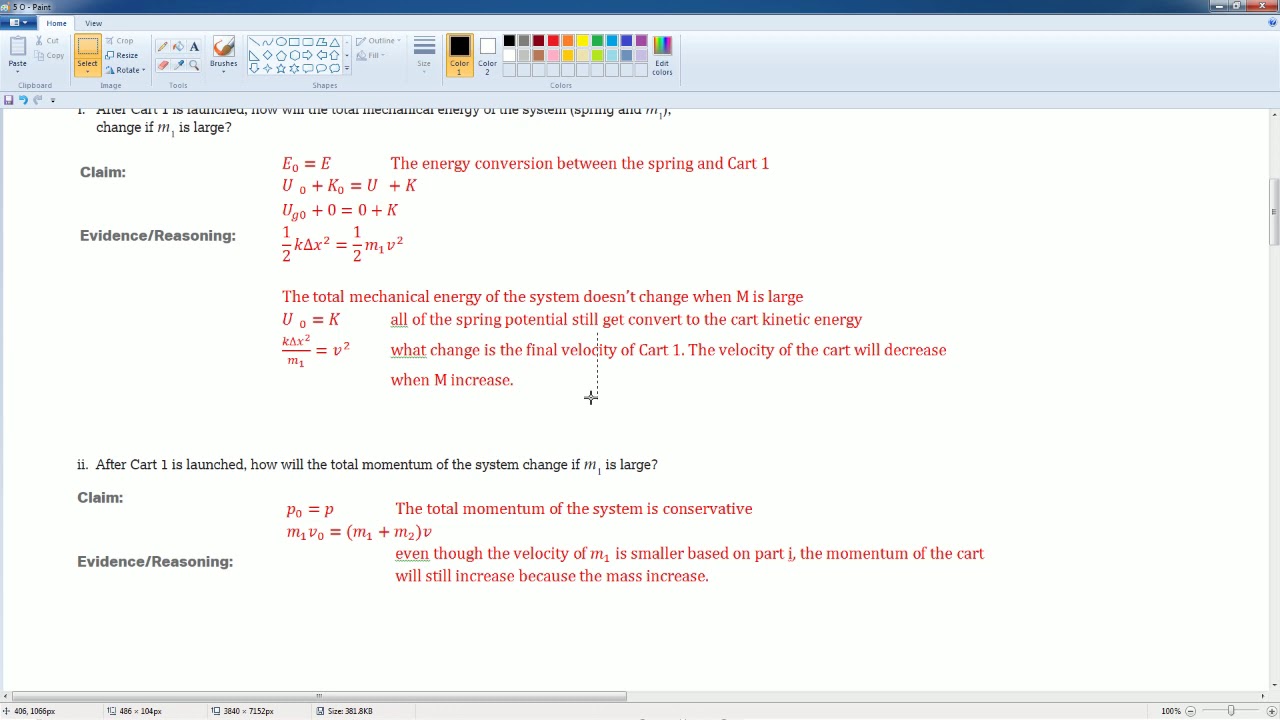
- 🔢 When a dart with a greater mass is launched at the same speed and angle, the block will go higher due to the increased initial momentum and the conservation of momentum principle.
- 📈 The relationship between the collision velocity and the height is quadratic; if the collision velocity doubles, the height increases by a factor of four, and vice versa.
Q & A
What is the main topic of the tutorial?
-The main topic of the tutorial is the 'Five Point G: The Ballistic Pendulum Problem' from the AP Physics workbook.
What principle is applied when a bullet hits a stationary mass and lifts it to a height?
-The principle of conservation of momentum is applied in this scenario. The total momentum before the collision (mv) is equal to the total momentum after the collision (m + M)v', where m is the mass of the bullet, M is the mass of the stationary object, and v' is the velocity after the collision.
How can the conservation of mechanical energy be used in the vertical direction for the ballistic pendulum problem?
-The conservation of mechanical energy in the vertical direction states that the initial kinetic energy (1/2 * (m + M) * v'^2) is equal to the potential energy gained (height * gravitational constant * g). This equation helps to calculate the height the object is lifted after the collision.
What is the equation for the collision velocity in terms of the initial velocity and height?
-The collision velocity (v') can be found using the equation v' = sqrt(2gh), where g is the acceleration due to gravity and h is the height the object is lifted.
How can you find the original velocity of the bullet using the given equations?
-The original velocity (v) can be found by rearranging the equation for collision velocity. By dividing both sides of the equation m * v = (m + M) * v' by m + M, you can solve for v.
What components of velocity are considered in the horizontal direction in this problem?
-In the horizontal direction, the velocity is considered to be constant and is given by v * cos(theta), where v is the initial velocity and theta is the angle of projection.
How does the system's initial momentum affect the final momentum in the horizontal direction?
-According to the conservation of momentum, the initial momentum in the horizontal direction must equal the final momentum. Since the block is initially at rest, its initial momentum is zero. After the collision, the combined system (bullet + block) must have a total horizontal momentum of zero, assuming no external forces act in the horizontal direction.
What happens to the height the block is lifted when the mass of the dart (bullet) is increased?
-When the mass of the dart is increased, the initial momentum in the horizontal direction increases. Since the system conserves momentum, the final momentum also increases, leading to a greater collision velocity. As a result, the height to which the block is lifted increases, because the kinetic energy from the collision is converted into potential energy, which is proportional to the square of the collision velocity (height ∝ v^2).
How does the script demonstrate the relationship between the collision velocity and the height the object is lifted?
-The script shows that the collision velocity squared (v'^2) is directly proportional to the height (h) the object is lifted. This relationship is derived from the conservation of mechanical energy equation, where the initial kinetic energy is equal to the final potential energy. As the collision velocity increases, the height the object is lifted also increases, and vice versa.
What is the significance of including Earth in the system when analyzing the problem?
-Including Earth in the system is important because it accounts for the gravitational potential energy that comes into play when the object is lifted. The gravitational force acting on the object is a key factor in the conservation of mechanical energy principle, which is essential for calculating the height the object is lifted after the collision.
What is the expected outcome if a dart with a greater mass is launched at the same speed and angle as before?
-If a dart with a greater mass is launched at the same speed and angle, the block will be lifted to a greater height. This is because the increased mass of the dart results in a greater initial momentum, leading to a higher collision velocity and, consequently, a greater height due to the conservation of mechanical energy and the relationship between collision velocity and height.
Outlines
📚 Introduction to the Ballistic Pendulum Problem
This paragraph introduces the topic of the video, which is the AP Physics Workbook tutorial on the ballistic pendulum problem. The speaker provides notes for viewers to reference and explains that the problem is a retelling of the textbook's ballistic pendulum problem. The key concept discussed is the conservation of momentum, where the total momentum before the collision (mv) is equal to the total momentum after the collision (m + M)v'. The speaker also explains the conservation of mechanical energy in the vertical direction, stating that the kinetic energy before the collision is equal to the potential energy gained (1/2(m + M)v'^2 = mgh). Two important equations are highlighted: one for the collision velocity (v' = √(2gh)) and another for finding the original velocity (v = mv/(m+M)). The speaker instructs viewers to sketch a horizontal and vertical velocity versus time graph, emphasizing that the horizontal velocity is constant (v*cosθ) and the vertical velocity decreases over time due to gravity (v*sinφ).
🚀 Effect of Dart Mass on Block Height
In this paragraph, the speaker explores the effect of the dart's mass on the height the block is lifted. The speaker explains that the initial momentum of the block is zero because it was at rest, and the conservation of momentum dictates that the final momentum must equal the initial momentum. When a dart with a greater mass is launched at the same speed and angle, the speaker predicts that the block will be lifted higher based on intuition. The speaker then provides a detailed explanation, stating that an increase in the dart's mass leads to an increase in initial momentum (mv = 2p). Since the system is closed and follows conservation of momentum, the final momentum will also increase. The speaker then applies the conservation of energy principle in the vertical direction to show that the initial kinetic energy is converted to final potential energy. The speaker concludes that an increase in collision velocity (v') due to the increased mass of the dart will result in a higher height (h), as shown mathematically by the equation v'^2 = 2gh. The relationship between collision velocity and height is further explained, stating that if the collision velocity doubles, the height quadruples, and vice versa.
Mindmap
Keywords
💡Ballistic Pendulum
💡Conservation of Momentum
💡Collision Velocity
💡Mechanical Energy
💡Projectile Motion
💡Horizontal Component
💡Vertical Component
💡Gravitational Potential
💡Dart and Block System
💡Initial and Final Momentum
💡Velocity versus Time
Highlights
The tutorial covers the Ballistic Pendulum problem from the AP Physics workbook.
Momentum conservation is a key concept in solving the Ballistic Pendulum problem, where the total momentum before the collision equals the total momentum after.
The conservation of mechanical energy in the vertical direction is used to calculate the potential height gained by the system after the collision.
The collision velocity can be found using the equation v = sqrt(2gh), which is crucial for understanding the problem.
The horizontal velocity in the problem is constant because there is no acceleration, and it is given by v cos(theta).
The vertical component of the velocity decreases over time due to the effect of gravity, represented by v sin(phi).
The system to be considered includes the dart, the block, and the Earth, taking into account the gravitational potential.
The initial momentum of the block is zero because it is at rest before the collision.
The final momentum of the system must equal the initial momentum due to the conservation of momentum.
If a dart with greater mass is launched at the same speed and angle, the block will go higher based on the conservation of momentum and energy principles.
An increase in the dart's mass leads to an increase in the initial momentum, which affects the collision velocity and the height gained.
The relationship between the collision velocity and the height is quadratic, as shown by the equation h = (v1^2) / (2g), where an increase in velocity results in a proportional increase in height.
The tutorial provides a detailed explanation of how to apply the principles of conservation of momentum and energy to solve the Ballistic Pendulum problem.
The problem-solving approach involves sketching a horizontal and vertical velocity versus time graph, which helps visualize the motion of the system.
The tutorial emphasizes the importance of understanding the components of velocity in both the horizontal and vertical directions for accurate problem-solving.
The mathematical equations derived from the conservation laws provide a solid foundation for predicting the behavior of the system in the Ballistic Pendulum problem.
The tutorial is a valuable resource for AP Physics students preparing for the exam, offering insights into the application of fundamental physics concepts.
Transcripts
Browse More Related Video
AP Physics Workbook 5.I Momentum Representations
AP Physics Workbook 5.L Inelastic Collisions
AP Physics Workbook 5.O Conservation of Energy and Momentum

Differentiating Between Elastic and Inelastic Collisions | Physics in Motion

AP Physics Workbook 5.J Explosions

2021 AP Physics 1 Free Response #3 (First Administration)
5.0 / 5 (0 votes)
Thanks for rating: