AP Physics Workbook 5.J Explosions

Mr.S ClassRoom
14 Nov 202005:20
EducationalLearning
32 Likes 10 Comments

TLDRThis physics tutorial delves into the concept of momentum conservation, using a scenario where Carlos throws a ball to illustrate the principles. It explains that without external forces, the system's momentum remains constant, leading to a calculation of final velocities for both the ball and a character named Angelica. The tutorial further discusses the transformation of mechanical energy, highlighting an increase when work is done on the ball and a decrease due to energy loss as heat during an inelastic collision. The problem is likened to an explosion, where mechanical energy changes as mass distribution shifts from one to two entities.

Takeaways
  • 📚 The tutorial is based on Unit 5 Momentum from an AP Physics workbook, focusing on the concept of explosion in a hypothetical scenario.
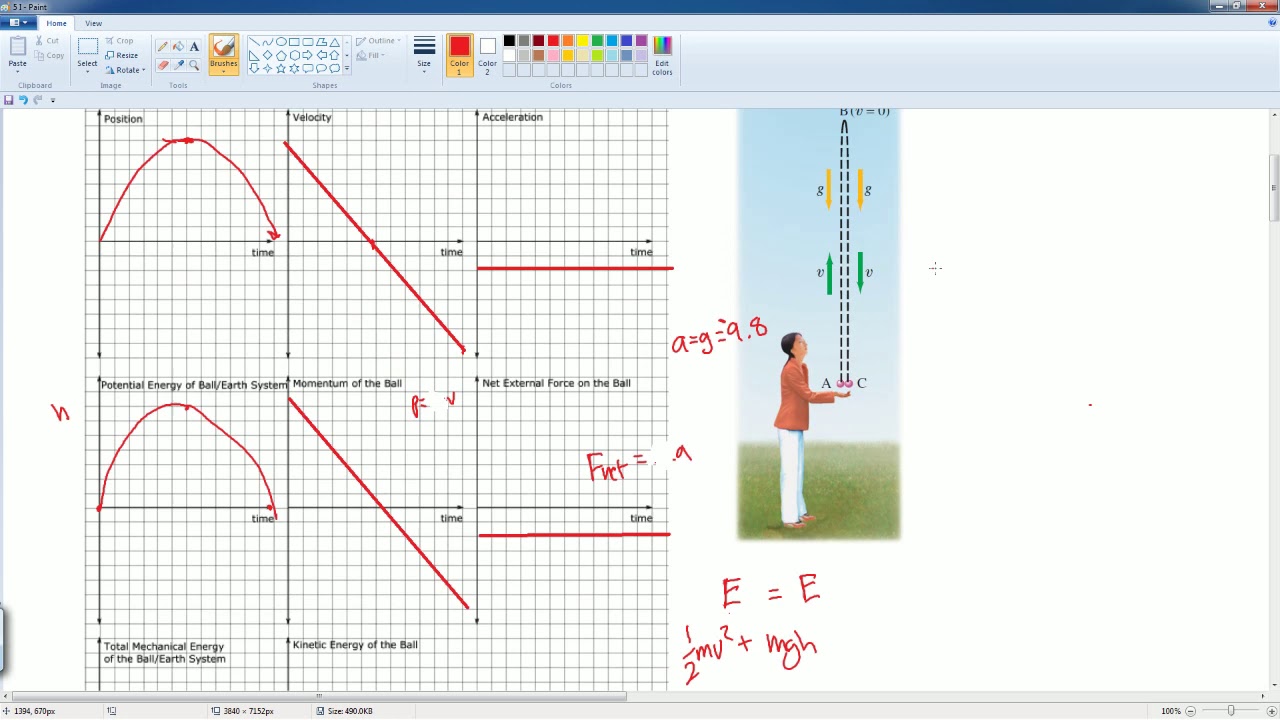
  • 🔄 The problem involves the conservation of momentum, where no external forces result in the system's initial and final momentum being zero.
  • 💡 It is suggested to solve Part B first as it provides the mathematical foundation for Part A.
  • 🏃 The initial and final velocities of Carlos and the ball are used to illustrate the conservation of momentum within the system.
  • 🎾 The ball's interaction with Angelica is also a part of the momentum conservation, with the final momentum being equal to the initial momentum before the collision.
  • 🌟 Newton's third law is discussed, explaining how forces act on both Carlos and the ball when the ball is thrown.
  • 🔄 The shared momentum between the ball and Angelica is a result of the system's conservation of momentum.
  • 📈 The mechanical energy of the system changes when the ball is thrown, indicating an increase due to the work done by Carlos.
  • 🚫 An inelastic collision between the ball and Angelica results in energy loss, primarily in the form of heat.
  • 📊 The ranking of energies (E1 < E3 < E2) is explained, with E1 representing the initial state, E2 the state after the ball is thrown, and E3 after the catch.
  • 💥 The scenario is likened to an explosion where a single mass (the ball) is transformed into two masses (the ball and Angelica).
Q & A

  • What is the main topic of the tutorial?

    -The main topic of the tutorial is the concept of momentum, specifically focusing on an example that mathematically works like an explosion in Unit 5 of the AP Physics Workbook.

  • Why is it recommended to do part B before part A?

    -It is recommended to do part B before part A because part B provides the mathematical foundation needed to understand and answer part A. The conservation of momentum principle discussed in part B is essential for explaining the scenario in part A.

  • What does the conservation of momentum principle state?

    -The conservation of momentum principle states that the total momentum of a system remains constant if no net external forces act on it. This means the initial momentum of the system must equal the final momentum.

  • How does the initial condition of the system (Carlos and the ball) affect the final momentum?

    -Since Carlos and the ball are initially at rest, their initial momentum is zero. According to the conservation of momentum, their final momentum must also be zero, leading to specific velocity relationships between Carlos and the ball after the 'explosion'.

  • What is the role of Newton's third law in this scenario?

    -Newton's third law, which states that for every action, there is an equal and opposite reaction, plays a crucial role in this scenario. When Carlos throws the ball to the right, he experiences a force pushing him to the left, illustrating this law in action.

  • How does the mechanical energy of the system change when the ball is thrown?

    -When the ball is thrown, Carlos does work on the ball, increasing its mechanical energy. This is because the ball now has momentum, and thus the system's total mechanical energy increases compared to the initial state where it was zero.

  • What type of collision is described between Angelica and the ball?

    -The collision between Angelica and the ball is described as inelastic. This means that some energy is lost in the form of heat, resulting in a decrease in the total mechanical energy of the system after the collision.

  • How does the ranking of energies E1, E2, and E3 relate to the conservation of momentum?

    -The ranking E1 < E3 < E2 reflects the changes in mechanical energy of the system due to the 'explosion' and the inelastic collision. E1 represents the initial state with no mechanical energy, E2 represents the increased energy after the ball is thrown, and E3 represents the energy after the inelastic collision where some energy is lost as heat.

  • Why is the scenario described as an 'explosion'?

    -The scenario is described as an 'explosion' because it involves the distribution of momentum from a single mass (Carlos with the ball) to two separate masses (Carlos and Angelica with the ball), which is analogous to how momentum is distributed in an explosion.

  • What is the significance of the denominator in the equation for Angelica's velocity?

    -The denominator in the equation for Angelica's velocity (big m + little m) represents the total mass involved in the system after the 'explosion'. A larger denominator results in a smaller velocity for Angelica because the momentum is shared between her and the ball.

  • How does the tutorial emphasize the importance of understanding momentum conservation?

    -The tutorial emphasizes the importance of understanding momentum conservation by using it as the foundational principle to explain the scenarios in parts A, B, and C. It shows how the conservation of momentum dictates the velocities and mechanical energy changes in the system.

Outlines
00:00
📚 Momentum Conservation in Physics - Problem Analysis

This paragraph introduces a physics problem from a workbook, focusing on the concept of momentum within the context of an explosion analogy. The problem involves two students, Carlos and the ball, and later includes another student, Angelica. The key concept discussed is the conservation of momentum in a system with no net external forces. The explanation begins with a recommendation to solve part B before part A, as it provides the mathematical foundation for the reasoning required in part A. The paragraph delves into the mathematical approach to solving the problem, emphasizing the importance of understanding the conservation of momentum and how it applies to the scenario where Carlos throws the ball. The explanation also touches on the forces experienced by the characters and the distribution of momentum between them. Newton's third law is mentioned to explain the force Carlos experiences when throwing the ball. The paragraph concludes with a discussion on the distribution of momentum between the ball and Angelica after a collision, highlighting the conservation of momentum as a key factor in determining their final velocities.

05:03
💥 Exploring the 'Explosive' Scenario in Physics

This paragraph concludes the video script by likening the physics problem to an explosion, where a single mass (the ball) is separated into two masses (the ball and Angelica). The analogy is used to illustrate the concept of momentum distribution in a simple and relatable manner. The paragraph reinforces the idea that the conservation of momentum is a fundamental principle in physics, applicable even in scenarios that may seem complex or abstract at first glance. The use of the 'explosion' analogy helps to clarify the underlying physics concepts, making them more accessible and easier to understand for the viewer.

Mindmap
Keywords
💡Momentum
Momentum is a fundamental concept in physics that represents the quantity of motion of an object. It is the product of an object's mass and velocity. In the context of the video, momentum is conserved in a closed system, meaning the total momentum before an event (like an explosion or a collision) is equal to the total momentum after the event. This principle is crucial in solving problems related to the motion of objects, such as the ones discussed in the video involving Carlos, the ball, and Angelica.
💡Conservation of Momentum
The law of conservation of momentum states that the total momentum of a closed system remains constant if no external forces act on it. This principle is a key aspect of the video's explanation, as it is used to determine the final velocities of the ball and Angelica after the collision. The script illustrates this by explaining that the initial momentum of the system (Carlos and the ball) must equal the final momentum (the combined momentum of the ball and Angelica).
💡Explosive Scenario
An explosive scenario, in the context of this video, refers to a situation where an object (like a ball) is separated into multiple parts (the ball and the person catching it), causing a distribution of momentum among these parts. This concept is used to explain the problem as if it were an explosion, even though there isn't an actual explosion occurring. The term 'explosion' in this case is used metaphorically to describe the transfer and redistribution of momentum.
💡Newton's Third Law
Newton's Third Law states that for every action, there is an equal and opposite reaction. In the video, this law is illustrated when Carlos throws the ball; he experiences a force pushing him to the left, while the ball is propelled to the right. This law is essential in understanding how the momentum is transferred from Carlos to the ball and later shared between the ball and Angelica.
💡Inelastic Collision
An inelastic collision is a type of collision where the colliding objects stick together after the impact, and some kinetic energy is converted into other forms of energy, like heat or sound, resulting in a loss of mechanical energy. In the video, the collision between the ball and Angelica is described as inelastic, meaning that after the collision, there is less mechanical energy in the system compared to before the collision.
💡Mechanical Energy
Mechanical energy is the sum of potential energy and kinetic energy in a system. It is a key concept in the video as it helps to understand the changes in energy before and after the ball is thrown and when the collision occurs. The video explains that there is no mechanical energy before the ball is thrown (E1), an increase in mechanical energy after the ball is thrown (E2), and a decrease after the inelastic collision (E3).
💡Velocity
Velocity is a vector quantity that describes the rate of change of an object's position with respect to time, and it has both magnitude (speed) and direction. In the video, the concept of velocity is essential for calculating the momentum of the objects and determining their final velocities after the interactions. The script discusses the final velocities of Carlos and Angelica as part of the momentum conservation equations.
💡Mass
Mass is a measure of the amount of matter in an object, and it is a fundamental property that affects the object's inertia and the gravitational force it experiences. In the video, the mass of the ball and the mass of Angelica are important factors in the conservation of momentum equations and the calculation of their final velocities after the collision.
💡Work
In physics, work is done when a force causes an object to move in the direction of the force. It is calculated as the product of the force applied and the distance moved by the object in the direction of the force. In the video, Carlos does work on the ball when he throws it, which increases the ball's momentum and, consequently, its mechanical energy.
💡Force
Force is any action that causes an object to accelerate or change its motion. In the context of the video, force is the interaction between Carlos and the ball, as well as between the ball and Angelica during the collision. Forces are responsible for the changes in momentum and velocities of the objects involved.
💡Kinetic Energy
Kinetic energy is the energy that an object possesses due to its motion. It is directly proportional to the mass of the object and the square of its velocity. In the video, the kinetic energy of the system changes as the ball is thrown and when the collision occurs, affecting the total mechanical energy.
💡Potential Energy
Potential energy is the stored energy an object has due to its position or state. In the context of the video, although not explicitly mentioned, it can be inferred that there is no potential energy involved before the ball is thrown since the system has no mechanical energy (E1). Potential energy could come into play if the ball was at a height before being thrown, but in this scenario, it is not a factor.
Highlights

Exploration of momentum conservation in an ap Physics workbook context.

The problem simulates an explosion scenario without an actual explosion, focusing on the mathematical aspect of momentum transfer.

Recommendation to solve part B before part A to understand the underlying mathematical principles.

Explanation of the conservation of momentum with the system comprising Carlos and the ball, and the absence of net external forces.

Initial and final momentum of Carlos and the ball being zero, demonstrating the conservation of momentum.

Derivation of the final velocity equation for Carlos using the conservation of momentum principle.

Introduction of the second system involving the ball and Angelica, with a focus on the conservation of momentum during the collision.

Calculation of Angelica's velocity after the collision, emphasizing the non-zero momentum due to the ball's mass.

Connection between the initial momentum of the system (Carlos, ball, and Angelica) and the final momentum after the throw.

Explanation of the force experienced by Carlos due to Newton's third law when he throws the ball.

Discussion on the distribution of momentum between the ball and Angelica, and its effect on their velocities.

Comparison of final velocities of Carlos and Angelica, with Angelica having a smaller speed due to the combined mass.

Explanation of the energy rankings (E1, E2, E3) in the context of mechanical energy, work done, and energy loss due to heat.

E1 represents the system with no mechanical energy before the ball was thrown.

E2 signifies the increase in mechanical energy after Carlos throws the ball, indicating work done on the ball.

E3 corresponds to the energy after the inelastic collision between Angelica and the ball, where some energy is lost as heat.

E1 is the smallest as it represents the initial state with zero mechanical energy.

The problem is likened to an explosion because the momentum of one mass is divided between two masses after separation.

Transcripts

Browse More Related Video

AP Physics Workbook 5.I Momentum Representations

College Physics 1: Lecture 27 - Conservation of Momentum

AP PHYSICS 1: Unit 5 FRQ 2 (AP Physics Classroom)

Differentiating Between Elastic and Inelastic Collisions | Physics in Motion

AP Physics 1 Momentum Review

AP Physics Workbook 4.B Choosing Systems

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
PhysicsConceptsMomentumConservationEnergyTransformationAPPhysicsWorkbookTutorialMechanicalEnergyInelasticCollisionProblemSolvingEducationalContentScienceEducation