07 - What is Instantaneous Velocity?, Part 1 (Instantaneous Velocity Formula & Definition)
TLDRIn this lesson, the concept of instantaneous velocity is explored, contrasting it with average velocity. The video explains that while average velocity is the total distance divided by total time, instantaneous velocity refers to the speed of an object at a specific moment in time. Through the use of motion graphs and the concept of a tangent line, the lesson illustrates how the slope of the tangent line at a point on a position-time graph represents the instantaneous velocity at that point. The lesson also touches on the concept of limits in calculus as a means to find this instantaneous velocity precisely.
Takeaways
- 📚 The concept of instantaneous velocity is introduced as a way to understand the velocity of an object at a specific moment in time, as opposed to average velocity which considers the overall motion over a period.
- 🔄 The lesson begins with a review of average velocity, defined as distance divided by time (Δx/Δt), and its representation on a graph as a straight line indicating constant speed.
- 📈 The importance of understanding the slope of a line in the context of position-time graphs is emphasized, where the slope represents the average velocity of the object.
- 💫 The introduction of calculus is motivated by the need to analyze more complex motions where the position graph is not a straight line, but a curve reflecting changes in velocity.
- 🌐 The concept of a tangent line is used to approximate the instantaneous velocity at a point on a curve by drawing a line that just touches the curve at that specific point.
- 🎯 To estimate instantaneous velocity, the process of finding the average velocity between two points on the curve and narrowing the interval between those points is discussed.
- 🔢 The mathematical concept of 'limit' is introduced as the approach to finding the instantaneous velocity, which involves letting the time interval (Δt) approach zero while calculating the corresponding change in position (Δx).
- 🚀 The instantaneous velocity at a point is the limit of the average velocity as the time interval becomes infinitesimally small.
- 🛤️ The distinction between positive and negative slopes is clarified, with positive slopes indicating motion in the positive x-direction and negative slopes indicating motion in the negative x-direction.
- 📊 The graphical representation of motion is a key tool in understanding both average and instantaneous velocities, with the position-time graph providing a visual representation of an object's motion and velocity.
- 🌟 The lesson concludes by reinforcing the idea that the slope of the tangent line at any point on a position-time graph represents the instantaneous velocity of the object at that specific moment in time.
Q & A
What is the main concept being discussed in the lesson?
-The main concept discussed in the lesson is instantaneous velocity, which is the velocity of an object at a specific moment in time, as opposed to average velocity which is calculated over a period of time.
How is average velocity defined and calculated?
-Average velocity is defined as the total distance traveled divided by the total time taken. It is calculated using the formula V_avg = Δx / Δt, where Δx is the change in position and Δt is the change in time.
What is the significance of the slope in a position-time graph?
-The slope in a position-time graph represents the average velocity of the object. A positive slope indicates motion in the positive x-direction, while a negative slope indicates motion in the negative x-direction.
How does a straight line in a position-time graph relate to the object's motion?
-A straight line in a position-time graph indicates that the object is moving at a constant velocity, meaning its speed does not change over the time interval represented by the line.
What is instantaneous velocity and how does it differ from average velocity?
-Instantaneous velocity is the velocity of an object at a specific instant or point in time. It differs from average velocity, which is calculated over a period of time and does not provide information about the object's speed at any particular moment within that period.
How can we estimate instantaneous velocity from a position-time graph?
-We can estimate instantaneous velocity by drawing a tangent line to the position-time graph at the point of interest and calculating the slope of that tangent line. The slope of the tangent line at a point represents the instantaneous velocity at that point.
What is the mathematical concept used to find the exact instantaneous velocity?
-The mathematical concept used to find the exact instantaneous velocity is the limit. It involves taking the limit as the time interval approaches zero, which gives the instantaneous velocity at a specific point.
Why is calculus introduced in the context of instantaneous velocity?
-Calculus is introduced because it provides the mathematical tools necessary to deal with rates of change at specific moments in time, which is the essence of instantaneous velocity. It allows us to calculate the exact slope of the tangent line at any point on the position-time graph.
How does the shape of the position-time graph relate to the object's acceleration?
-The shape of the position-time graph can indicate whether the object is accelerating or decelerating. If the graph is a curved line, it suggests that the object's velocity is changing, which means it is accelerating or decelerating. A straight line indicates constant velocity and no acceleration.
What is the relationship between the slope of the tangent line and the object's velocity at a point?
-The slope of the tangent line at a point on the position-time graph is equal to the instantaneous velocity of the object at that point. It provides a precise measure of the object's speed at that specific moment in time.
How does the concept of a limit help in understanding motion?
-The concept of a limit allows us to understand the behavior of a function (such as velocity) as it approaches a particular point. In the context of motion, it helps us determine the instantaneous velocity, which is the speed of an object at a specific instant, by considering what the average velocity over an increasingly small time interval approaches.
Outlines
📚 Introduction to Instantaneous Velocity and Review of Average Velocity
This paragraph introduces the concept of instantaneous velocity, following a brief review of average velocity. It sets the stage for the lesson by mentioning the importance of understanding velocity at a specific instant and touches on the role of calculus in physics. The instructor reassures students that calculus, despite its reputation, is not intimidating and will be explained in a way that is accessible even to a kindergartener. The historical context of calculus as a tool to explain nature is also highlighted.
📈 Understanding Position-Time Graphs and the Concept of Slope
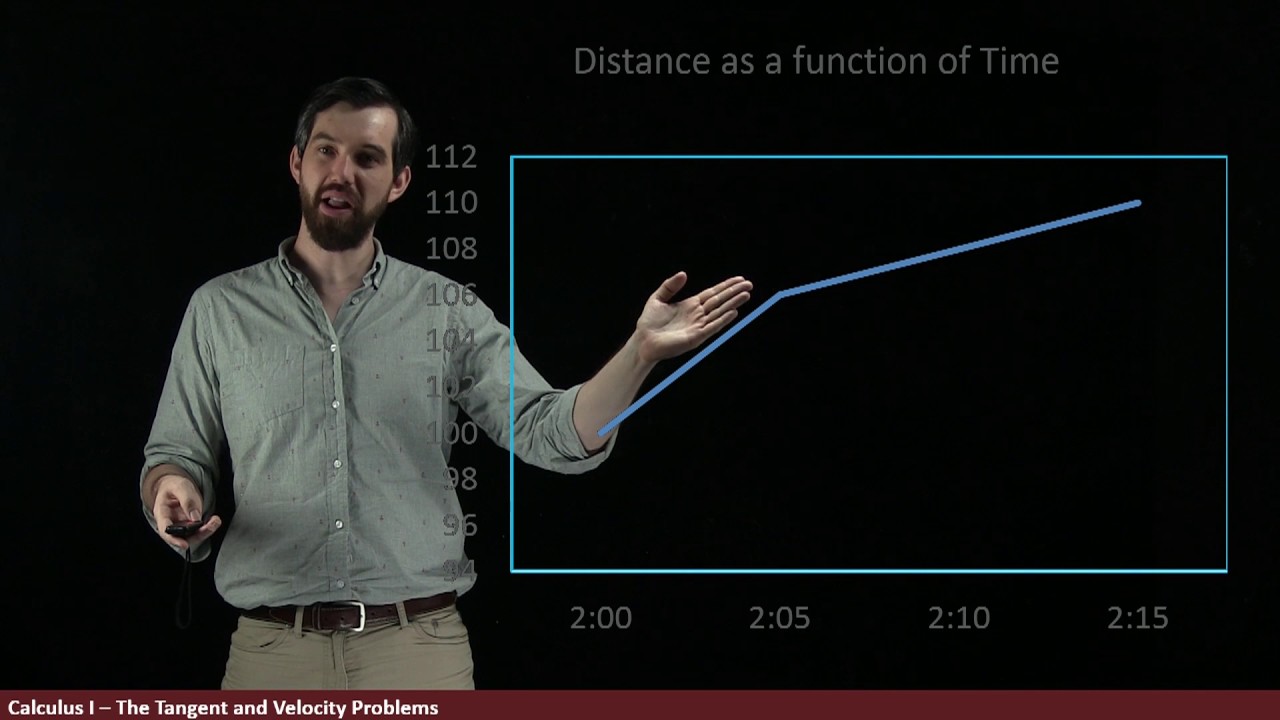
The paragraph delves into the details of position-time graphs, explaining how the slope of a straight line on such a graph represents constant velocity. It illustrates this with an example of a person walking at a consistent speed from point A to point B. The concept of slope as the rise over run is introduced, and it is related to the average velocity, which is calculated as the change in position (ΔX) divided by the change in time (ΔT). The paragraph emphasizes that the slope remains constant for a straight line, indicating a constant velocity throughout the motion.
🚶♂️ Analyzing Curved Position-Time Graphs and Instantaneous Velocity
This paragraph discusses the implications of a curved position-time graph, suggesting that a changing slope indicates a change in velocity. The instructor uses a hypothetical scenario where the velocity varies over time, with the individual covering more distance with each passing second, indicating acceleration. The concept of instantaneous velocity is further explored by discussing the tangent line to the curve at a specific point, which has a slope representing the instantaneous velocity at that point.
📊 Estimating Instantaneous Velocity from a Position-Time Graph
The paragraph explains how to estimate instantaneous velocity by drawing a line segment between two points on a curved position-time graph and calculating its slope. The closer the second point (B) is to the point of interest (A), the better the approximation of the instantaneous velocity. The process of moving point B closer to point A to refine the estimate is described, culminating in the idea of taking the limit as the time interval (ΔT) approaches zero to find the precise instantaneous velocity.
🌟 The Limit Process and Calculating Instantaneous Velocity
This paragraph clarifies the process of finding the instantaneous velocity at a point by taking the limit as the time interval approaches zero. It explains that as the time difference becomes infinitesimally small, the average velocity between two points on the curve approaches the instantaneous velocity at a specific point. The concept is tied back to the fundamental ideas in calculus, emphasizing that the instantaneous velocity is the slope of the tangent line to the position-time curve at a given moment.
Mindmap
Keywords
💡Instantaneous Velocity
💡Average Velocity
💡Position-Time Graph
💡Slope
💡Limit
💡Delta X and Delta T
💡Calculus
💡Tangent Line
💡Rise Over Run
💡Positive and Negative Slopes
Highlights
The lesson covers the concept of instantaneous velocity, building upon the understanding of average velocity.
A brief review of average velocity is provided, emphasizing its calculation as distance divided by time.
The introduction of calculus is motivated by the need to understand the velocity of an object at any given instant.
The foundational purpose of calculus is explained as a tool to describe the natural world and motion.
The concept of average velocity is clarified through the use of the Greek letter Delta (Δ) to represent change.
A motion graph is introduced to visually demonstrate the concept of constant velocity with a straight line.
The significance of the slope of a line in the context of position-time graphs is discussed as it relates to velocity.
The difference between average and instantaneous velocity is highlighted, with the latter providing a more detailed view of motion.
The concept of a tangent line and its slope at a specific point on a curve is introduced as a method to approximate instantaneous velocity.
The process of taking a limit as time approaches zero to find the instantaneous velocity is outlined.
The importance of understanding both positive and negative slopes in the context of velocity is discussed.
A graphical estimation method for instantaneous velocity is demonstrated using a line segment between two points.
The concept of a limit in calculus is applied to find the exact instantaneous velocity at a point on a curve.
The lesson emphasizes the practical application of calculus in physics, particularly in understanding motion.
The relationship between the slope of a position-time graph and the velocity of an object is established as a key takeaway.
The lesson concludes by reinforcing the idea that instantaneous velocity can be found by calculating the limit of the slope of a tangent line on a position-time graph.
Transcripts
Browse More Related Video

Intro to Derivatives, Limits & Tangent Lines in Calculus | Step-by-Step

Understanding Differentiation Part 2: Rates of Change
The Velocity Problem | Part II: Graphically

Average/Instantaneous Rates of Changes

AP Daily: AP Calculus BC (1.1)
13 - Instantaneous Acceleration Explained (Average Vs. Instantaneous Acceleration)
5.0 / 5 (0 votes)
Thanks for rating: