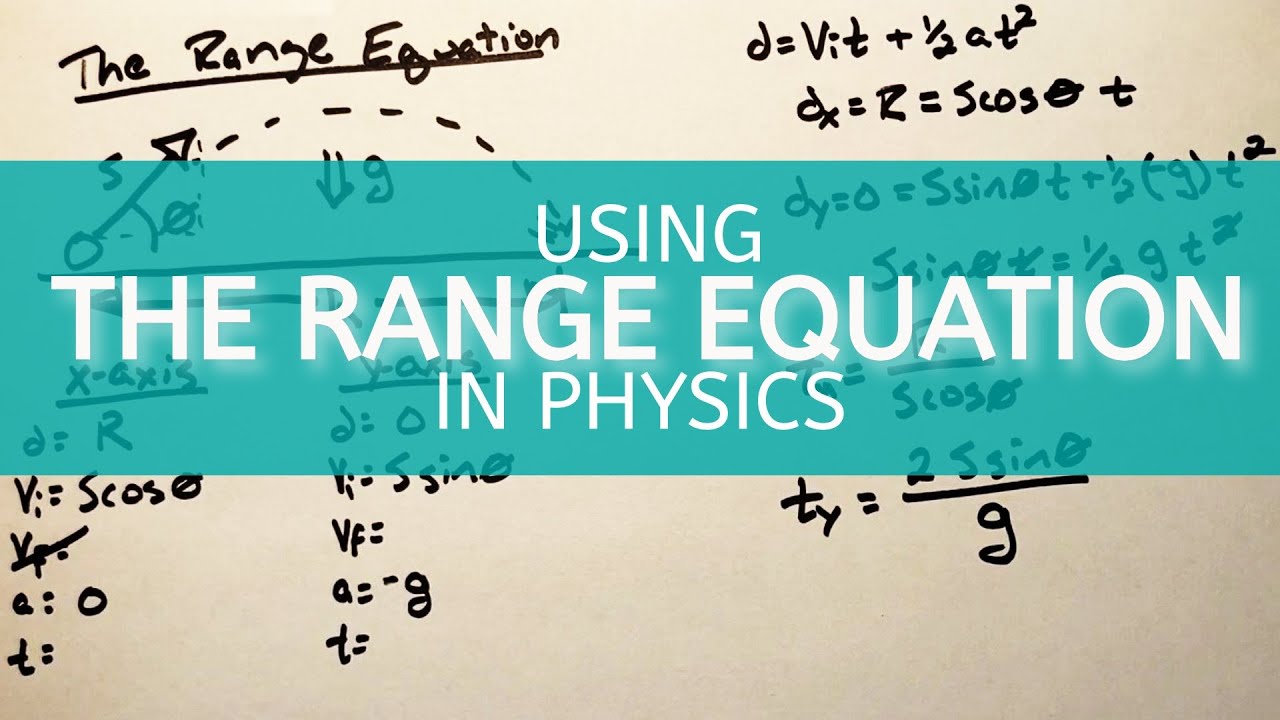Projectile Motion - Maximum Range Angle - Physics & Calculus
TLDRThe video script explains the concept of projectile motion and how to calculate the angle that yields the maximum range for a ball launched at ground level. It introduces the range formula and uses calculus to derive the optimal angle, confirming the common intuition that 45 degrees is the angle for maximum horizontal distance. The explanation is clear, engaging, and informative, providing viewers with a solid understanding of the underlying principles and the mathematical process involved.
Takeaways
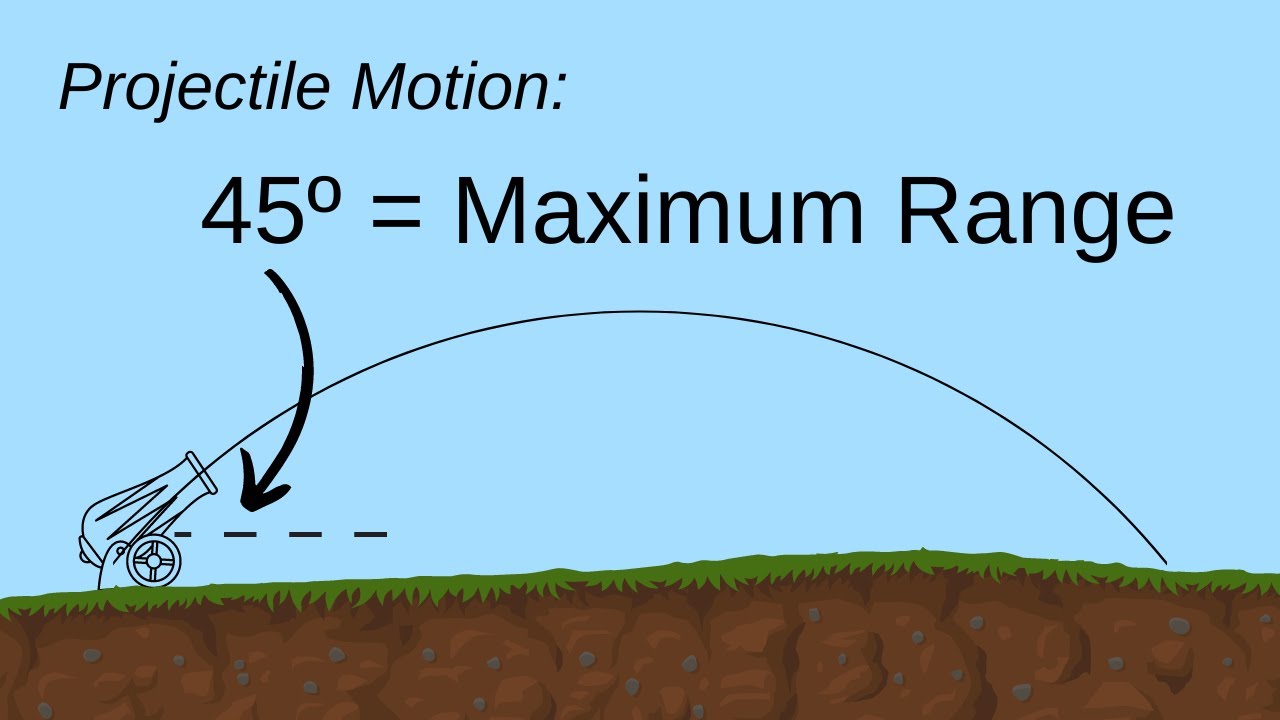
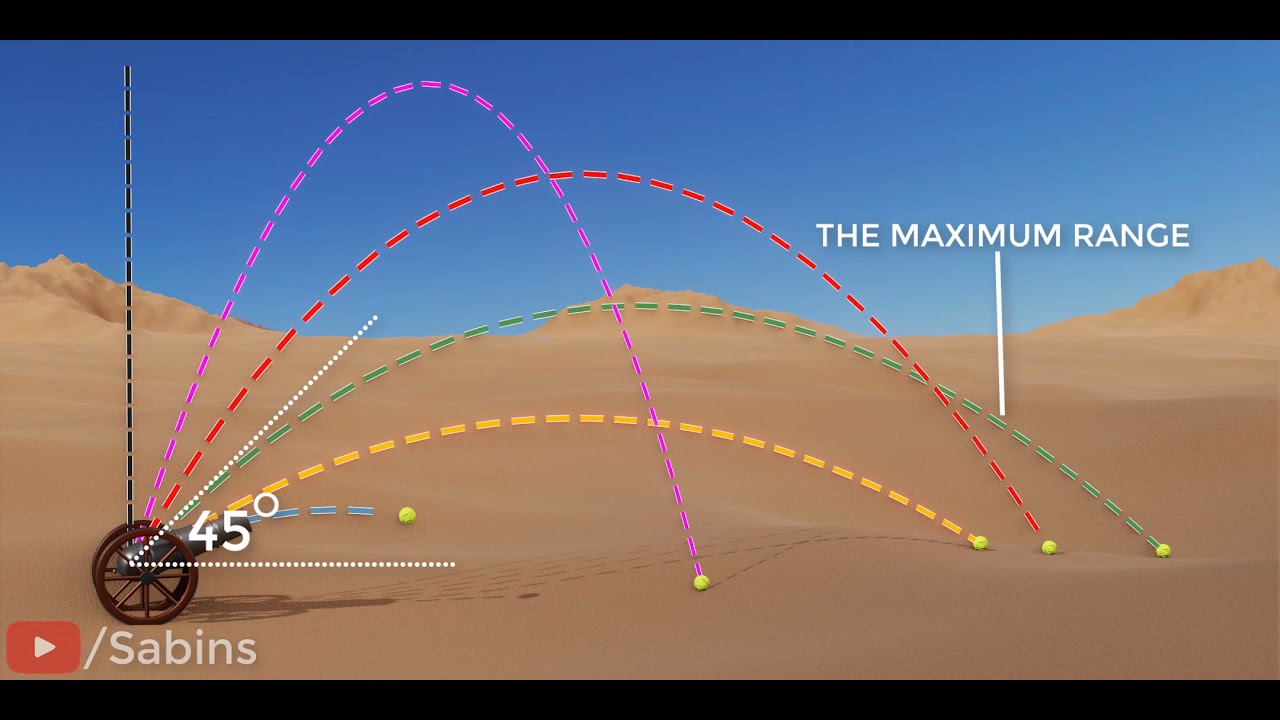
- 🚀 The maximum range of a projectile motion occurs at an angle of 45 degrees.
- 📈 The range (R) is calculated using the formula R = V^2 * sin(2Θ) / G, where V is the initial velocity, Θ is the launch angle, and G is the gravitational acceleration.
- 🧮 To find the angle for maximum range, calculus is used to determine the angle where the derivative of the range with respect to Θ equals zero.
- 🔄 At a local maximum or minimum, the slope of the curve (or tangent) is horizontal, meaning the derivative is zero.
- 📌 The derivative of the range with respect to Θ involves differentiating V^2 * sin(2Θ) / G with respect to Θ, treating V and G as constants.
- 📐 The derivative of sin(2Θ) using the chain rule results in 2 * cos(2Θ), with 2 being the derivative of the angle's coefficient.
- 🎯 Setting the derivative equal to zero and solving for Θ yields an equation where cos(2Θ) = 0.
- 🌟 The arc cosine of zero is 90 degrees, indicating that 2Θ = 90, thus Θ = 45 degrees.
- 🔄 The process involves canceling out constants and coefficients to isolate the variable Θ.
- 🏹 This method applies to level projectile motion problems, where the launch is from ground level and not from an elevated position.
- 📚 Understanding this process allows for the application of calculus to solve real-world physics problems.
Q & A
What is the primary focus of the transcript?
-The primary focus of the transcript is to explain how to calculate the angle at which a projectile launched from ground level will have the maximum range using calculus.
What is the formula for the range of a projectile?
-The formula for the range of a projectile is given by R = V^2 * sin(2Θ) / G, where R is the range, V is the velocity, Θ is the angle of launch, and G is the gravitational acceleration.
What is the significance of the angle in the context of projectile motion?
-The angle in projectile motion determines the trajectory of the object. The angle at which the maximum range is achieved is important for optimizing the horizontal distance the object will travel.
Why is the angle of 45 degrees often associated with maximum range in projectile motion?
-The angle of 45 degrees is associated with maximum range because it allows the sine function to achieve its maximum value of 1, which in turn maximizes the range according to the given formula.
How does calculus help in finding the angle for maximum range?
-Calculus is used to find the angle for maximum range by taking the derivative of the range function with respect to the angle, setting it to zero, and solving for the angle. This process identifies the angle where the slope of the range curve is horizontal, indicating a maximum or minimum.
What is the process of differentiating the range with respect to angle Theta?
-The process involves taking the derivative of the range function R = V^2 * sin(2Θ) / G with respect to Theta, setting the derivative equal to zero, and solving for Theta to find the angle that maximizes the range.
What is the role of the velocity and gravitational acceleration in the differentiation process?
-During the differentiation process with respect to Theta, the velocity (V) and gravitational acceleration (G) are treated as constants because they do not change with respect to Theta.
How does the derivative of sine function affect the calculation?
-The derivative of the sine function with respect to Theta is cosine function. When differentiating the range with respect to Theta, the sine function's derivative is used to find the critical points where the range might be maximized or minimized.
What is the result of setting the derivative of the range function to zero?
-Setting the derivative of the range function to zero yields an equation where the cosine of 2Θ is equal to zero. This leads to the conclusion that the maximum range occurs when 2Θ is 90 degrees, making Theta equal to 45 degrees.
How does the arc cosine function help in finding Theta?
-After setting the derivative equal to zero and simplifying, the arc cosine function is applied to isolate Theta. It is used to find the angle whose cosine is zero, which corresponds to an angle of 90 degrees when doubled (2Θ). Dividing by two gives the value of Theta as 45 degrees.
What is the practical application of this calculation?
-The practical application of this calculation is in determining the optimal angle for launching projectiles to achieve the greatest horizontal distance in various scenarios such as sports, military operations, or physics experiments.
Outlines
🚀 Calculating the Optimal Launch Angle for Maximum Range
This paragraph discusses the concept of achieving maximum horizontal range for a projectile launched at ground level. It introduces the problem by describing the trajectory of a ball launched at an angle Theta and poses the question of determining the angle that yields the maximum range. The speaker clarifies that while many may intuitively know the answer to be 45 degrees, the video aims to derive this angle using calculus. The range formula provided is Range = V^2 * sin(2Theta) / G, where V is the initial velocity, G is the gravitational acceleration, and Theta is the launch angle. The paragraph then delves into the process of using calculus to find the angle that maximizes the range, explaining the concept of local maximum and the role of derivatives in identifying such points. By differentiating the range with respect to Theta and setting the derivative equal to zero, the speaker solves for Theta and confirms that the angle yielding maximum range is indeed 45 degrees for a level projectile motion.
🎯 Confirming the 45-Degree Angle for Maximum Range
In this paragraph, the speaker reinforces the conclusion from the previous section, stating that for a projectile launched from ground level with a trajectory as described, the maximum range is achieved at an angle of 45 degrees. The paragraph serves as a recap and confirmation of the process used to calculate this optimal angle using calculus. It emphasizes the practical application of the method and the understanding gained from the mathematical derivation, providing viewers with a clear understanding of how to apply calculus to real-world physics problems, specifically in the context of projectile motion and determining the launch angle for maximum distance.
Mindmap
Keywords
💡Projectile Motion
💡Trajectory
💡Range
💡Angle Theta
💡Calculus
💡Derivative
💡Slope
💡Local Maximum
💡Chain Rule
💡Arc Cosine
💡Optimal Angle
💡Velocity
Highlights
The discussion is about determining the angle for maximum range in projectile motion.
The angle intuitively known to provide maximum range is 45 degrees.
The method used to calculate the angle is through the use of calculus.
The formula for range in terms of velocity (V), angle (Theta), and gravitational acceleration (G) is given as Range = V^2 * sin(2Theta) / G.
The process involves finding the derivative of the range with respect to Theta and setting it to zero to find the maximum.
The derivative of the range function involves the derivative of sine and the chain rule.
The derivative is set to zero, leading to the equation 0 = cos(2Theta) after simplification.
The arc cosine of zero is 90 degrees, indicating that 2Theta equals 90 degrees at the maximum range condition.
Theta is half of 90 degrees, which confirms the angle of 45 degrees for maximum range.
The maximum range is achieved when the projectile is launched from ground level in a level trajectory.
The process demonstrated is a practical application of calculus in physics.
The video aims to provide a deeper understanding beyond intuition by showing the calculation.
The angle of 45 degrees is applicable for a horizontal launch, not from an elevated position.
The explanation covers the basics of finding local maximum or minimum using derivatives.
The use of trigonometric function derivatives and the chain rule is crucial in the calculation.
The final result confirms the widely known fact in projectile motion problems.
The method can be applied to other similar problems involving optimization.
The transcript provides a comprehensive walkthrough of the mathematical process.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: