Position, Velocity, Acceleration using Derivatives

patrickJMT
28 Feb 201108:46
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the relationship between position, velocity, and acceleration, explaining how derivatives and integrals are used to transition between these physical quantities. The core concept is that the derivative of position with respect to time gives velocity, and the derivative of velocity gives acceleration. The script illustrates this with a mechanical problem, showing how to calculate velocity and acceleration at a specific time using the given position equation. The explanation emphasizes the practical application of calculus in understanding motion, highlighting the significance of instantaneous rate of change in physics.

Takeaways
  • 📌 The relationship between position, velocity, and acceleration is fundamental in understanding motion.
  • 🔄 The derivative of position with respect to time gives the velocity.
  • 📈 The derivative of velocity with respect to time yields the acceleration.
  • 🅰️ Position is often abbreviated as s(T), where T represents time.
  • 🚀 Velocity has a sign indicating direction (positive for right or forward, negative for left or backward).
  • 🛤️ Speed is the absolute value of velocity and is always positive.
  • 📶 To find the velocity at a specific time, substitute that time into the velocity equation derived from the position function.
  • 🏎️ Acceleration is found by taking the derivative of the velocity function, which is the second derivative of the position function.
  • 📌 An example motion equation is s = 5T^3 + 3T + 8, where T is in seconds and s in meters.
  • 🕒 To calculate the velocity after two seconds, derive the position function and substitute T = 2 into the derivative.
  • 🌪️ The acceleration after two seconds can be found by taking the derivative of the velocity function and substituting T = 2.
Q & A

  • What is the relationship between position, velocity, and acceleration?

    -The derivative of position with respect to time gives you velocity, and the derivative of velocity with respect to time gives you acceleration.

  • How is velocity represented in terms of position?

    -Velocity is represented by taking the first derivative of the position function with respect to time.

  • What does the sign of velocity indicate?

    -The sign of velocity indicates the direction of motion. Positive velocity indicates movement in the positive direction, while negative velocity indicates movement in the opposite direction.

  • How can you find the instantaneous rate of change of velocity?

    -You can find the instantaneous rate of change of velocity by taking the derivative of the velocity function, which gives you the acceleration.

  • What is the equation for the displacement of a particle given in the example?

    -The equation for the displacement of a particle is s = 5T^3 + 3T + 8, where T is measured in seconds.

  • What is the velocity of the particle after 2 seconds according to the given equation?

    -The velocity after 2 seconds is 15(2)^2 + 3 = 60 + 3 = 63 meters per second.

  • How can you find out when the velocity equals a specific value, such as 100 meters per second?

    -You would set the velocity equation equal to the desired velocity value (100 in this case) and solve for the time variable T.

  • What is the acceleration of the particle after 2 seconds according to the given equation?

    -The acceleration after 2 seconds is 15(2)^2 + 3 = 30(2) + 3 = 60 meters per second squared.

  • Why is understanding the relationship between position, velocity, and acceleration important?

    -Understanding these relationships is crucial in kinematics and dynamics as they provide insights into the motion of an object, including its speed, direction, and how these change over time.

  • What does the derivative quantify?

    -The derivative quantifies the instantaneous rate of change of a function with respect to its variable, which in the context of motion, can represent changes in position, velocity, or acceleration.

  • How does the concept of derivatives relate to real-world physical situations like driving a car?

    -The derivative in the context of driving relates to the rate at which distance changes, which is the speed of the car. The rate of change of speed over time gives acceleration, providing insights into how quickly the car's speed is changing.

  • What is the antiderivative of acceleration with respect to time?

    -The antiderivative of acceleration with respect to time gives you the velocity function, and taking the antiderivative of the velocity function gives you the position function.

Outlines
00:00
📐 Understanding Position, Velocity, and Acceleration

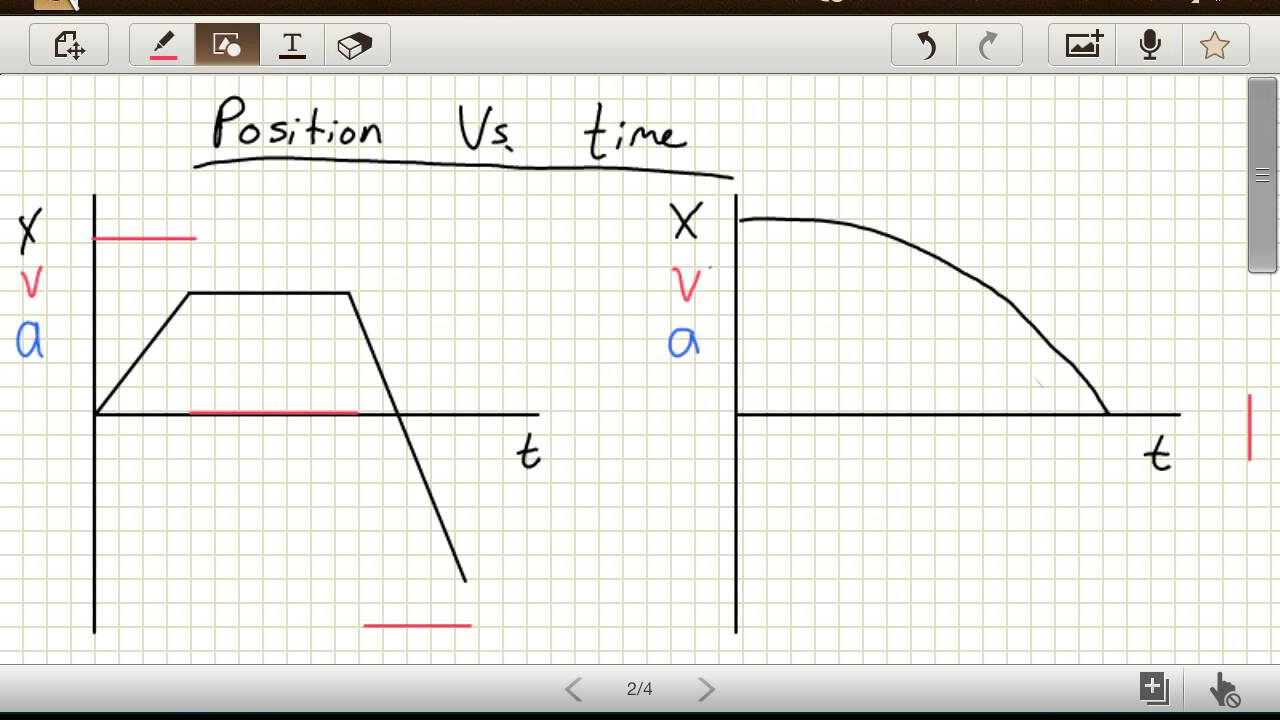
This paragraph introduces the fundamental concepts of position, velocity, and acceleration, and their interrelationships. It explains that the derivative of a position function represents velocity, and further differentiating velocity yields acceleration. The explanation includes the use of mathematical notation (e.g., s(t) for position) and emphasizes the importance of the sign in velocity to indicate direction. The paragraph also touches on the concept of speed, which is the absolute value of velocity, and sets up a context for a mechanical problem involving calculating velocity and acceleration from a given position function.

05:01
🔢 Calculating Velocity and Acceleration from Position

The second paragraph delves into the practical application of the concepts introduced earlier. It presents a specific problem where the displacement of a particle is given by the equation s = 5t^3 + 3t + 8, and the task is to find the velocity and acceleration after two seconds. The paragraph outlines the process of taking derivatives of the position function to obtain the velocity function and then another derivative to find the acceleration. It provides a step-by-step calculation, including plugging in the value of time (t=2s) to get the numerical results for velocity (63 m/s) and acceleration (60 m/s^2). The paragraph also briefly discusses how to find when the velocity reaches a certain value, such as 100 m/s, by solving the velocity equation for time.

Mindmap
Keywords
💡position
In the context of the video, 'position' refers to the location of an object in space at a given time, typically represented by a function s(T) where T is time. It is a fundamental concept in kinematics, the study of motion, and is used to describe the path taken by an object. For example, the video discusses a particle moving in a straight line with its position given by the equation s = 5T^3 + 3T + 8, where T is measured in seconds.
💡velocity
Velocity is defined as the rate of change of position with respect to time, indicating how fast an object is moving and in which direction. It is derived from the position function by taking its first derivative. In the video, the sign of the velocity indicates the direction of motion; positive velocity means moving to the right or away, while negative velocity indicates moving to the left or towards. Instantaneous velocity can be used to describe the speed of an object at a specific moment in time.
💡acceleration
Acceleration is the rate of change of velocity with respect to time, which describes how quickly the velocity of an object is changing. It is derived by taking the second derivative of the position function or the first derivative of the velocity function. Acceleration provides insight into the dynamics of an object's motion, such as whether it is speeding up, slowing down, or changing direction. The video explains that the acceleration function a(T) = 30T, obtained by differentiating the velocity function, gives the acceleration in meters per second squared at any time T.
💡derivative
The derivative is a fundamental concept in calculus that represents the rate of change or the slope of a function at a particular point. In the context of the video, derivatives are used to relate position, velocity, and acceleration. The first derivative of a position function gives the velocity, and the second derivative gives the acceleration. Derivatives are essential for understanding the behavior of functions and their applications in physics and engineering.
💡displacement
Displacement refers to the change in position of an object, typically measured from a reference point such as the starting point. In the video, displacement is used to describe the straight-line motion of a particle, with the position function s(T) representing the displacement in meters at any given time T. Displacement is a vector quantity, meaning it has both magnitude and direction, which is crucial in understanding the overall motion of an object.
💡instantaneous rate of change
The instantaneous rate of change is the derivative's value at a specific point on a function, indicating the rate at which a quantity changes at that particular instant. In the context of the video, it is used to describe the velocity and acceleration of a moving object. For example, the instantaneous rate of change of position gives the velocity, and the instantaneous rate of change of velocity gives the acceleration.
💡speed
Speed is a scalar quantity that represents the magnitude of velocity, indicating how fast an object is moving without considering the direction. It is always positive, whereas velocity can be negative, indicating the direction of motion. Speed is used to describe the rate at which distance is covered by an object over time.
💡kinematics
Kinematics is a branch of physics that deals with the motion of objects without considering the forces that cause the motion. It involves the study of quantities such as position, velocity, and acceleration. The video's discussion of the relationship between position, velocity, and acceleration is a fundamental aspect of kinematics.
💡mechanical problem
A mechanical problem in the context of the video refers to a physics problem that involves the application of concepts from mechanics, such as the relationship between position, velocity, and acceleration. These problems often involve calculating the motion of an object under various conditions and are used to demonstrate the practical application of kinematic equations.
💡antiderivative
An antiderivative, also known as an integral, is the reverse process of differentiation. It is used to find the original function from its derivative. In the video, the concept of antiderivatives is mentioned in the context of understanding how to move from acceleration back to position and velocity, by integrating the acceleration function to find the velocity function, and then integrating the velocity function to find the position function.
💡slope of the tangent line
The slope of the tangent line to a function at a particular point is the value of the derivative at that point. It represents the instantaneous rate of change of the function at that specific location. In the context of the video, the slope of the tangent line to the position function corresponds to the velocity of the object at that point in its path.
Highlights

The relationship between position, velocity, and acceleration is based on derivatives.

The derivative of position gives you an equation that describes velocity.

The derivative of velocity provides the acceleration.

Position is often abbreviated as s(T), representing a function of time.

Velocity has a sign associated with it, indicating direction of movement.

Speed is always positive, as it is the absolute value of velocity.

The second derivative of the position function gives the acceleration.

A mechanical problem is used to illustrate the concepts with a particle moving in a straight line.

The equation of motion for the particle is s = 5T^3 + 3T + 8, where T is time in seconds.

The velocity after two seconds is calculated by taking the derivative of the position function and plugging in T = 2.

The velocity is found to be 63 meters per second after two seconds.

To find when the velocity equals 100 meters per second, the velocity equation is set to 100 and solved for T.

The acceleration is calculated by taking the derivative of the velocity function.

The acceleration after two seconds is found to be 60 meters per second squared.

Derivatives quantify the instantaneous rate of change, which can be useful in physical situations.

The speedometer in a car shows the instantaneous rate of change of distance, which is speed.

The slope of the tangent line in a position-time graph represents velocity.

Understanding the physical meaning behind derivatives makes calculus more useful and less mechanical.

Transcripts

Browse More Related Video

Worked example: motion problems (with definite integrals) | AP Calculus AB | Khan Academy

AP Calculus AB - Straight Line Motion

Graphing Motion

13 - Instantaneous Acceleration Explained (Average Vs. Instantaneous Acceleration)

Higher Order Derivatives (Part 2)

AP Physics Workbook 1.G Graphs of Velocity

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsCalculus ApplicationsMotion AnalysisDerivatives ExplainedInstantaneous RateVelocity CalculationAcceleration DerivationMechanical ProblemsEducational ContentMathematical Principles