11 - What is Definition of Average Speed & Velocity in Physics? (Speed Formula & Velocity Formula)
TLDRThis transcript delves into the nuances between average speed and average velocity in physics. It clarifies that while both concepts are related and measure the rate of motion, they differ in that speed lacks direction, making it a scalar quantity, whereas velocity includes direction, qualifying it as a vector. The lesson uses examples and analogies, such as car speedometers and number lines, to illustrate how distance, displacement, and time intervals determine these quantities. It emphasizes that average speed is always positive and doesn't indicate direction, while average velocity can be negative, reflecting the direction of travel.
Takeaways
- 🚗 Speed and velocity are distinct concepts in physics, with speed being the distance traveled per unit of time and velocity accounting for both distance and direction.
- 📏 Average speed is calculated as the total distance traveled divided by the time taken, and it is always a positive value since distance is always positive and time is always moving forward.
- 📐 Average velocity is calculated as displacement (change in position) divided by the time interval, and it can be positive or negative, indicating the direction of motion.
- 🔄 The difference between speed and velocity lies in the fact that speed does not convey direction, whereas velocity does, making velocity a vector quantity.
- 🌐 In everyday language, speed and velocity are often used interchangeably, but in physics, they have precise and different meanings.
- 🕒 Time intervals in physics are always positive as time only moves forward, affecting the calculation of both speed and velocity.
- 📊 The sign of average velocity indicates the direction of motion, with positive values indicating movement to the right and negative values indicating movement to the left.
- 🔢 Average speed is the magnitude of the average velocity, disregarding the direction, and is thus always positive.
- 📈 The concepts of average speed and velocity are crucial for understanding motion and will be further explored in conjunction with vectors in physics.
- 🔄 The average velocity does not account for variations in speed during the time interval; it only considers the total displacement and total time.
- 🚀 Future lessons will delve into instantaneous velocity, which provides a more detailed understanding of motion at a specific moment in time.
Q & A
What is the main difference between speed and velocity?
-Speed is a scalar quantity that represents the rate of motion, while velocity is a vector quantity that includes both the rate of motion and the direction of movement.
How is average speed calculated?
-Average speed is calculated by dividing the total distance traveled by the total time taken, resulting in a value that is always positive since both distance and time intervals are positive quantities.
What is the formula for average velocity?
-The formula for average velocity is the displacement (change in position) divided by the time interval. It can be represented as Δx/Δt, where Δx is the change in position and Δt is the change in time.
Why is average velocity considered a vector quantity?
-Average velocity is considered a vector quantity because it includes information about both the magnitude and the direction of the movement, allowing it to have a positive or negative value depending on the direction of travel.
How does the average speed differ from the instantaneous speed?
-Average speed gives the overall rate of motion over a period of time, while instantaneous speed refers to the speed of an object at a specific moment in time.
What is the significance of the sign in the average velocity calculation?
-The sign in the average velocity calculation indicates the direction of travel. A positive value means movement to the right or in the positive direction, while a negative value indicates movement to the left or in the negative direction.
Can you provide an example of how to calculate average speed?
-If an object travels 10 meters in 2 seconds, the average speed is calculated as 10 meters divided by 2 seconds, resulting in 5 meters per second (m/s).
Can you provide an example of how to calculate average velocity?
-If an object moves from an initial position of -2 meters to a final position of +2 meters in 1 second, the average velocity is calculated as the displacement (+2 - (-2)) divided by the time interval (1 second), resulting in 4 meters per second (m/s) with a positive sign indicating the direction of travel.
What is the relationship between distance and displacement?
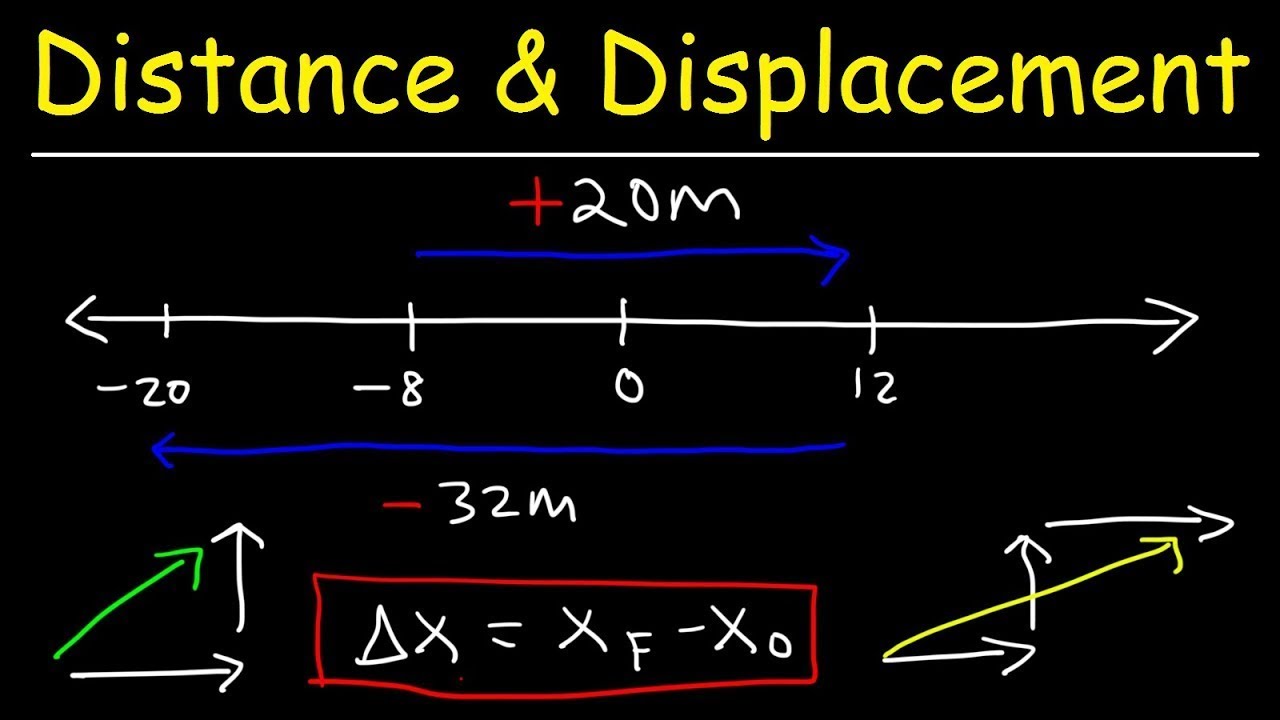
-Distance is the total length of the path traveled by an object, while displacement is the straight-line distance between the starting and ending points, including the direction of travel. Distance can be greater than or equal to displacement, but it never includes directional information.
How does the concept of vectors apply to physics problems?
-Vectors are essential in physics because they provide both magnitude and direction, which are crucial for accurately describing and solving problems involving motion, forces, and other physical quantities that have both size and direction.
Why is it important to distinguish between speed and velocity in physics?
-Distinguishing between speed and velocity is important because it allows for a more precise understanding of motion. While speed tells you how fast something is moving, velocity provides additional information about the direction of that motion, which is necessary for analyzing and predicting the behavior of objects in motion.
Outlines
📚 Introduction to Average Speed and Velocity
This paragraph introduces the concepts of average speed and velocity, highlighting the common misconception that they are interchangeable. It explains that while they are related, they are not the same, emphasizing the difference between speed (a scalar quantity) and velocity (a vector quantity). The explanation includes a review of the previous lesson on distance and displacement, noting that average speed is always positive as it is derived from dividing a positive distance by a positive time interval, thus lacking directional information.
📐 Calculating Average Speed and Velocity
The paragraph delves into the formulas for calculating average speed and velocity. It clarifies that average speed is the total distance traveled divided by the time taken, resulting in a positive value since both distance and time intervals are positive. In contrast, average velocity considers displacement, which can be positive or negative, and the time interval, which is always positive. This results in velocity being a vector quantity that indicates both magnitude and direction, unlike speed, which only indicates how fast an object is moving without direction.
🔄 Understanding the Difference: Speed vs. Velocity
This section reinforces the difference between speed and velocity with examples and further explanations. It uses a number line to illustrate how the direction of movement affects the calculation of average velocity, which can be positive or negative depending on the direction. The paragraph also explains that while speed is always positive, velocity can have a negative value, indicating movement in the opposite direction. The importance of understanding these differences is emphasized, especially in scenarios like collisions where the direction of velocity is crucial.
🕒 Time and Distance in Average Velocity and Speed
The paragraph discusses the impact of time and distance on the calculation of average velocity and speed. It explains that average velocity is determined by the change in position (displacement) over the change in time, which can result in various outcomes depending on the direction of movement and the time interval. The example provided illustrates how different paths and rates of speed over time can result in the same average velocity, as it only considers the initial and final positions and the time taken, without accounting for the specifics of the motion between these points.
🌟 Average vs. Instantaneous: A Preview of Future Concepts
In this concluding paragraph, the script introduces the idea of instantaneous velocity, which will be explored in more detail in future lessons. It contrasts this with average velocity, explaining that while average velocity provides an overall view of motion over a period of time, instantaneous velocity focuses on the specific speed of an object at a particular moment within that time interval. The paragraph sets the stage for a deeper dive into the concepts of vectors and motion, promising a comprehensive exploration of these topics in upcoming lessons.
Mindmap
Keywords
💡Average Speed
💡Average Velocity
💡Displacement
💡Distance
💡Time Interval
💡Vector
💡Scalar
💡Direction
💡Physics
💡Motion
Highlights
Speed and velocity are distinct concepts in physics, despite being often used interchangeably in everyday language.
Speed is a scalar quantity that represents the rate of motion, calculated as distance traveled divided by the time taken, and is always positive.
Velocity, on the other hand, is a vector quantity that includes both the rate of motion and the direction of travel.
The average speed is calculated by dividing the total distance traveled by the total time taken, resulting in a positive value since both distance and time intervals are positive.
Average velocity is calculated using displacement (change in position) over the time interval, which can result in either a positive or negative value, indicating direction.
Displacement is defined as a vector because it includes information about both the magnitude and direction of movement.
The difference between distance and displacement is that distance is always positive and does not include directional information, whereas displacement can be positive or negative depending on the direction of travel.
An example given in the transcript explains that if an object travels 10 meters in 2 seconds, its average speed is 5 meters per second.
For an object moving from an initial position of -2 meters to a final position of +2 meters in 1 second, the average speed is 4 meters per second.
The average velocity can convey the direction of movement, as it is a vector quantity, while average speed cannot, as it is a scalar quantity.
In a hypothetical scenario, an object moving from an initial position of -4 meters to a final position of +2 meters in 3 seconds has an average velocity of 2 meters per second to the right.
The average speed in the same scenario would also be 2 meters per second, as the sign is disregarded when calculating speed.
Understanding the difference between average speed and average velocity is crucial for accurately analyzing and predicting the motion of objects.
The concept of average velocity assumes a constant rate of motion between the initial and final positions, without considering any variations in speed during the interval.
Instantaneous velocity, which will be covered later in the course, provides a more detailed analysis of motion by considering the speed at any given moment, rather than just the average.
All velocities, displacements, and forces are vectors, which will be explored in more detail in subsequent lessons.
Transcripts
Browse More Related Video
Distance, Displacement, Average Speed, Average Velocity - Physics

What is Velocity? Physics

What is Velocity? - Full Concept of Velocity - Physics | Infinity Learn

What Are Speed and Velocity? | Physics in Motion

Distance vs. Displacement & Speed vs. Velocity | Kinematics Explained
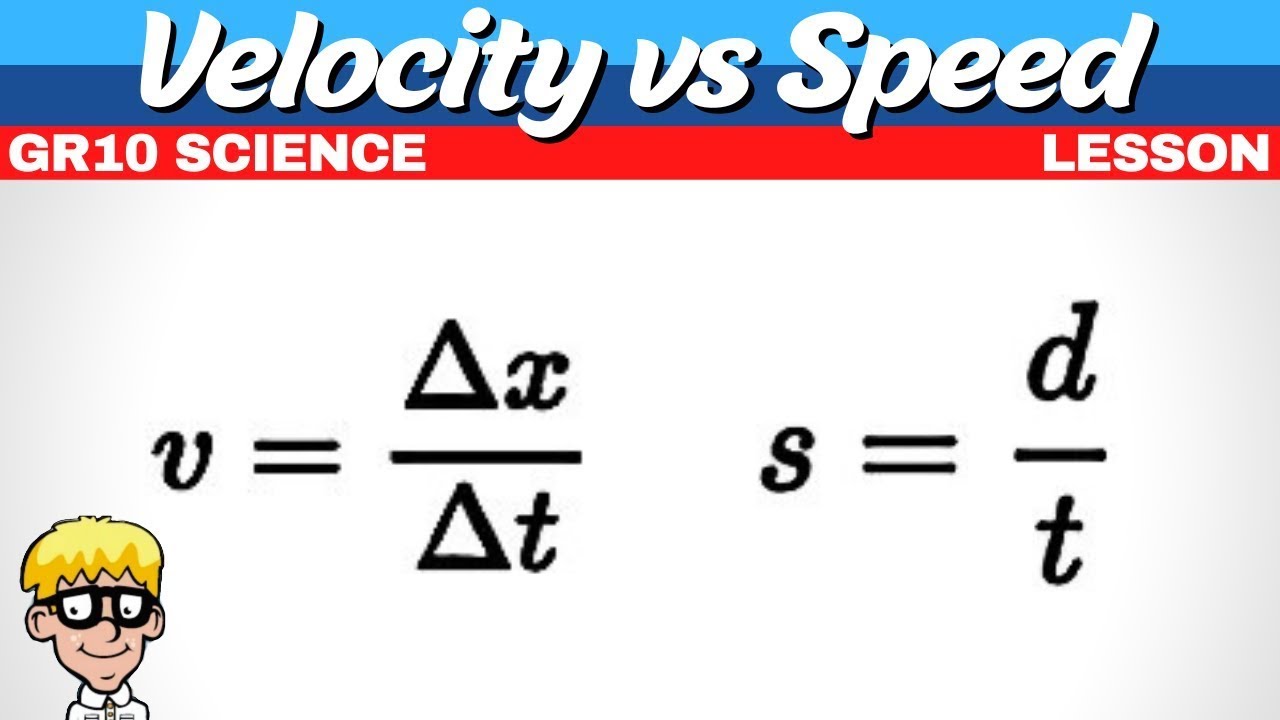
Velocity vs Speed Grade 10 Science
5.0 / 5 (0 votes)
Thanks for rating: