Statistics: Sample variance | Descriptive statistics | Probability and Statistics | Khan Academy

Khan Academy
22 Jan 200911:17
EducationalLearning
32 Likes 10 Comments

TLDRThis video script introduces the concept of variance, both for a population and a sample, with an emphasis on the importance of understanding the difference between the two. The presenter explains the formula for calculating variance and highlights the common mistake of using the sample variance formula without adjusting for bias, which can lead to an underestimation of the true population variance. The script also discusses the notion of an 'unbiased' sample variance estimate, which divides by n-1 instead of n, providing a more accurate reflection of the population variance.

Takeaways
  • 📚 The video introduces the concept of variance, specifically for a sample, which is a fundamental statistical measure.
  • 🎥 The presenter is attempting to record the video in HD for better clarity, making this an experimental video.
  • 📈 The variance of a population is denoted by the Greek letter sigma (σ) squared, representing the average of squared distances from the mean.
  • 🔍 The variance measures how far each point in the data set is, on average, from the mean, indicating the spread of the data.
  • 🌐 The script discusses the impracticality of calculating the variance for an entire population, such as the heights of all men in a country.
  • 🔬 Often, the variance of a sample is used to estimate the variance of a population, a common practice in inferential statistics.
  • 📝 The mean of a population is calculated by summing all data points and dividing by the number of points (N).
  • 📉 The natural inclination might be to apply the same formula for variance to a sample, but this can lead to an underestimation.
  • 🤔 The presenter discusses the intuition behind why the sample variance might underestimate the population variance, especially if the sample mean is not representative of the population mean.
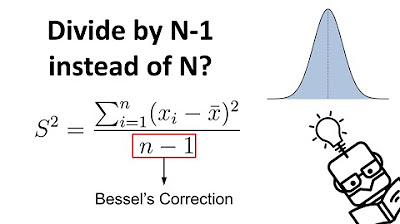
  • 📊 An unbiased estimator for the population variance is given by dividing the sum of squared distances by (n - 1) instead of (n), which provides a better estimate.
  • 🔮 The video promises to demonstrate the effectiveness of the unbiased estimator in a future video with calculations and possibly a computer program.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the concept of variance, specifically the variance of a sample and its relationship to the variance of a population.

  • What is the symbol used to represent the variance of a population?

    -The Greek letter sigma, lowercase sigma squared (σ²) is used to represent the variance of a population.

  • How is the variance of a population calculated?

    -The variance of a population is calculated by taking each data point, finding its squared distance from the mean of the population, and then taking the average of all these squared distances.

  • What is the difference between the variance of a population and the sample variance?

    -The variance of a population is calculated using the entire dataset, while the sample variance is an estimate of the population variance based on a subset of the data.

  • Why might the sample variance underestimate the actual population variance?

    -The sample variance might underestimate the actual population variance because the sample mean is always within the sample data and may not accurately represent the population mean, leading to smaller squared distances in the calculation.

  • What is an unbiased estimate of the population variance?

    -An unbiased estimate of the population variance is calculated by dividing the sum of squared distances of each data point from the sample mean by n - 1 instead of n, where n is the number of data points in the sample.

  • What is the notation used for the sample mean?

    -The sample mean is denoted by χ, which is the average of all data points in the sample.

  • What is the purpose of using a sample to estimate population statistics?

    -Using a sample to estimate population statistics allows for the analysis of large or inaccessible populations without needing to measure every individual within the population.

  • Why is it important to understand the difference between a sample and a population in statistics?

    -Understanding the difference between a sample and a population is crucial for making accurate inferences about the population based on sample data, which is a fundamental concept in inferential statistics.

  • What does the video suggest about the relationship between the sample mean and the population mean?

    -The video suggests that while the sample mean can be a good estimate of the population mean, there is always a chance that the sample mean does not accurately represent the population mean, especially if the sample is skewed or not representative of the population.

  • What is the significance of the video attempting to be recorded in HD?

    -The significance of attempting to record the video in HD is to provide a clearer and more detailed visual experience for the viewers, enhancing their understanding of the complex statistical concepts being discussed.

Outlines
00:00
📚 Introduction to Variance and HD Video Experiment

The speaker introduces the topic of variance, both for a population and a sample, and discusses the experiment of recording the video in HD for better clarity. The variance of a population is explained using the Greek letter sigma (σ²) to represent it, and the formula involves taking each data point (xi), calculating its squared distance from the population mean, and averaging these values. The concept of variance is further clarified as the average squared distance of each point from the mean, which gives an idea of the data's dispersion. The video also touches on the impracticality of measuring the entire population's variance, such as the heights of all men in a country, and the necessity of estimating it through a sample variance, which is foundational in inferential statistics.

05:01
🔍 Understanding Sample Variance and Its Pitfalls

This paragraph delves deeper into the concept of sample variance, contrasting it with the population variance. The speaker explains that while the formula for calculating sample variance seems straightforward—using the sample mean and averaging the squared distances of each point from it—there's a potential issue. The issue arises because the sample mean is always within the sample and may not accurately represent the population mean, which could be outside the sample range. This discrepancy can lead to an underestimation of the actual population variance. The speaker illustrates this with a hypothetical scenario involving the selection of data points and the impact of sample skewness on variance calculation. The paragraph concludes with the acknowledgment that grasping these concepts is a significant achievement for any student of statistics.

10:02
📉 Unbiased Estimation of Population Variance

The final paragraph introduces the concept of an unbiased estimate of the population variance, which is a more accurate way to calculate sample variance. The speaker explains that the standard sample variance formula can underestimate the true variance because it divides by the number of data points (n), which can be improved by dividing by n-1 instead. This adjustment provides a better approximation of the population variance, as it accounts for the reduced degrees of freedom in a sample. The speaker expresses an intention to experimentally verify this through a computer program in a future video and concludes the current discussion, promising to demonstrate calculations in the next video to solidify the understanding of these abstract concepts.

Mindmap
Keywords
💡Variance
Variance is a statistical measure that quantifies the dispersion of a set of data points around their mean value. In the video, variance is introduced as a key concept for understanding the spread of data in a population and a sample. The script explains that variance is calculated by taking the average of the squared differences from the mean, which gives an idea of how data points are spread out. For example, the script states, 'The variance is the average of the squared distances, of each point from the mean.'
💡Sample
A sample is a subset of a population that is taken to represent the whole group for statistical analysis. The video discusses the concept of a sample in the context of estimating population parameters like mean and variance when it is impractical to measure the entire population. The script mentions, 'a lot of times, you actually want to estimate this variance by taking, the variance of a sample,' highlighting the importance of samples in inferential statistics.
💡Population
A population in statistics refers to the entire set of individuals or data points that are the subject of a study. The video script contrasts the population with a sample, explaining that while the population variance is calculated using all data points, it may be impractical to obtain. For instance, the script states, 'The variance of a population...you take each data point and find out how far it is from the mean of the population.'
💡Mean
The mean, often referred to as the average, is the sum of all data points in a set divided by the number of points. The video script explains how to calculate the mean for both a population and a sample, and how it serves as a central value from which deviations are measured to calculate variance. The script illustrates this by saying, 'The mean of a population, you just take each of the data points in the population...and you divide by N.'
💡Sigma (σ)
Sigma, represented by the Greek letter σ, is used in statistics to denote the standard deviation of a set of values, which is the square root of variance. In the script, sigma is introduced as part of the notation for variance (σ²), indicating the squared standard deviation of a population. The script points out, 'And it's, this Greek letter, sigma. Lowercase sigma squared. That means variance.'
💡Estimate
An estimate in statistics is a value that is used to approximate an unknown parameter based on a sample. The video script discusses estimating the population mean and variance through sample statistics, which is a fundamental concept in inferential statistics. The script mentions, 'So a lot of times, you actually want to estimate this variance by taking, the variance of a sample.'
💡Unbiased Sample Variance
Unbiased sample variance is a statistical calculation that provides an estimate of the population variance without being systematically lower or higher than the true value. The video script introduces an adjusted formula for sample variance (s² with n-1 in the denominator) that is considered an unbiased estimator of the population variance. The script explains, 'And there's a formula...that is considered to be a better...unbiased estimate of the population variance.'
💡Inferential Statistics
Inferential statistics involves using data from a sample to make inferences about a population. The video script explains that inferential statistics is about estimating population parameters like mean and variance from sample statistics, which is crucial when the entire population cannot be measured. The script states, 'This is actually what most of inferential statistics is all about. Figuring out descriptive statistics about the sample, and making inferences about the population.'
💡Random Sample
A random sample is a subset of a population where each member has an equal chance of being selected. The video script emphasizes the importance of random sampling to avoid bias and ensure that the sample can represent the population accurately. The script mentions, 'You actually want to take a random sample. You don't want to be skewed in any way.'
💡Experimental
In the context of the video, experimental refers to the process of testing or trying out a new method or approach, such as recording the video in HD to see if it improves clarity. The script mentions, 'But we'll see how all of that goes. So this is a bit of an experiment, so bear with me.'
Highlights

Introduction to the concept of variance for a sample, a fundamental statistical measure.

Attempt to record the video in HD for improved clarity, an experimental approach to video production.

Review of population variance formula using lowercase sigma squared (σ²) to denote variance.

Explanation of variance as the average of squared distances of each data point from the mean.

Discussion on the impracticality of measuring the variance of an entire population, such as men's heights in a country.

Introduction of sample variance as an estimation method for population variance when the entire data set is inaccessible.

Differentiation between descriptive statistics for a sample and inferential statistics about a population.

Illustration of the concept of sample versus population and the importance in statistical inference.

Formula for calculating the mean of a population and its significance in understanding variance.

Transition from population mean to sample mean in the context of variance calculation.

Misinterpretation of sample variance as an underestimate of the population variance due to the sample mean's proximity to data points.

The problem with using sample size (n) as the denominator when calculating sample variance, potentially leading to an underestimation.

Introduction of an unbiased estimator for population variance, using n-1 as the denominator instead of n.

Explanation of why dividing by n-1 instead of n provides a better estimate of the population variance.

Acknowledgment of the abstract nature of the topic and the plan to demonstrate the concepts with calculations in the next video.

The importance of understanding the difference between sample variance and population variance for accurate statistical analysis.

Transcripts

Browse More Related Video

Review and intuition why we divide by n-1 for the unbiased sample | Khan Academy

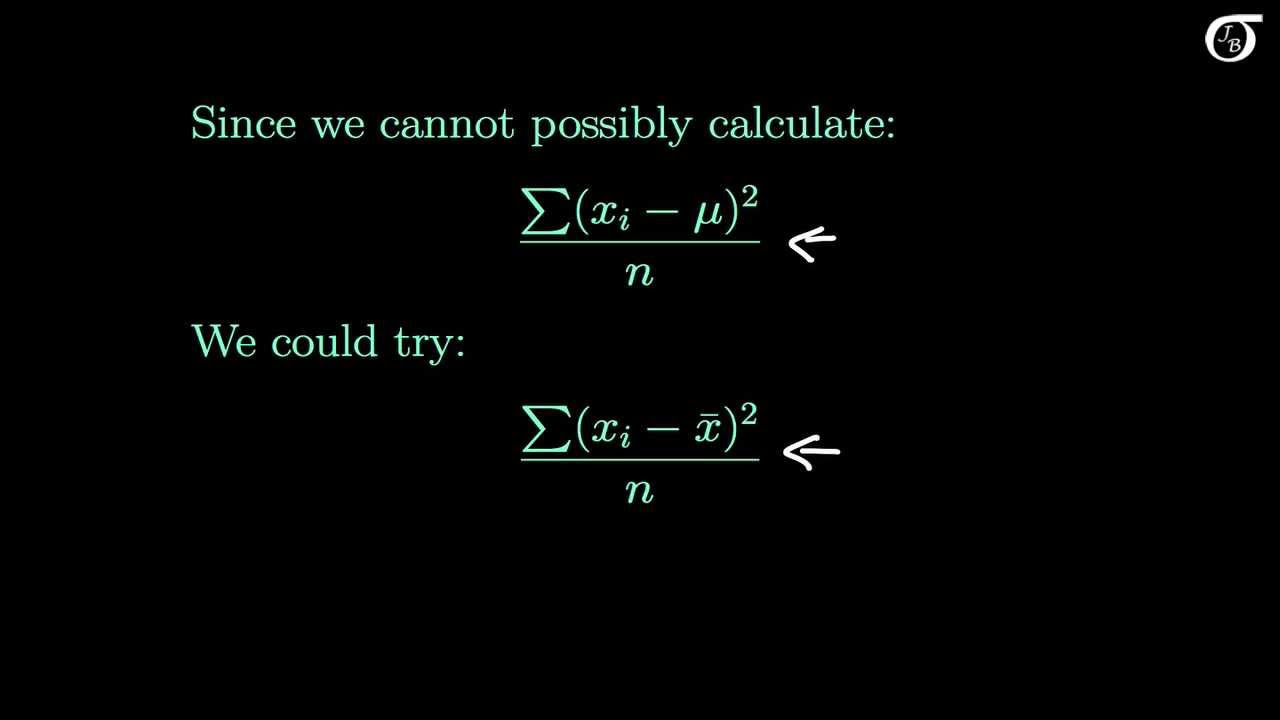
The Sample Variance: Why Divide by n-1?

Simulation showing bias in sample variance | Probability and Statistics | Khan Academy

Why We Divide by N-1 in the Sample Variance (Standard Deviation) Formula | The Bessel's Correction

Why do we divide by n-1 and not n? | shown with a simple example | variance and sd

Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
VarianceSamplePopulationStatisticsTutorialMeanEstimationInferentialExperimentEducationalHD Video