Simulation showing bias in sample variance | Probability and Statistics | Khan Academy
TLDRThe video script explains a simulation by Peter Collingridge using the Khan Academy's computer science scratch pad to illustrate the concept of unbiased sample variance. The simulation constructs a random population distribution and calculates its parameters, including the mean and variance. It then samples from this population with varying sizes and calculates the biased sample variance. The script highlights that smaller sample sizes tend to underestimate the variance and have sample means far from the population mean. The simulation demonstrates that the biased sample variance approaches a fraction of the true population variance, where the fraction is n/(n-1), with n being the sample size. To obtain an unbiased estimate of the population variance, the biased variance should be multiplied by (n/(n-1)), which aligns with the formula taught in statistics for an unbiased sample variance. The script aims to provide intuition and clarity on why dividing by n-1 is used in the calculation of unbiased sample variance.
Takeaways
- 🌟 The simulation by Peter Collingridge on the Khan Academy computer science scratch pad is designed to illustrate why we divide by (n - 1) when calculating an unbiased sample variance for estimating the true population variance.
- 🔍 The simulation constructs a random population distribution each time it is run, providing a unique set of data for analysis.
- 📊 It calculates the mean and variance directly from the population, which serves as the basis for subsequent sampling and variance calculations.
- 🧐 The biased sample variance is calculated by dividing the sum of squared differences from the sample mean by (n), rather than (n - 1).
- 📉 The simulation reveals that samples with means far from the true population mean tend to underestimate the variance, particularly when sample sizes are small.
- 🔵 Larger sample sizes, represented by bluer dots, tend to provide better estimates of the population variance, while smaller sample sizes, represented by red dots, are more likely to underestimate it.
- 📌 The biased sample variances for different sample sizes approach fractions of the true population variance (1/2 for (n = 2), 2/3 for (n = 3), etc.).
- 🔄 To correct for bias and obtain an unbiased estimate of the population variance, the biased variance should be multiplied by (n/(n - 1)).
- ⚖️ Dividing by (n - 1) instead of (n) in the calculation of sample variance is crucial for obtaining an unbiased estimate of the population variance.
- 📈 The simulation provides an intuitive understanding of why the bias occurs and how the correction factor addresses it, which can be a confusing concept in statistics.
- 📚 Peter's simulation can be a valuable educational tool for those studying statistics, helping to clarify the rationale behind using (n - 1) in variance calculations.
Q & A
What is the purpose of the simulation created by Peter Collingridge?
-The simulation was created to better understand why we divide by n minus one when calculating an unbiased sample variance, which is essential when estimating the true population variance in a statistically unbiased way.
How does the simulation construct the population distribution?
-The simulation constructs a random population distribution each time it is run, resulting in a different distribution every time.
What are the parameters calculated directly from the population in the simulation?
-The simulation calculates the mean and variance of the population directly from the distribution.
What sample sizes does the simulation use for its calculations?
-The simulation uses sample sizes ranging from two to ten.
What is the difference between a biased and an unbiased sample variance?
-A biased sample variance is calculated by dividing the sum of squared differences from the sample mean by the sample size (n), which tends to underestimate the true population variance. An unbiased sample variance divides by n minus one, providing a better estimate of the population variance.
How does the simulation provide intuition about the relationship between sample mean and variance?
-The simulation shows that when the sample mean is significantly different from the true mean, the sample variance is likely to be underestimated. This relationship is visually represented in the simulation's graphs.
What does the color coding in the simulation represent?
-The color coding represents the sample size, with pinker dots indicating smaller sample sizes and bluer dots indicating larger sample sizes.
Why is it more likely to underestimate the sample variance with a smaller sample size?
-With a smaller sample size, there is a higher probability of the sample mean being a poor estimate of the population mean, which in turn leads to a significant underestimation of the sample variance.
What does the second chart in the simulation demonstrate?
-The second chart demonstrates that the biased sample variance divided by the population variance approaches a fraction of the true population variance based on the sample size, such as 1/2 for n=2, 2/3 for n=3, and 3/4 for n=4.
How can the biased estimate of the population variance be corrected to be unbiased?
-To correct the biased estimate, you multiply the biased sample variance by n/(n-1), which results in an unbiased estimate of the population variance.
What is the significance of dividing by n minus one in the calculation of unbiased sample variance?
-Dividing by n minus one corrects the bias in the estimation of the population variance from a sample, providing a more accurate reflection of the true variance in the population.
How does Peter Collingridge's simulation help in understanding the concept of unbiased sample variance?
-The simulation provides a visual and interactive way to observe how different sample sizes and the resulting sample means affect the variance calculation. It helps to illustrate why dividing by n minus one, rather than n, leads to an unbiased estimate of the population variance.
Outlines
📊 Understanding Unbiased Sample Variance Calculation
This paragraph explains a simulation created by Peter Collingridge using the Khan Academy's computer science scratch pad to illustrate the concept of dividing by n-1 when calculating an unbiased sample variance. The simulation generates a random population distribution and calculates its parameters, such as the mean and variance. It then samples from this population with varying sizes and calculates the sample mean and variance, focusing on the biased sample variance calculation. The paragraph discusses how the biased variance underestimates the true variance, especially when the sample mean significantly deviates from the population mean. It also highlights that smaller sample sizes are more likely to yield poor estimates of the population mean and variance. The simulation provides visual data points to study these relationships in detail, with the conclusion that the biased variance tends to approach n-1/n times the population variance, leading to the insight that dividing by n-1 provides an unbiased estimate.
🔍 Correcting Bias in Sample Variance Estimation
The second paragraph delves into the issue of bias in the estimation of population variance from a sample. It outlines how the biased sample variance, calculated by dividing by n instead of n-1, results in an estimate that is a fraction of the true population variance. The paragraph presents a progression: for a sample size of two, the biased estimate approaches half of the population variance; for three, it's two-thirds; and for four, it's three-quarters. To obtain an unbiased estimate, the paragraph suggests multiplying the biased estimate by n/(n-1), which cancels out the bias, leaving the true population variance. This process aligns with the formulas and concepts typically found in statistics books, and the paragraph reinforces the rationale behind using n-1 in the denominator for calculating an unbiased sample variance.
Mindmap
Keywords
💡Unbiased Sample Variance
💡Population Distribution
💡Sample Size
💡Biased Sample Variance
💡Sample Mean
💡Khan Academy
💡Peter Collingridge
💡Estimation
💡Variance
💡Simulation
💡n Minus One
Highlights
The simulation constructs a random population distribution each time it is run, with different parameters like population size, mean, and variance.
The simulation samples from the population with sizes ranging from 2 to 10, calculating sample mean and variance for each.
The biased sample variance is calculated by dividing by n (sample size) instead of n-1.
When the sample mean is far off from the true mean, the sample variance is significantly underestimated.
Smaller sample sizes (pink dots) are more likely to underestimate variance and have sample means far from the true mean.
Larger sample sizes (blue dots) provide better estimates of variance and are less likely to deviate from the true mean.
The biased sample variance divided by the population variance approaches n/(n-1) as the sample size increases.
For sample size 2, the biased variance is about 1/2 of the true population variance. For size 3, it's about 2/3.
The biased estimate does not converge to the population variance as sample size increases.
To obtain an unbiased estimate of the population variance, multiply the biased variance by n/(n-1).
The unbiased sample variance formula is the one commonly used in statistics, dividing by n-1 instead of n.
The simulation provides intuition and convinces us of why dividing by n-1 is necessary for an unbiased estimate.
The simulation allows users to zoom in and study the graphs in detail to better understand the concepts.
The population mean and variance are plotted on the first chart, with sample means and variances shown for different sample sizes.
The color of the dots in the chart indicates sample size, with pink for smaller sizes and blue for larger sizes.
The simulation demonstrates the relationship between sample size, sample mean accuracy, and the bias in sample variance estimation.
The biased variance converges to different fractions of the true variance depending on the sample size, highlighting the need for correction.
The simulation helps clarify why the unbiased sample variance formula divides by n-1 rather than n.
Transcripts
Browse More Related Video
Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance

Simulation providing evidence that (n-1) gives us unbiased estimate | Khan Academy

Review and intuition why we divide by n-1 for the unbiased sample | Khan Academy

Why do we divide by n-1 and not n? | shown with a simple example | variance and sd
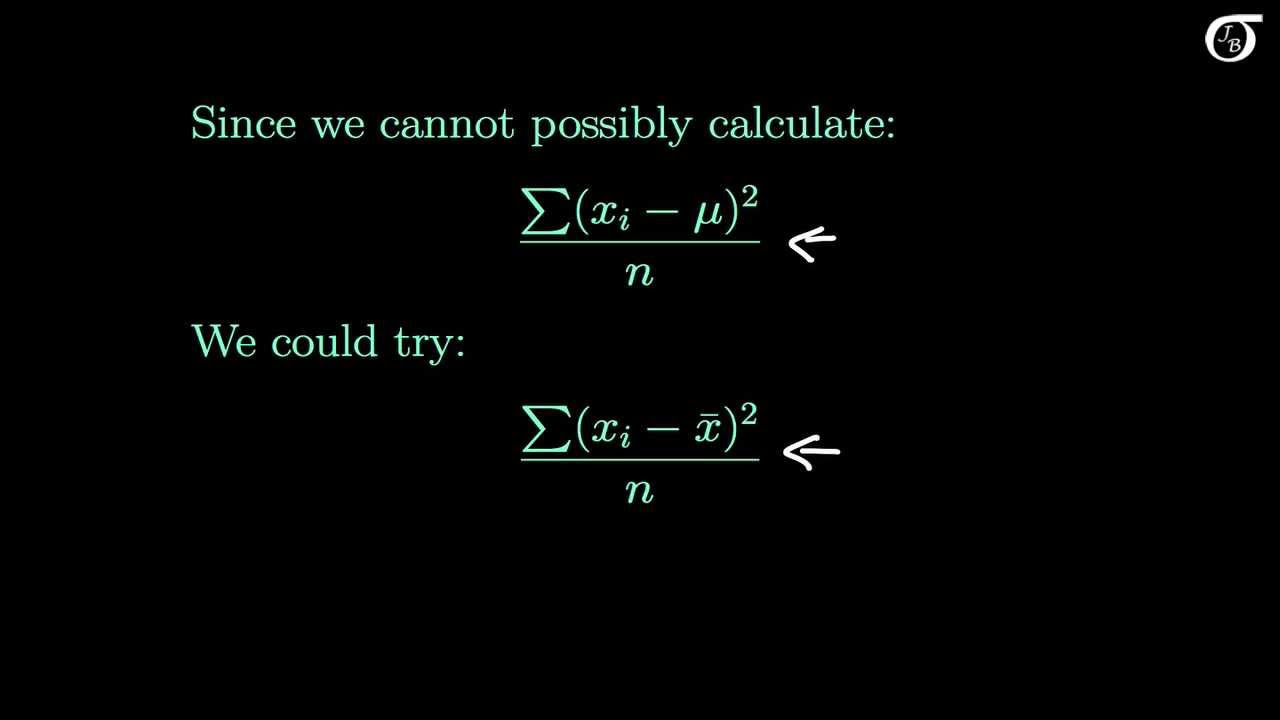
The Sample Variance: Why Divide by n-1?
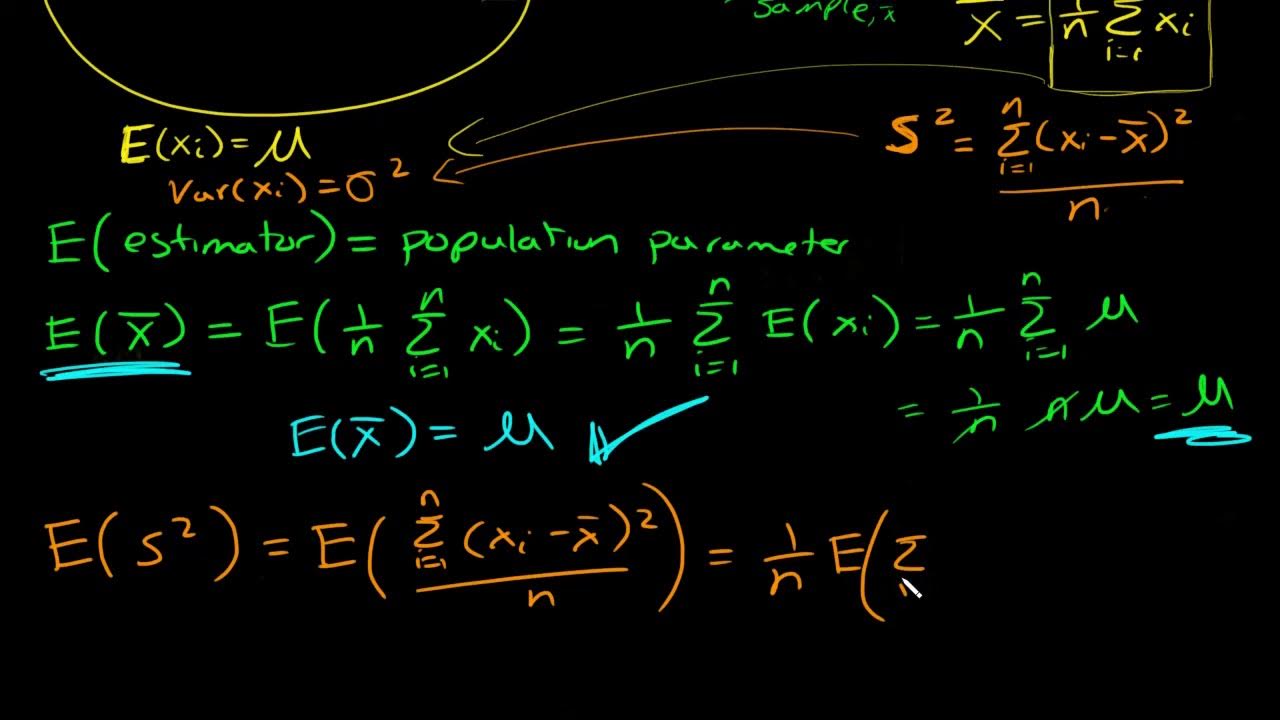
What is an unbiased estimator? Proof sample mean is unbiased and why we divide by n-1 for sample var
5.0 / 5 (0 votes)
Thanks for rating: