Free Fall Physics Problems - Acceleration Due To Gravity
TLDRThe transcript explores the principles of free fall and acceleration due to gravity, demonstrating that in the absence of air resistance, objects of different masses fall at the same rate. It uses examples like the 10-gram and 5-gram metal balls to illustrate this concept. The script further explains how air resistance affects objects with different surface areas, using the brick versus flat paper example. It delves into the physics equations needed to calculate displacement and distance traveled during free fall, and applies these concepts to solve problems involving falling objects from various heights and initial velocities, ultimately providing insights into the time taken to fall and the final speed of the objects.
Takeaways
- 📈 In free fall, objects regardless of their mass reach the ground at the same time when air resistance is negligible.
- 🎾 The acceleration due to Earth's gravity is 9.8 meters per second squared, affecting all objects equally in the absence of air resistance.
- 🧱 A heavier object like a brick and a lighter one like a flat piece of paper will hit the ground at different times if air resistance is considered.
- 🏋️♂️ When air resistance is significant, the surface area of an object greatly affects the rate at which it falls.
- 🔢 The velocity of an object in free fall increases by 9.8 meters per second every second, while the speed increases but the velocity, being negative, decreases by the same amount.
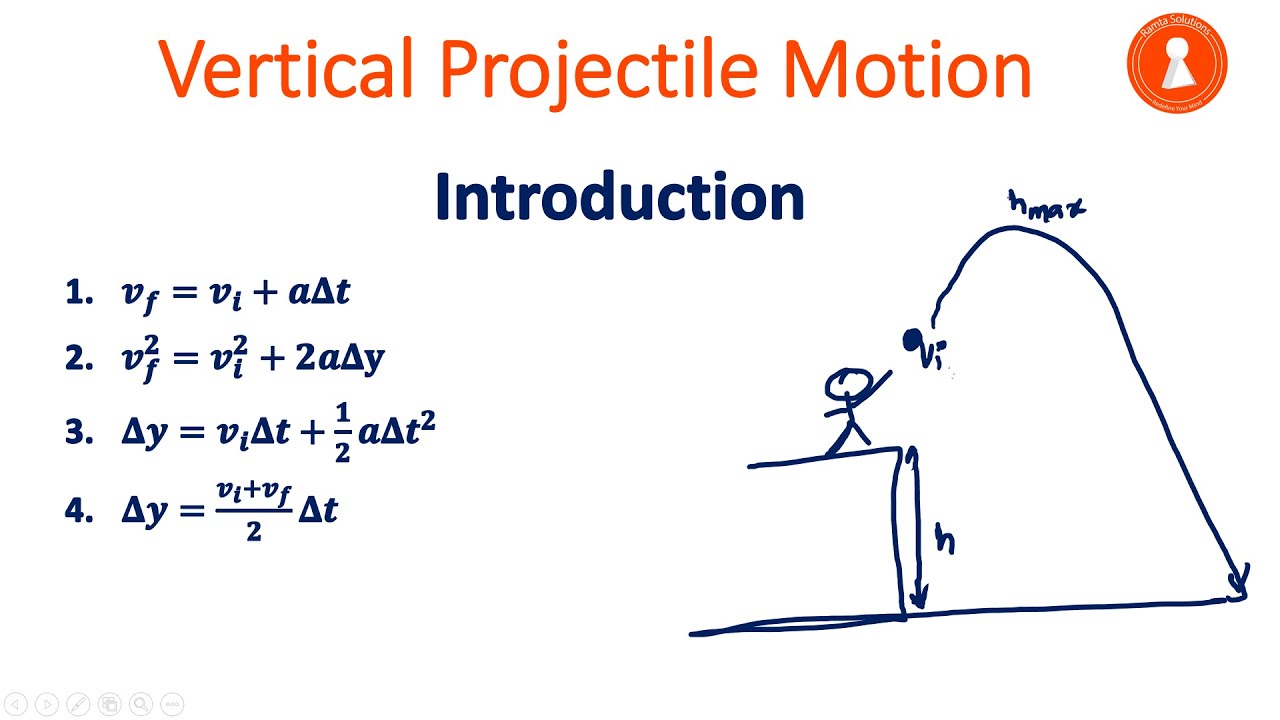
- 📐 The key equations for constant acceleration motion include: v = u + at, s = ut + 0.5at², and v² = u² + 2as.
- 🏢 To find the height of a building or cliff, the displacement (which is negative in the downward direction) can be calculated using the formula d = 0.5gt².
- 🚀 For an object thrown downward with an initial velocity, the final velocity and speed can be calculated using v = u + gt.
- 🕰️ The time it takes for an object to hit the ground can be found using the formula s = 0.5gt² when the initial speed is zero.
- 🏌️♂️ The distance traveled by a falling object is the absolute value of the displacement, which is always positive.
- 🔄 The concepts of speed and velocity are crucial in understanding motion, with speed being a scalar quantity and velocity being a vector quantity.
Q & A
Why do two balls of different masses fall at the same rate when dropped from the same height in a vacuum?
-In a vacuum, the absence of air resistance means that the only force acting on the balls is gravity. Since the gravitational force (weight) is proportional to mass and the acceleration due to gravity is constant, both balls experience the same acceleration regardless of their mass, leading to them hitting the ground simultaneously.
What is the acceleration due to gravity on Earth?
-The acceleration due to gravity on Earth is approximately 9.8 meters per second squared (9.8 m/s^2). This value represents the rate at which an object accelerates when in free fall near the Earth's surface.
How does air resistance affect the motion of falling objects with different shapes and masses?
-Air resistance affects the motion of falling objects by creating a drag force that opposes the motion. Objects with larger surface areas, like a flat piece of paper, experience more air resistance compared to objects with smaller surface areas, like a crumpled paper ball. Heavier objects, like a brick, are less affected by air resistance due to their higher inertia, and thus they fall more directly to the ground compared to lighter objects.
What is the relationship between speed and velocity?
-Speed is a scalar quantity that represents the rate of motion, without regard to direction, while velocity is a vector quantity that includes both the rate of motion and the direction of travel. Speed is always positive, whereas velocity can be positive or negative depending on the direction of motion.
How can you calculate the distance an object falls in free fall after a certain time?
-The distance an object falls in free fall can be calculated using the equation: d = 0.5 * a * t^2, where 'a' is the acceleration due to gravity (approximately -9.8 m/s^2) and 't' is the time in seconds. This equation assumes no air resistance and that the object starts from rest.
What is the final velocity of an object in free fall after a given time?
-The final velocity of an object in free fall after a certain time can be calculated using the formula: v = u + a*t, where 'u' is the initial velocity (0 if the object is dropped from rest), 'a' is the acceleration due to gravity (approximately -9.8 m/s^2), and 't' is the time in seconds.
How do you determine the height from which an object has fallen based on the time it takes to hit the ground?
-The height from which an object has fallen can be determined using the equation: h = 0.5 * g * t^2, where 'g' is the acceleration due to gravity (approximately 9.8 m/s^2) and 't' is the time in seconds it takes for the object to hit the ground. This calculation assumes that the object is in free fall without air resistance.
What is the difference between displacement and distance traveled?
-Displacement is a vector quantity that represents the change in position of an object and includes both the magnitude and direction of the movement. Distance traveled, on the other hand, is a scalar quantity that represents the total length of the path taken by the object, without considering direction.
How does the initial speed of an object affect its final velocity and displacement in free fall?
-The initial speed of an object affects both its final velocity and displacement. A non-zero initial speed adds to the velocity gained from acceleration due to gravity. The displacement is influenced by both the initial speed and the time the object is in motion, as it is calculated using the formula d = v_initial * t + 0.5 * a * t^2.
What is the significance of the negative sign in the equations of motion for free fall?
-The negative sign in the equations of motion for free fall indicates the direction of the motion and acceleration. Since objects fall downward (in the negative y-direction by convention), the acceleration due to gravity is considered negative (-9.8 m/s^2). However, speed is always positive because it is a scalar quantity and does not include direction.
How does the shape of an object influence its terminal velocity?
-Terminal velocity is the constant speed that a freely falling object eventually reaches when the resistance of the medium through which it is falling prevents further acceleration. The shape of an object significantly influences its terminal velocity because it affects the drag force acting on the object. A streamlined shape reduces air resistance, leading to a higher terminal velocity, while a flat or irregular shape increases air resistance, resulting in a lower terminal velocity.
Outlines
🌐 Principles of Free Fall and Gravity
This paragraph discusses the concept of free fall and the influence of gravity on falling objects. It explains that when two objects are dropped from the same height, they will hit the ground at the same time due to the constant acceleration of gravity (9.8 m/s^2). The example of a 10-gram and a 5-gram metal ball is used to illustrate this point. The paragraph also touches on the role of air resistance, using the demonstration of a brick versus a flat piece of paper to show how air resistance affects the motion of objects with different surface areas. It concludes with a discussion on how crumpling the paper reduces air resistance, allowing it to fall at a similar rate as the brick.
📚 Equations for Constant Speed and Acceleration
The second paragraph introduces the equations used to describe the motion of objects under constant speed and constant acceleration. It differentiates between distance (a scalar quantity) and displacement (a vector quantity). The key equations for constant speed motion are presented, including the formula for displacement over time. The paragraph then transitions to discuss the four fundamental equations for uniformly accelerated motion, which are crucial for solving problems involving free fall and gravitational acceleration. These equations relate final and initial velocities, acceleration, and time, providing a foundation for understanding the dynamics of falling objects.
📉 Calculating Displacement and Distance in Free Fall
This paragraph delves into the application of the previously introduced equations to calculate displacement and distance traveled by an object in free fall. It uses the example of a ball dropped from a cliff to illustrate how to find the speed, velocity, and distance traveled after a specific time interval. The paragraph emphasizes the difference between speed (always positive) and velocity (which includes direction and can be negative). It also demonstrates how to use the formula for displacement when the initial velocity is zero and how to calculate the distance traveled by considering the magnitude of displacement without its sign.
🏙️ Determining the Height of a Building from Free Fall
The focus of this paragraph is on using the principles of free fall to determine the height of a building. It explains how to calculate the distance an object falls by using the formula for displacement under constant acceleration due to gravity. The paragraph provides a step-by-step approach to finding the height of a building by calculating the displacement of a stone dropped from the top. It clarifies the difference between displacement (which can be negative) and the actual height of the building (which is always a positive value).
🕒 Time and Velocity Calculations for a Falling Object
The final paragraph addresses the calculation of the time it takes for an object to fall from a certain height and the velocity it reaches just before impact. Using the example of a rock falling from a 700-meter building, it illustrates how to find the time of fall by rearranging the displacement formula. The paragraph also explains how to calculate the final velocity and speed of the object before it hits the ground, reinforcing the concepts of acceleration due to gravity and the relationship between initial speed, acceleration, time, and final velocity.
Mindmap
Keywords
💡Free Fall
💡Acceleration due to Gravity
💡Air Resistance
💡Velocity
💡Speed
💡Displacement
💡Distance
💡Constant Acceleration
💡Equations of Motion
💡Initial and Final Conditions
💡Scalar and Vector Quantities
Highlights
In a free fall experiment, two balls of different masses will hit the ground at the same time if dropped from the same height and without air resistance.
Air resistance affects objects differently based on their surface area; a flat piece of paper will experience more air resistance than a crumpled one.
The acceleration due to gravity is 9.8 meters per second squared, affecting all objects equally in a vacuum.
Velocity and speed are related but different; velocity is speed with a direction, and it can be negative, while speed is always positive.
The equations for constant acceleration motion are v_final = v_initial + a*t and d = v_initial*t + 0.5*a*t^2.
When solving free fall problems, it's crucial to consider the signs of velocity and displacement based on the direction of motion.
A ball dropped from rest will accelerate at 9.8 m/s^2, and its velocity can be calculated using the formula v_final = v_initial + a*t.
The distance traveled by an object in free fall can be found using the equation d = 0.5*a*t^2, which represents the displacement in the negative y-direction.
For an object thrown downward with an initial speed, the final velocity and displacement can be calculated using the same equations as for a freely falling object.
The height of a structure can be determined by calculating the displacement of an object dropped from its top in free fall.
The time it takes for an object to fall can be found by rearranging the displacement equation to solve for time.
The speed of an object just before impact in free fall is the absolute value of its velocity.
Understanding the relationship between velocity, acceleration, displacement, and time is essential for solving problems involving free fall motion.
In practical scenarios, factors like air resistance can significantly alter the motion of falling objects compared to idealized free fall conditions.
The concept of negative and positive values in physics often relates to direction, with negative typically indicating downward or反向 motion.
Physics equations can be applied to real-world situations, such as calculating the height of a building or the speed of a falling object.
The principles of free fall motion demonstrate the fundamental laws of physics, such as gravity and acceleration.
Transcripts
Browse More Related Video

Do Heavy Objects Actually Fall Faster Than Light Objects? DEBUNKED

College Physics 1: Lecture 9 - Motion With Constant Acceleration
Vertical Projectile Motion: Introduction and Terminology

College Physics 1: Lecture 12 - Projectile Motion

AP Physics 1 - Air Resistance

Gravity Compilation: Crash Course Kids
5.0 / 5 (0 votes)
Thanks for rating: