Standard error of the mean | Inferential statistics | Probability and Statistics | Khan Academy

Khan Academy
26 Jan 201015:15
EducationalLearning
32 Likes 10 Comments

TLDRThe video script discusses the concept of sampling distribution and how it relates to the normal distribution. It explains that as sample size (n) increases, the sampling distribution of the sample mean becomes more normal and has a lower standard deviation. The script introduces the formula for the variance of the sampling distribution as the original variance divided by n, and the standard deviation of the sampling distribution, also known as the standard error of the mean, is the original standard deviation divided by the square root of n. This is demonstrated through a simulation, which confirms the theoretical formula with practical results.

Takeaways
  • 📊 The central concept is that sampling from any distribution, even non-normal ones, and averaging the results will eventually approach a normal distribution.
  • 🔢 The shape of the sampling distribution of the sample mean becomes more normal as the sample size (n) increases.
  • 📈 The standard deviation (or variance) of the sampling distribution of the sample mean decreases as the sample size increases.
  • 🌟 The mean of the sampling distribution of the sample mean is equal to the mean of the original distribution, regardless of the sample size.
  • 🔍 The variance of the sampling distribution of the sample mean can be calculated by dividing the variance of the original distribution by the sample size (n).
  • 📐 The standard deviation of the sampling distribution, also known as the standard error of the mean, is the square root of the variance of the original distribution divided by the square root of the sample size (n).
  • 🧠 The concept is intuitively understood as more trials (larger n) lead to a more accurate estimate of the true mean, hence a smaller standard deviation.
  • 🧩 The video script uses a simulation approach to demonstrate and validate the theoretical concepts through visual evidence.
  • 🔄 The process of taking samples, averaging them, and plotting the average is repeated numerous times to build the sampling distribution of the sample mean.
  • 📝 The script emphasizes the importance of understanding the relationship between the original distribution, sample size, and the resulting sampling distribution.
  • 🎓 The video aims to provide working knowledge first, with the intention of delving into rigorous proofs later on.
  • 🔍 The script concludes with a practical demonstration that confirms the theoretical formulas through empirical evidence from a simulation.
Q & A

  • What is the main concept discussed in the video?

    -The main concept discussed in the video is the relationship between the distribution of sample means and the original distribution from which the samples are drawn, specifically how the sample size (n) affects the standard deviation and normality of the sampling distribution of the sample mean.

  • How does the shape of the sampling distribution of the sample mean change as the sample size increases?

    -As the sample size (n) increases, the sampling distribution of the sample mean becomes more normal, regardless of the shape of the original distribution. This is due to the central limit theorem, which states that the distribution of sample means approaches a normal distribution as the sample size gets larger.

  • What happens to the standard deviation of the sampling distribution of the sample mean as the sample size increases?

    -As the sample size (n) increases, the standard deviation of the sampling distribution of the sample mean decreases. This is because the variance of the sampling distribution is inversely proportional to the sample size, meaning that larger sample sizes result in a tighter distribution around the true mean.

  • What is the formula for the variance of the sampling distribution of the sample mean?

    -The formula for the variance of the sampling distribution of the sample mean is the variance of the original distribution divided by the sample size (n). Mathematically, this is represented as Var(sample mean) = Var(original distribution) / n.

  • What is the standard error of the mean?

    -The standard error of the mean (SEM) is the standard deviation of the sampling distribution of the sample mean. It provides an estimate of how much the sample mean is expected to vary from the true population mean and is calculated by dividing the standard deviation of the original distribution by the square root of the sample size (n).

  • How does the central limit theorem apply to non-normal distributions?

    -The central limit theorem applies to non-normal distributions by stating that the sampling distribution of the sample mean will approach a normal distribution as the sample size increases, even if the original distribution is not normal. This is because the averaging process tends to reduce the impact of the original distribution's shape.

  • What is the significance of the standard error of the mean in statistical analysis?

    -The standard error of the mean is significant in statistical analysis because it provides a measure of the precision of the sample mean as an estimate of the population mean. A smaller SEM indicates that the sample mean is likely to be closer to the true population mean, which in turn increases the confidence in the statistical conclusions drawn from the data.

  • How does the video demonstrate the relationship between the original distribution's variance and the sampling distribution's variance?

    -The video demonstrates this relationship through a series of simulations where different sample sizes (n) are taken from an original distribution with a known variance. The resulting sampling distributions' variances are shown to be proportional to the original variance divided by the sample size, illustrating the inverse relationship between sample size and variance.

  • What is the role of the sample size (n) in determining the precision of the sample mean?

    -The sample size (n) plays a crucial role in determining the precision of the sample mean. As the sample size increases, the precision of the sample mean as an estimate of the population mean also increases. This is because a larger sample size leads to a smaller standard deviation and a tighter sampling distribution, which in turn results in a more accurate estimate of the population mean.

  • How does the video script help in understanding the concept of the central limit theorem?

    -The video script helps in understanding the central limit theorem by providing a clear and detailed explanation of how the sampling distribution of the sample mean evolves as the sample size increases. It uses visual aids and simulations to demonstrate how the distribution becomes more normal and how the standard deviation decreases with increasing sample sizes, reinforcing the theorem's principles.

  • What is the practical implication of the relationship between the original distribution's variance and the sampling distribution's variance?

    -The practical implication of this relationship is that it allows statisticians and researchers to make inferences about population parameters based on sample data. By understanding how the sample size affects the distribution of sample means, they can better design studies and experiments to ensure that their results are reliable and representative of the population of interest.

Outlines
00:00
📊 Understanding Sampling Distributions

This paragraph discusses the concept of sampling distributions, emphasizing that any initial distribution, whether normal or skewed, can be sampled to create a distribution of sample means. It explains that by taking multiple samples of a fixed size (n) and averaging them, the resulting distribution of these averages will approach a normal distribution as the sample size increases. The paragraph also introduces the idea that the standard deviation of this sampling distribution will decrease as the sample size increases, hinting at a formula that relates the standard deviation of the original distribution to the sample size.

05:00
🧠 The Intuition Behind Variance and Sample Size

This paragraph delves into the relationship between the variance of the original distribution and the sample size (n). It suggests that there is a formula to predict the variance of the sampling distribution of the sample mean, which is inversely proportional to the sample size. The speaker explains that the larger the sample size, the smaller the standard deviation of the sampling distribution, and provides an intuitive understanding that more trials (larger n) lead to a more accurate estimate of the true mean. The paragraph also introduces the concept of the standard error of the mean, which is the standard deviation of the sampling distribution of the sample mean.

10:02
📈 Demonstrating the Formula Through Simulation

The speaker uses a simulation to experimentally validate the formula that relates the variance of the original distribution to the sample size. By conducting trials with different sample sizes (n) and plotting the resulting distributions, the paragraph demonstrates that the standard deviation of the sampling distribution decreases as the sample size increases. The results from the simulation align with the theoretical formula, showing that the standard error of the mean is equal to the standard deviation of the original distribution divided by the square root of n.

15:04
🔍 Clarifying the Concept of Standard Error

In this paragraph, the speaker aims to clarify the concept of the standard error of the mean, which is the standard deviation of the sampling distribution of the sample mean. The speaker reiterates that understanding how to calculate the standard error is crucial for grasping the precision of the sample mean as an estimate of the population mean. The paragraph concludes by reinforcing the idea that the variance of the sampling distribution is simply the variance of the original distribution divided by the sample size, and that this understanding can be deepened through further study and practical application.

Mindmap
Keywords
💡distribution
In the context of the video, a distribution refers to the pattern or arrangement of a set of data points. It could be normal or 'crazy,' indicating a range of possible outcomes for a random variable. The video emphasizes that regardless of the initial distribution's shape, taking multiple samples and averaging them will eventually lead to a distribution that approaches a normal distribution, also known as Gaussian distribution, which is symmetric and bell-shaped.
💡sampling
Sampling in this video refers to the process of selecting a subset of data from a larger population. It is a fundamental concept in statistics where one cannot or does not want to analyze the entire population. The video discusses how sampling can lead to an approximation of the population's characteristics, with the accuracy of this approximation improving as the sample size increases.
💡sample mean
The sample mean is the average value of a sample taken from a population. It is used as an estimate for the population's true mean. In the video, the focus is on how the distribution of sample means changes as the sample size (n) changes, showing that the larger the sample size, the closer the sample mean distribution is to a normal distribution and the lower its standard deviation.
💡standard deviation
Standard deviation is a measure of the amount of variation or dispersion in a set of values. A low standard deviation indicates that the values are close to the mean of the distribution, while a high standard deviation indicates that the values are spread out over a wider range. In the video, it is shown that the standard deviation of the sampling distribution of the sample mean decreases as the sample size increases.
💡variance
Variance is the average of the squared differences from the mean and measures how far a set of numbers is spread out. It is closely related to standard deviation, with the difference being that variance has squared units. In the video, the concept of variance is used to explain how the spread of the sampling distribution of the sample mean is related to the original distribution's variance and the sample size.
💡normal distribution
A normal distribution, also known as Gaussian distribution, is a probability distribution that is symmetric about the mean and characterized by a bell-shaped curve. It is important in statistics because it occurs naturally in many phenomena and provides a good approximation for many types of data. The video emphasizes that as the sample size increases, the distribution of sample means approaches a normal distribution.
💡sample size (n)
Sample size (n) refers to the number of individual observations or elements in a sample. In the context of the video, it is the number of instances of a random variable that are taken and then averaged to form a sample mean. The video demonstrates that as the sample size increases, the distribution of these sample means becomes more normal and has a lower standard deviation.
💡standard error of the mean (SEM)
The standard error of the mean (SEM) is a measure of how much the sample mean of a population is likely to vary from one sample to another. It is essentially the standard deviation of the sampling distribution of the sample mean. The smaller the SEM, the more precise the sample mean is as an estimate of the population mean. The video explains that the SEM can be calculated by dividing the standard deviation of the original distribution by the square root of the sample size.
💡probability density function (PDF)
A probability density function (PDF) describes the relative likelihood for this random variable to take on a given value. It is a function that describes the distribution of a continuous random variable and is non-negative for all values of the variable. The video uses the PDF to represent the original distribution from which samples are taken and to illustrate how the distribution of sample means is derived.
💡variance of the mean
The variance of the mean refers to the variance of the sampling distribution of the sample mean. It indicates how much the sample means are likely to vary from the true population mean. The video explains that the variance of the mean is inversely proportional to the sample size, meaning that as the sample size increases, the variance of the mean decreases.
💡experimental proof
An experimental proof in the context of the video refers to the use of simulations or experiments to validate a theoretical concept or formula. Instead of a mathematical proof, the video uses data from simulations to show that the variance of the sampling distribution of the sample mean is indeed equal to the original distribution's variance divided by the sample size.
Highlights

The concept of sampling from a distribution and averaging the results to approach the sampling distribution of the sample mean is introduced.

It is demonstrated that the shape of the sampling distribution of the sample mean can be close to a normal distribution, even if the original distribution is not normal.

The importance of the sample size (n) in determining the standard deviation of the sampling distribution is emphasized; larger sample sizes result in smaller standard deviations.

The mean of the sampling distribution of the sample mean is always equal to the mean of the original distribution, regardless of the sample size.

The relationship between the variance of the original distribution and the variance of the sampling distribution of the sample mean is established, with the latter being the former divided by the sample size (n).

The standard deviation of the sampling distribution of the sample mean is referred to as the standard error of the mean.

The concept of kurtosis and skew is mentioned as future topics for deeper exploration in statistics.

A practical application of the formula for the variance of the sampling distribution of the sample mean is provided through an example with a made-up variance of 20 and sample sizes of 20 and 100.

The inverse relationship between the sample size (n) and the standard deviation of the sampling distribution is visually demonstrated through simulations.

The standard error of the mean is shown to be the square root of the variance of the original distribution divided by the square root of the sample size (n).

The transcript provides a clear explanation of the difference between the sample mean and the mean of the sampling distribution of the sample mean.

The transcript emphasizes the value of experimental proofs and simulations in understanding statistical concepts, suggesting that rigorous mathematical proofs can come later.

The process of deriving the formula for the standard error of the mean is explained, highlighting the intuitive understanding of the relationship between n and standard deviation.

The transcript provides a practical example of how to apply the formula for the standard error of the mean to real data, with a demonstration of how close the experimental results are to the theoretical values.

The transcript concludes with a reiteration of the main points, reinforcing the understanding of how the sample size affects the standard error of the mean and the importance of this concept in statistics.

Transcripts

Browse More Related Video

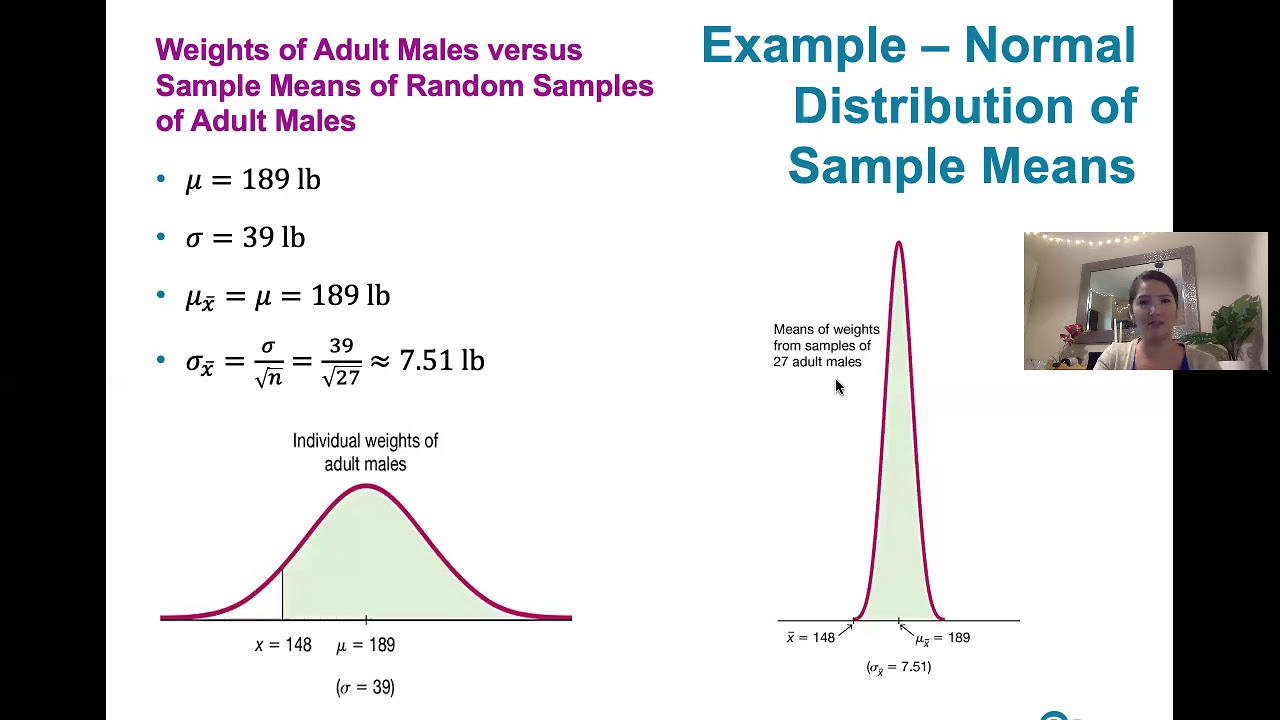
6.4.1 The Central Limit Theorem - What the Central Limit Theorem Says and What It Doesn't Say

The Sampling Distribution of the Sample Mean

Sampling distribution of the sample mean 2 | Probability and Statistics | Khan Academy

Standard Error of the Mean: Concept and Formula | Statistics Tutorial #6 | MarinStatsLectures

Introduction to the t Distribution (non-technical)

Central Limit Theorem & Sampling Distribution Concepts | Statistics Tutorial | MarinStatsLectures

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
StatisticsSampling DistributionStandard DeviationVarianceProbabilityData AnalysisMathematical ConceptsEducational ContentStatistical InferenceRandom Variables