Video 36 - Covariant Derivative Properties

Tensor Calculus

5 Sept 202320:01

EducationalLearning

32 Likes 10 Comments

TLDRThis video delves into the properties of the covariant derivative in tensor calculus, focusing on the sum rule, which states that the covariant derivative of a sum of tensors equals the sum of their individual derivatives. It also establishes the product rule's applicability to tensors of any rank, similar to partial derivatives. Furthermore, the video explores the commutativity property of the covariant derivative, highlighting its validity in flat manifolds but noting its absence in curved spaces. These properties underscore the covariant derivative's role as a generalized partial derivative, applicable in various coordinate systems.

Takeaways

📚 The video discusses important properties of the covariant derivative in tensor calculus.
🔢 The 'sum rule' states that the covariant derivative of a sum of tensors is equal to the sum of the covariant derivatives of the individual tensors.
📐 The 'product rule' is shown to apply to tensors of any rank, not just vector components, and is analogous to the regular product rule in calculus.
🔄 The 'commutativity property' explains that the order of taking covariant derivatives with respect to different variables does not affect the result, a property that holds true in flat spaces.
📉 The commutativity property is not universally applicable; it fails in non-flat or curved manifolds, leading to a nonzero result.
📝 The video script uses specific examples to illustrate these properties, but the principles are applicable to tensors of any rank or index structure.
🧩 The covariant derivative is a linear operation, which means scalar factors can be factored out and distributed over sums or differences of tensors.
🔍 The script emphasizes that the properties of the covariant derivative mirror those of the partial derivative, including sum rule, product rule, and commutativity.
🔍 The covariant derivative is a generalization of the partial derivative, applicable to both flat (Euclidean) and curvilinear coordinates.
🚀 The video foreshadows the introduction of the 'metric compatibility' property in the next video, which is unique to the covariant derivative.
📚 The script concludes by reinforcing that the properties of the covariant derivative are fundamental to understanding tensor calculus in the context of both flat and curved spaces.

Q & A

What is the sum rule in the context of covariant derivatives?
-The sum rule states that the covariant derivative of a sum of tensors is equal to the sum of the covariant derivatives of each of those tensors individually, provided that the tensors have consistent index structures.
Why is the covariant derivative considered a linear operation?
-The covariant derivative is considered a linear operation because it satisfies the properties of additivity and homogeneity, meaning it can factor out scalar factors and distribute over sums.
How does the product rule for tensors of any rank differ from the one introduced in video 34?
-In video 34, the product rule was introduced for simple vector components (rank one tensors). The script demonstrates that the product rule also applies to tensors of any rank, showing an example with a second-rank tensor multiplied by a third-rank tensor.
What does it mean for the covariant derivative to be commutative?
-The commutativity of the covariant derivative means that the order in which covariant derivatives are taken with respect to different variables does not affect the result, i.e., the derivative with respect to J first then I is the same as with respect to I first then J.
Under what conditions is the commutativity property of the covariant derivative not valid?
-The commutativity property of the covariant derivative is not valid in non-flat manifolds or spaces that are curved. It only holds true for flat spaces, such as Euclidean spaces.
What is the significance of the commutativity property in tensor calculus?
-The commutativity property is significant because it simplifies calculations and proofs in tensor calculus. However, its violation in non-flat spaces is crucial for understanding the curvature of space and is a key topic in the study of non-Euclidean geometries.
Why is it important to demonstrate that the product rule works for tensors of any rank?
-Demonstrating that the product rule works for tensors of any rank is important because it confirms the general applicability of the rule, allowing for more complex tensor operations and calculations in various coordinate systems.
What does the script imply about the relationship between partial derivatives and covariant derivatives?
-The script implies that the properties of partial derivatives, such as the sum rule, product rule, and commutativity, carry over to covariant derivatives, which can be thought of as a generalized form of partial derivatives that apply to both flat and curvilinear coordinates.
What is the next property of the covariant derivative that will be introduced in the following video?
-The next property to be introduced in the following video is the metric property, which is unique to covariant derivatives.
How does the script illustrate the generalizability of the sum rule, product rule, and commutativity across different tensor ranks and index structures?
-The script uses specific examples with second-rank and third-rank tensors to illustrate the properties. It emphasizes that these properties are not limited to these examples but are applicable to tensors of any rank or index structure, as long as the index structures are consistent.

Outlines

00:00

📚 Sum Rule and Linearity of Covariant Derivative

This paragraph introduces the sum rule of the covariant derivative, which states that the derivative of a sum of tensors is equal to the sum of their individual derivatives. The rule is demonstrated using second-rank tensors with consistent index structures. The process involves taking the partial derivative and applying the Christoffel symbols, resulting in the sum of the covariant derivatives of each tensor. The paragraph also highlights the linearity of the covariant derivative, meaning it can distribute over scalar multiplication and works for any number of terms, regardless of tensor rank or index structure.

05:03

🔍 Product Rule Application for Tensors of Any Rank

The second paragraph delves into the product rule for the covariant derivative, extending the rule beyond simple vector components to tensors of any rank. The example provided involves a second-rank tensor multiplied by a third-rank tensor. The paragraph demonstrates that applying the product rule yields the same result as taking the covariant derivative directly. The process involves expanding the covariant derivatives and showing that certain terms cancel out due to index contractions, leading to the conclusion that the product rule is valid for tensors of any rank.

10:05

🔄 Commutativity of Covariant Derivatives in Flat Spaces

The third paragraph explores the commutativity property of the covariant derivative, questioning whether the order of differentiation with respect to different variables affects the outcome. It is established that in Cartesian coordinates, where the covariant derivative is equivalent to the partial derivative, the order does not matter due to the properties of second partial derivatives. This leads to the conclusion that the covariant derivative is commutative in flat spaces, such as Euclidean space. However, the paragraph foreshadows that this property does not hold in non-flat manifolds, where the commutator of covariant derivatives can yield a non-zero result.

15:06

📘 Recap of Covariant Derivative Properties in Tensor Calculus

The final paragraph summarizes the key properties of the covariant derivative discussed in the video: the sum rule, the product rule, and commutativity. It emphasizes that these properties apply to tensors of any rank or index structure and are analogous to those of the partial derivative. The paragraph also reiterates that while the commutativity property is true for flat manifolds, it does not hold for curved spaces, which will be explored in future videos. The covariant derivative is presented as a generalized partial derivative, applicable to both Cartesian and curvilinear coordinates, with a unique property to be introduced in the next video.

Mindmap

Keywords

💡Covariant Derivative

The covariant derivative is a generalization of the partial derivative that is used in tensor calculus to differentiate tensors in a way that is invariant under coordinate transformations. It is essential in the study of curved spaces and manifolds. In the video, the covariant derivative is analyzed for its properties, such as the sum rule, product rule, and commutativity, illustrating its behavior with different tensor structures.

💡Sum Rule

The sum rule in the context of the covariant derivative states that the derivative of a sum of tensors is equal to the sum of the derivatives of each tensor individually. This property is a direct consequence of the linearity of the covariant derivative and is demonstrated in the script with an example involving tensors with consistent index structures.

💡Tensor

A tensor is a mathematical object that generalizes scalars, vectors, and higher-dimensional arrays. It is characterized by its rank, which corresponds to the number of indices it has. In the video, tensors of various ranks are used to illustrate the properties of the covariant derivative, showing how these properties apply universally regardless of the tensor's rank or index structure.

💡Product Rule

The product rule for the covariant derivative is analogous to the product rule in calculus, stating that the derivative of a product of two tensors is equal to the derivative of the first tensor times the second, plus the first tensor times the derivative of the second. The video extends this rule beyond simple vector components to tensors of any rank, showcasing its universal applicability.

💡Commutativity

Commutativity in the context of the covariant derivative refers to the property that the order in which covariant derivatives are taken with respect to different variables does not affect the result. The video script discusses this property, noting its validity in flat spaces like Euclidean space but its potential violation in curved spaces.

💡Partial Derivative

A partial derivative is a derivative of a function of multiple variables with respect to one of those variables, while the others are held constant. In the video, the properties of the covariant derivative are related back to those of the partial derivative, emphasizing that the covariant derivative is a generalized form of the partial derivative that accounts for curvature in space.

💡Euclidean Space

Euclidean space is a mathematical setting characterized by flat geometry, where the usual rules of Euclidean geometry apply. The video mentions Euclidean space as an example of a flat manifold where the commutativity property of the covariant derivative holds true.

💡Manifold

A manifold is a topological space that locally resembles Euclidean space. It is used in differential geometry to model spaces that may be curved or have other complex properties. The script discusses how the properties of the covariant derivative can vary depending on whether the manifold is flat or curved.

💡Index Structure

In the context of tensors, the index structure refers to the arrangement of covariant and contravariant indices that a tensor possesses. The video script uses the index structure to illustrate how the covariant derivative operates on tensors and how the sum rule applies to tensors with consistent index structures.

💡Distributive Property

The distributive property is a fundamental property of arithmetic that states that multiplication distributes over addition. In the video, this property is applied to the covariant derivative, allowing for the expansion of expressions involving sums of tensors under the derivative.

💡Contravariant and Covariant Indices

In tensor calculus, contravariant and covariant indices are used to distinguish between the types of indices a tensor may have. Contravariant indices increase the dimension of a space, while covariant indices decrease it. The video script uses these concepts to explain how the covariant derivative is applied to tensors with specific index structures.

Highlights

Introduction to the covariant derivative and its important properties in tensor calculus.

Analysis of the sum rule for the covariant derivative, showing its linearity and application to tensors with consistent index structures.

Demonstration of the covariant derivative's distributive property over algebraic expressions.

Explanation of how the covariant derivative of a sum of tensors equals the sum of their individual covariant derivatives.

Illustration of the product rule for tensors of any rank, extending the rule beyond simple vector components.

Verification that applying the product rule to tensor products yields the same result as direct covariant differentiation.

Discussion on the commutativity property of the covariant derivative and its implications for different coordinate systems.

Clarification that the commutativity property holds true only for flat manifolds, such as Euclidean spaces.

Introduction of the concept that the covariant derivative is a generalized form of the partial derivative, applicable to both flat and curvilinear coordinates.

Highlighting the fact that the covariant derivative inherits the sum rule, product rule, and commutativity from the properties of partial derivatives.

Foreshadowing the non-commutativity of the covariant derivative in non-Euclidean manifolds, indicating a key topic for future study.

Emphasis on the universality of the discussed properties, applicable to tensors of any rank or index structure.

The covariant derivative's role in tensor calculus as a fundamental operation with unique properties.

The upcoming introduction of the metric property of the covariant derivative, which is unique to this operation.

Reinforcement of the understanding that the properties of the covariant derivative are a natural extension of the familiar properties of partial derivatives.

Final summary of the video's content, emphasizing the significance of the sum rule, product rule, and commutativity in the context of tensor calculus.

Transcripts

Browse More Related Video

Video 73 - Surface Covariant Derivative Properties

Video 37 - Metrinilic Property - Part 1

Tensor Calculus Lecture 6c: The Covariant Derivative 2

Tensor Calculus 17.5: Covariant Derivative (Component Definition) - Optional

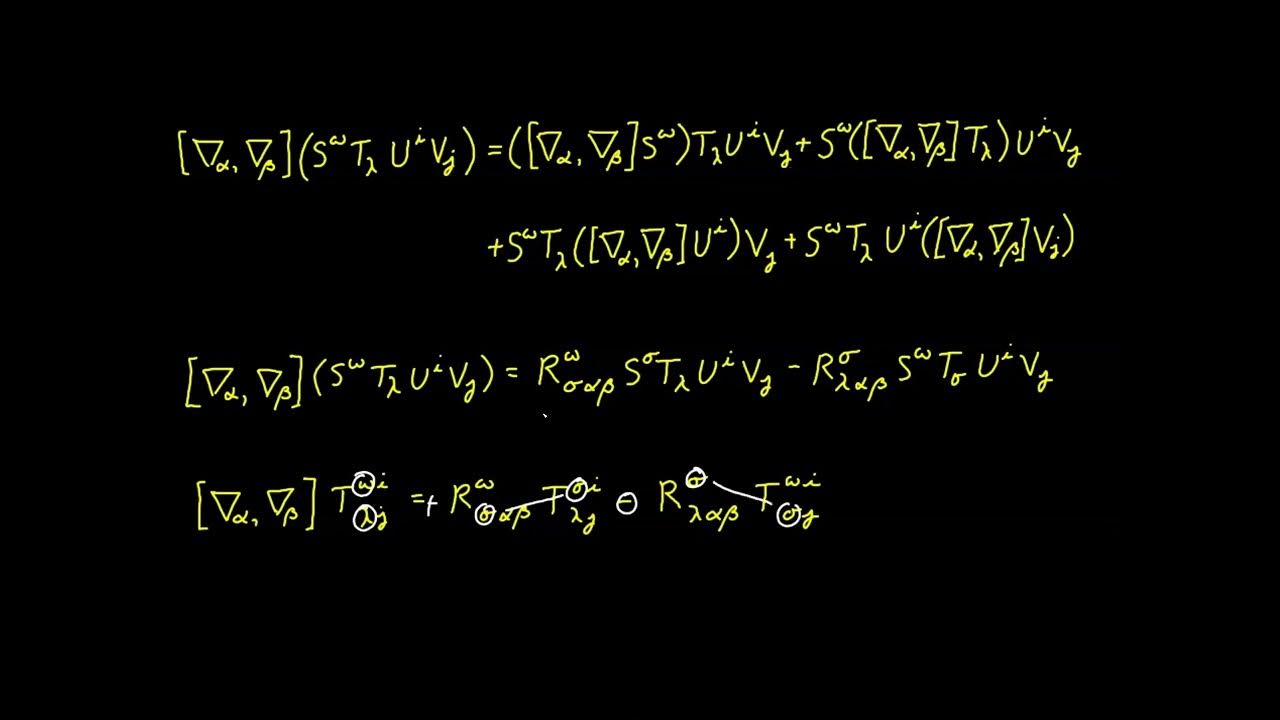
Video 85 - Commutation for Higher Rank Tensors

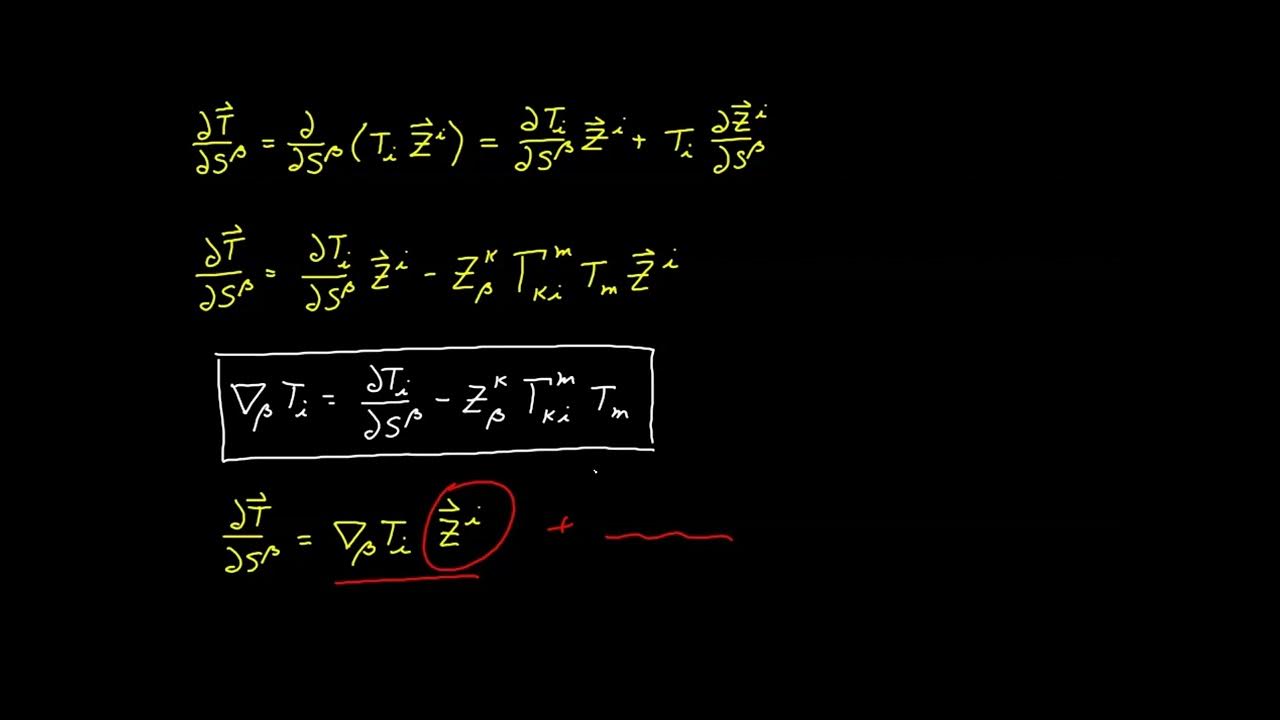
Video 72 - Surface Covariant Derivative for Non Tangent Vectors